
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Correct answer is d
In parallel.
Answers: 3.1a, 3.2c, 3.3b, 3.4d, 3.5c, 3.6a, 3.7d, 3.8b, 3.9c, 3.10b,d.
CHAPTER 4 Circuit Theorems
4.1The current through a branch in a linear network is 2 A when the input source voltage is 10 V. If the voltage is reduced to 1 V and the polarity is reversed, the current through the branch is:
(b) −0.2
4.2For superposition, it is not required that only one independent source be considered at a time; any number of independent sources may be considered simultaneously.
(a) True
4.3The superposition principle applies to power calculation.
(b) False
4.4Refer to Fig. 4.67. The Thevenin resistance at terminals a and b is:
(d) 4Ω

4.5The Thevenin voltage across terminals a and b of the circuit in Fig. 4.67 is:
(b) 40 V
4.6The Norton current at terminals a and b of the circuit in Fig. 4.67 is:
(a) 10 A
4.7The Norton resistance RN is exactly equal to the Thevenin resistance RTh.
(a) True
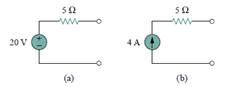
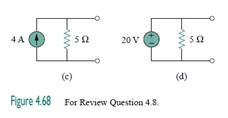
4.8Which pair of circuits in Fig. 4.68 are equivalent?
(c) a and c
4.9A load is connected to a network. At the terminals to which the load is connected, RTh = 10 Ohm and VTh = 40 V. The maximum power supplied to the load is:
(c) 40 W
4.10The source is supplying the maximum power to the load when the load resistance equals the source resistance.
(b) False
Answers: 4.1b, 4.2a, 4.3b, 4.4d, 4.5b, 4.6a, 4.7a, 4.8c, 4.9c, 4.10b.
CHAPTER 5 Operational Amplifiers
5.1The two input terminals of an op amp are labeled as:
(c) inverting and noninverting.
.
5.2For an ideal op amp, which of the following
(c) The current from the output terminal is zero.
(d) The input resistance is zero.
5.3For the circuit in Fig. 5.39, voltage vo is:
(b) −5 V
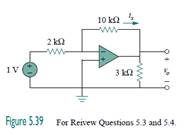
5.4For the circuit in Fig. 5.39, current ix is:
(b) 0.5 A
5.5If vs = 0 in the circuit of Fig. 5.40, current io is:
(a) −10 A
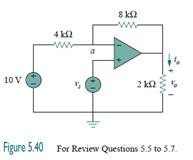
5.6If vs = 8 V in the circuit of Fig. 5.40, the output voltage is:
(c) 4 V
5.7Refer to Fig. 5.40. If vs = 8 V, voltage va is:
(d) 8 V
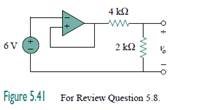
5.8The power absorbed by the 4-k_ resistor in Fig.
5.41 is:
(b) 4 mW
5.9Which of these amplifiers is used in a digital-to-analog converter?
(c) summer
5.10Difference amplifiers are used in:
(a) instrumentation amplifiers
(f) subtracting amplifiers
Answers: 5.1c, 5.2c,d, 5.3b, 5.4b, 5.5a, 5.6c, 5.7d, 5.8b, 5.9c, 5.10a,f.
CHAPTER 6 Capacitors andInd uctors
6.1What charge is on a 5-F capacitor when it is connected across a 120-V source?
(a) 600 C
6.2Capacitance is measured in:
(d) farads
6.3When the total charge in a capacitor is doubled, the energy stored:
(d) is quadrupled
6.4Can the voltage waveform in Fig. 6.42 be associated with a capacitor?
(b) No

6.5The total capacitance of two 40-mF series-connected capacitors in parallel with a 4-mF capacitor is:
(c) 24 mF
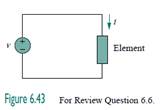
6.6In Fig. 6.43, if i=cos 4t and v=sin 4t , the element is:
(b) a capacitor
6.7A 5-H inductor changes its current by 3 A in 0.2 s. The voltage produced at the terminals of the inductor is:
(a) 75 V
6.8If the current through a 10-mH inductor increases from zero to 2 A, how much energy is stored in the inductor?
(b) 20 mJ
6.9Inductors in parallel can be combined just like resistors in parallel.
(a) True


Answers: 6.1a, 6.2d, 6.3d, 6.4b, 6.5c, 6.6b, 6.7a, 6.8b, 6.9a, 6.10d.
CHAPTER 7 First-Order Circuits
7.1An RC circuit has R = 2 Ωand C = 4 F. The time constant is:
(d) 8 s
7.2The time constant for an RL circuit with R = 2 Ωand L = 4 H is:
(b) 2 s
7.3A capacitor in an RC circuit with R = 2 Ω and C = 4 F is being charged. The time required for the capacitor voltage to reach 63.2 percent of its steady-state value is:
(c) 8 s
7.4An RL circuit has R = 2 Ω and L = 4 H. The time needed for the inductor current to reach 40 percent of its steady-state value is:
(b) 1 s
7.5In the circuit of Fig. 7.79, the capacitor voltage just before t = 0 is:
(d) 4 V
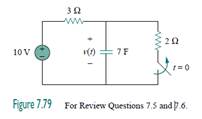
7.6In the circuit of Fig. 7.79, v(∞) is:
(a) 10 V
7.7For the circuit of Fig. 7.80, the inductor current just before t = 0 is:
(c) 4 A

7.8In the circuit of Fig. 7.80, i(∞) is:
(e) 0 A
7.9If vs changes from 2 V to 4 V at t = 0, we may express vs as:
(c) 2u(−t) + 4u(t) V
(d) 2 + 2u(t) V
7.10The pulse in Fig. 7.110(a) can be expressed in terms of singularity functions as:
(b) 2u(t) − 2u(t − 1) V
Answers: 7.1d, 7.2b, 7.3c, 7.4b, 7.5d, 7.6a, 7.7c, 7.8e, 7.9c,d, 7.10b.
CHAPTER 8 Second-Order Circuits
8.1For the circuit in Fig. 8.58, the capacitor voltage at t = 0− (just before the switch is closed) is:
(a) 0 V
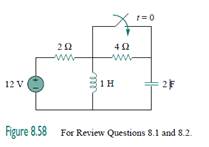
8.2 For the circuit in Fig. 8.58, the initial inductor current (at t = 0) is:
(c) 6 A
8.3When a step input is applied to a second-order circuit, the final values of the circuit variables are found by:
(b) Replacing capacitors with open circuits and inductors with closed circuits.

Correct answer is d
8.5In a series RLC circuit, setting R = 0 will produce:
(d) an undamped response
8.6A parallel RLC circuit has L = 2 H and C = 0.25 F. The value of R that will produce unity damping factor is:
(c) 2 Ohm
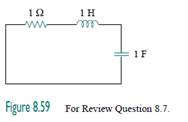
8.7Refer to the series RLC circuit in Fig. 8.59. What kind of response will it produce?
(b) underdamped
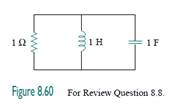
8.8Consider the parallel RLC circuit in Fig. 8.60. What type of response will it produce?
(b) underdamped
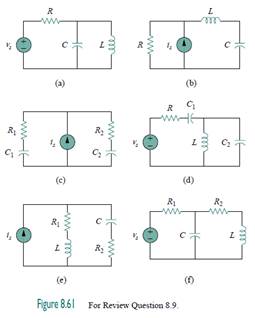
8.9Match the circuits in Fig. 8.61 with the following items:
(i) first-order circuit – c
(ii) second-order series circuit – b, e
(iii) second-order parallel circuit – a
(iv) none of the above – d, f
8.10In an electric circuit, the dual of resistance is:
(a) conductance
Answers: 8.1a, 8.2c, 8.3b, 8.4d, 8.5d, 8.6c, 8.7b, 8.8b, 8.9 (i)-c, (ii)-b,e, (iii)-a, (iv)-d,f, 8.10a.
CHAPTER 9 Sinusoids and Phasors
9.1Which of the following is not a right way to express the sinusoid Acos ωt?
(d) Asin(ωt − 90°)
9.2A function that repeats itself after fixed intervals is said to be:
(c) periodic
9.3Which of these frequencies has the shorter period?
(b) 1 kHz
9.4If v1 = 30 sin(ωt + 10°) and v2 = 20 sin(ωt + 50°),
which of these statements are true?
(b) v2 leads v1
(d) v1 lags v2
9.5The voltage across an inductor leads the current through it by 90°.
(a) True
9.6The imaginary part of impedance is called:
(e) reactance
9.7The impedance of a capacitor increases with increasing frequency.
(b) False
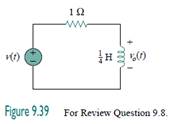
9.8At what frequency will the output voltage vo(t) in Fig. 9.39 be equal to the input voltage v(t)?
(d) ∞rad/s
9.9A series RC circuit has VR = 12 V and VC = 5 V. The supply voltage is:
(c) 13 V
9.10A series RCL circuit has R = 30 Ω, XC =−50 Ω, and XL = 90 Ω. The impedance of the circuit is:
(b) 30 + j40 Ω
Answers: 9.1d, 9.2c, 9.3b, 9.4b,d, 9.5a, 9.6e, 9.7b, 9.8d, 9.9c, 9.10b.
CHAPTER 10 Sinusoidal Steady-State Analysis
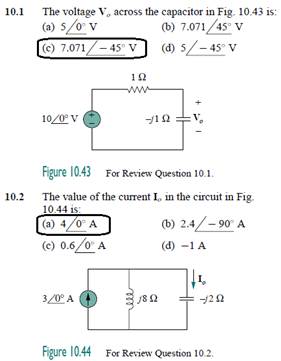
10.3Using nodal analysis, the value of Vo in the circuit of Fig. 10.45 is:
(d) 24 V
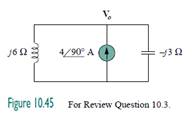
10.4In the circuit of Fig. 10.46, current i(t) is:
(a) 10 cos t A
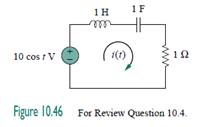
10.5Refer to the circuit in Fig. 10.47 and observe that the two sources do not have the same frequency. The current ix (t) can be obtained by:
(b) the superposition theorem
(
10.6For the circuit in Fig. 10.48, the Thevenin impedance at terminals a-b is:
(c) 0.5 + j0.5 Ω
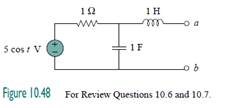
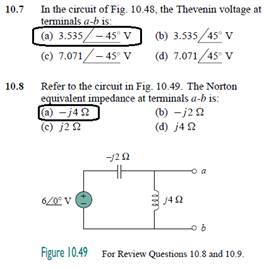

10.10PSpice can handle a circuit with two independent sources of different frequencies.
(b) False
Answers: 10.1c, 10.2a, 10.3d, 10.4a, 10.5b, 10.6c, 10.7a, 10.8a, 10.9d, 10.10b.
Date: 2015-12-11; view: 10530
| <== previous page | | | next page ==> |
| AMENDMENTS TO THE CONSTITUTION OF THE UNITED STATES | | | THE HISTORY OF THEORETICAL GRAMMAR DEVELOPMENT |