
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
How many different 6-letter arrangements can be formed using the letters in the word
ABSENT, if each letter is used only once?
a. 6
b. 36
c. 720
d. 46,656
54. Evaluate 1!+2!+3!
Correct Answer: 1 + 2 + 6 = 9
55. A pair of dice is rolled. A possible event is rolling a multiple of 5. What is the probability of the complement of this event?
a. 2/36
b. 12/36
c. 29/36
d. 32/36
Explanation: Multiples of 5: 5, 10
There are 7 ways to roll a 5 or 10.
P(multiple of 5)=7/36
P(complement)=1-7/36=29/36
56. Your state issues license plates consisting of letters and numbers. There are 26 letters and the letters may be repeated. There are 10 digits and the digits may be repeated. How many possible license plates can be issued with two letters followed by three numbers?
a. 25,000
b. 67,600
c. 250,000
d. 676,000
26*26*10*10*10 = 676,000
57. A random variable X has the cumulative distribution function
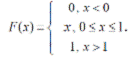 Compute the expectation of X.
Compute the expectation of X.
To find E[X], we first find the PDF by differentiating the above CDF.
X – 1 for 1 <= x <= 2
0 otherwise
Correct Answer: sqrt(7/12) or 0.7637 ?????
58. A fair coin is thrown in the air four times. If the coin lands with the head up on the first three tosses, what is the probability that the coin will land with the head up on the fourth toss?
a. 0
b. 1/16
c. 1/8
d. 1/2
Explanation: The fourth toss is independent of the first three tosses - it has nothing to do with the first three tosses. Therefore, the probability remains one out of two.
59. A movie theater sells 3 sizes of popcorn (small, medium, and large) with 3 choices of toppings (no butter, butter, extra butter). How many possible ways can a bag of popcorn be purchased?
a. 1
b. 3
c. 9
d. 27
Explanation: 3 x 3 = 9
60. A random variable Y has the following distribution:
Y | -1 0 1 2
P(Y) | 3C 2C 0.4 0.1
The value of the constant C is:
a. 0.10
b. 0.15
c. 0.20
d. 0.25
e. 0.75
61. A random variable X has a probability distribution as follows:
X | 0 1 2 3
P(X) | 2k 3k 13k 2k
Then the probability that P(X < 2.0) is equal to
(a) 0.90
(b) 0.25
(c) 0.65
(d) 0.15
(e) 1.00
62. Which one of these variables is a continuous random variable?
The time it takes a randomly selected student to complete an exam.
The number of tattoos a randomly selected person has.
The number of women taller than 68 inches in a random sample of 5 women.
The number of correct guesses on a multiple choice test.
The number of 1’s in N rolls of a fair die
63. Heights of college women have a distribution that can be approximated by a normal curve with a mean of 65 inches and a standard deviation equal to 3 inches. About what proportion of college women are between 65 and 67 inches tall?
A. 0.75
B. 0.50
C. 0.25
D. 0.17
64. The probability is p = 0.80 that a patient with a certain disease will be successfully treated with a new medical treatment. Suppose that the treatment is used on 40 patients. What is the "expected value" of the number of patients who are successfully treated?
A. 40 B. 20 C. 8 D. 32
65. A medical treatment has a success rate of 0.8. Two patients will be treated with this treatment. Assuming the results are independent for the two patients, what is the probability that neither one of them will be successfully cured?
A. .5
B. .36
C. .2
D. .04 (this is (1 – .8)(1 – .8) = (.2)(.2) = .04)
Date: 2015-12-11; view: 3712
| <== previous page | | | next page ==> |
| The table below shows the probability mass function of a random variable X. | | | Scientific Library of Al-Farabi Kazakh National University |