The table below shows the probability mass function of a random variable X.

Xi 0 x2 5

pi 0.1 0.2 0.7 If E[X]=5,5 find the value of x2.

0*0.1+x₂*0.2+5*0.7=5.5 ;

0.2*x₂=5.5-3.5;

x₂ = 10

The probability of machine failure in one working day is equal to 0.01. What is the probability that the machine will work without failure for 5 days in a row.

P(fail for 1 day)=0.01 P(not fail)=0.99 P(not fail for 5 days)=0.99⁵=0.9509

The cumulative distribution function of a discrete random variable X is given by

Find P{3<X<9}.

0.6

22. A fair die is rolled three times. A random variable X denotes the number of occurrences of 6’s. What is the probability that X will have the value which is not equal to 0.

11/136

23. Find the expectation of a random variable X if the cdf

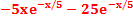
24. Compute the mean for the continuous random variable X with probability density function

1/3

25. If the variance of a random variable X is given Var(X)=3. Then Var(2X) is

26. Indicate the expectation of a Poisson random variable X with parameterl .

E[x]=λ

27. Indicate the variance of a Poisson random variable X with parameterl .

Var(X) = λ

Indicate the formula of the conditional expectation.

29. The table below shows the pmf of a random variable X. What is the Var(X)?

X -2 1 2

Р 0,1 0,6 0,3

1,2

The lifetime of a machine part has a continuous distribution on the interval (0, 40) with

probability density function Calculate the probability that the lifetime of the machine part is less than 6.

15/32 = 0.47

The lifetime of a machine part has a continuous distribution on the interval (0, 40) with

probability density function . Calculate the probability that the lifetime of the machine part is less than 5.

5/12 = 0.42

32. If Var(X)=2, find Var(-3X+4).

33. The table below shows the pmf of a random variable X. Find E[x] and Var(X).

X -1 0 1

P 0.2 0.3 0.5

E[x]=0.3

Var(x) =-0.2

What kind of distribution is given by the density function

(-¥< x <¥)?

Normal RV

If a fair die is tossed twice, the probability that the first toss will be a number less than 4 and the second toss will be greater than 4 is

0.12 ???

1/6 ???

A class consists of 490 female and 510 male students. The students are divided according to their marks

Passed Did not

Pass

Female 430 60

Male 410 100

If one person is selected randomly, the probability that it did not pass given that it is female is:

(a) 0.06 (b) 0.12 (c) 0.41 (d) 0.81 (e) none of the preceding

A - ’pass’, Ac - did not pass, F - female, Fc- ’not female’=male.

To compute: P(Ac|F) =P(Ac∩ F)P(F)= (60/1000) / (490/1000) = 0.12

37. Marks on a Chemistry test follow a normal distribution with a mean of 65 and a standard deviation of 12. Approximately what percentage of the students have scores below 50?

10.56%

38. Suppose the test scores of 600 students are normally distributed with a mean of 76 and standarddeviation of 8. The number of students scoring between 70 and 82 is:

328.08

39. The distribution of weights in a large group is approximately normally distributed. The mean is80 kg. and approximately 68% of the weights are between 70 and 90 kg. The standarddeviation of the distribution of weights is equal to:

10.1

40. If the probability density function of a continuous random variable X is

thenP{0 £ x £1.5} is

0.5625

41. Let X be a continuous random variable with density function

Calculate the expected value of X.

Date: 2015-12-11; view: 2352