
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Introduction to Polymer Science and Technology
Microstructure
|
| Scattered Light |
| SALS pattern |
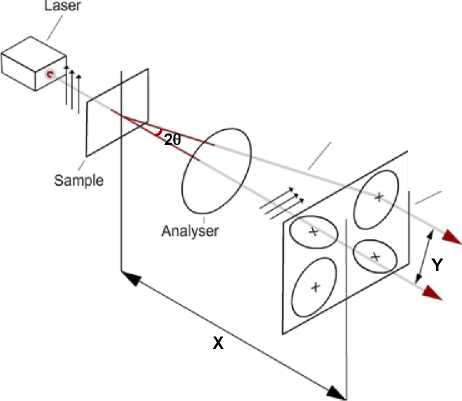
Figure 4.6Illustration of SALS set up
Spherulite radius can be measured using the SALS set up shown in Figure 4.6: polarised monochromatic light of known wavelength, X, impinges on a sample of film material, the light gets scattered by the spherulites and the scattered light is passed through an analyser and is captured on a photographic plate, producing a four-lobed clover leaf pattern. The average spherulite radius, R, can be calculated from the polar scattering angle, 8, using the relationship given below. The scattering angle is determined using the distances of X and Y shown in the figure. X is the axial distance between the sample and the photographic plate, and Y is half the distance between the peaks of the diagonal lobes of the SALS pattern.
R « 1.02 X1 [n sin(6)],
where, 26 = tan"1 (Y/X).
"1Laser jt- Extruddfe
j_ [ Camera
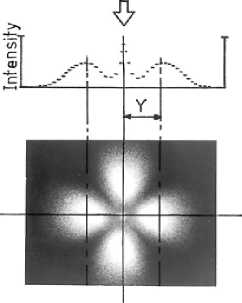
Figure 4.7A schematic of on-line spherulite size monitoring for film extrudate (source: Akay & Barkley (1984))
Introduction to Polymer Science and Technology Microstructure
The measurement of the smaller morphological unit of lamellae relies on small angle X-ray scattering (SAXS) using a suitable X-ray diffractometer. The stacks of lamellae present in spherulites produce a circular SAXS pattern shown in Figure 4.8. Although such a photographic output shows the concept well, the equipment produces digital data in the form of plots of x-ray intensity vs. diffraction angle, 28. The scattering is caused by the densely packed lamellae rather than the non-crystalline inter-lamellar regions. SAXS pattern therefore enables the measurement of'long period', which represents the thickness of both a lamella and an inter-lamellar space. From the radius of the SAXS pattern and the distance between the specimen and the x-ray film (detector), the long period can be calculated using Braggs equation
nA, = 2d (sin6)
where, 'd' is the spacing between adjacent crystal planes (in this case the long period. L) and 8 is the Bragg angle (note that 28 is known as the diffraction angle).
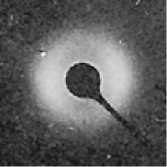
Figure 4.8Generation of a SAXS pattern from lamellae
4.3 Degree of crystallinity
The long chain molecules in crystalline thermoplastic polymers manage to pack closely together in some regions, producing lamellae. However, the entanglements of the long molecules hinders this orderly packing in other regions giving rise to amorphous (meaning without morphology/shape) structure, as in tie molecules in the inter-lamellar spaces. Accordingly the crystalline polymers such as PEs, PP and nylons are more appropriately also referred to as semi-crystalline. This structural mix is exhibited within a spherulite, which consists of radially-grown crystalline fibrillar lamellae and the amorphous tie molecules that are irregularly entangled as delineated in Figure 4.4.
The tendency of a polymer to crystallise, the magnitude of crystallinity and the stability of crystallisation is dictated by a number of factors, including the degree of close packing and/or by the presence of intermolecular forces.The size and the stereoregularity of the side groups, pendant from the main backbone of the macromolecule, is a major factor in the level of packing between the neighbouring polymer chains. Small pendant groups and tacticity favour close packing of the molecules and therefore increase crystallinity.
The rate of cooling of the melt for solidification also influences the degree of crystallinity:during crystallization, upon cooling through melting point, polymers become highly viscous. Time is required for random and entangled chains to become ordered, slow cooling allows time for molecules to arrange themselves into an orderly structure. Intermolecular forces, such as H-bonding, also encourage crystallinity and more importantly leads to increased stability of the crystalline regions. This is why crystalline structure in Nylon 6,6 is much more stable (Figure 4.9) compared with other aliphatic thermoplastics such as PEs and PP, and hence exhibits a much higher melting point.
Date: 2015-12-11; view: 902
| <== previous page | | | next page ==> |
| Introduction to Polymer Science and Technology Polymer processing | | | Introduction to Polymer Science and Technology |