What is the Parabola?

The focus, directrix of the parabola.

Find equation of a line equidistant from the point А(2; 1) and a line x=0.

26. Sets. Operations with sets.

The numeric set.

Let 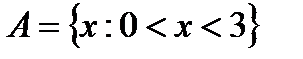and 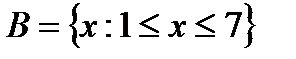are numeric sets. Find the union, intersection, and difference (B\A) of them.

27. The concept of the function.

The event and odd functions.

Roundedness function.

Find out even (odd) function .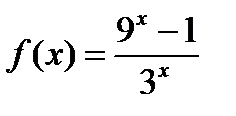

28. Monotonicity functions.

Inverse function.

Find the inverse of this function 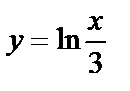. Construct the graphs given and inverse functions.

29. Given a graph of the function y = f (x). Describe how to construct a graph of the following functions: y=f(х)+b, y=f(х+а), y=|f(х)| .

Draw the graph of the function у = -x²+2x-3 and graphics above cases.

30. Given a graph of the function y = f (x). Describe how to construct a graph of the following functions: y=kf(х), y=f(kх), y=f(|х|) .

Draw the graph of the function у = -x²+2x+3 and graphics above cases.

31. Given a graph of the function y = f (x). Describe how to construct a graph of the following functions: y=-f(х), y=f(-х), y=f(|х|) .

Draw the graph of the function у = -x²-2x+3 and graphics above cases.

32. Limes of functions.

Its properties.

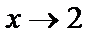Calculate the limit of function as and .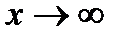

33. The first remarkable limit.

Its consequence.

Calculate the limit .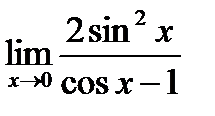

34. The second remarkable limit.

Its consequence.

Calculate the limit .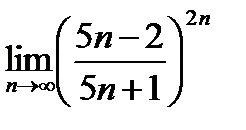

35. Infinitely small and infinitely large functions.

Communication between the infinitely small and infinitely large functions.

When the function 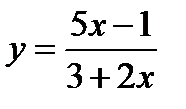is infinitely small?

And when the infinite?

36. Continuity of function y = f (x) at the point х₀.

Formulate properties of continuous functions at a point.

37. One-Sided Limits.

Find the one-side limits 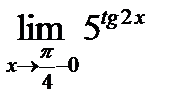and .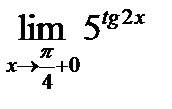

38. Discontinuity of the first kind.

Investigate for continuity function .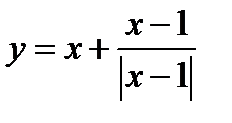

39. Discontinuity of the second kind.

Investigate for continuity function .

40. Derivatives of Functions.

The geometric Interpretation of the Derivative.

Prove that .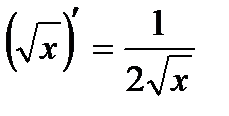

41. Differentiations Rules.

Find the derivative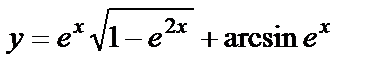

42. The Rolle Theorem.

The geometric Interpretation.

If 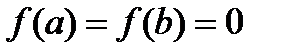, as it is possible to formulate Rolle's theorem?

43. The L'Hopital Rule.

Find the limit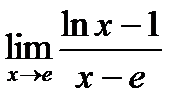

44. Increasing and Decreasing Functions.

Maxima and Minima of Functions.

Find extremes of the function .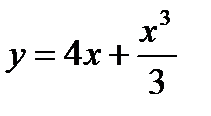

45. Curvature of Functions.

Find the inflection point and the intervals of convexity of the curve 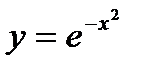(Gaussian curve).

46. Indefinite Integrals.

Its properties.

Evaluate the integral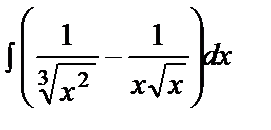

47. Integration by Substitution.

Evaluate the integral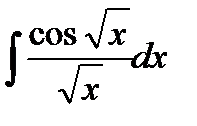

48. Integration by Parts.

Evaluate the integral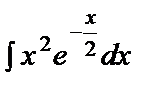

49. Integration of Rational Functions.

Evaluate the integral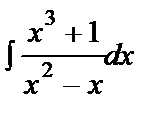

50. Integration of Trigonometric Functions.

Evaluate the integral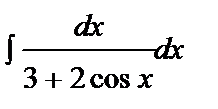

51. The definite Integral. Its properties.

Evaluate the integral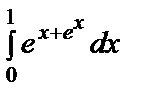

Date: 2015-04-20; view: 1628