List of questions to the exam

1. Basic information about the matrices.

Kinds of matrices.

Find the sum of matrices: .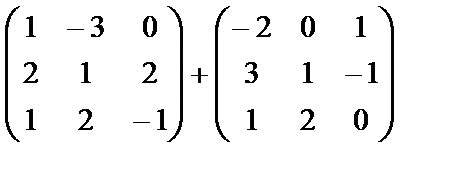

2. Operations on matrices.

Find the product of matrices: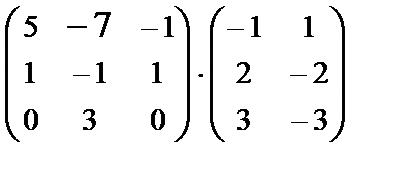

3. What is the determinant order two?

What is the determinant order three?

Their properties.

Calculate the determinant: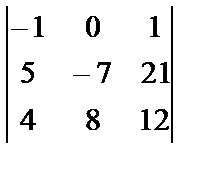

4. Given a square matrix order n. What is the minor of the element ?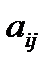

What is the cofactor (algebraic complement) of the element ?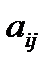

State the Laplace's theorem.

Calculate the determinant by Laplace's theorem: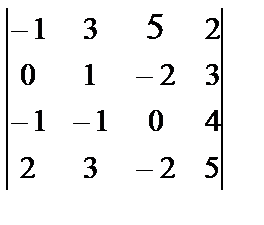

5. Let A is a square matrix order n. Give the definition of inverse matrix.

How to calculate the inverse matrix using a algebraic complement?

Find the inverse matrix: .

6. What actions are called elementary transformations in the matrix?

Describe the method elementary transformations to finding inverse matrices.

Find the inverse of a matrix by the elementary transformations method: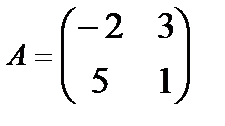

7. What is the rank of matrix.

Find rank of the matrix: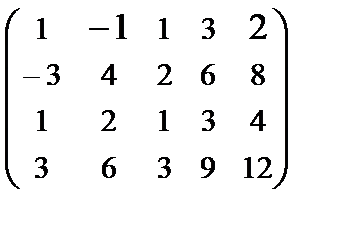

8. The system of m linear equations with n unknowns.

The basic concepts.

What is the matrix and the augmented matrix of system?

State the Kronecker–Capelli's theorem.

Investigate the system for consistency by the Kronecker–Capelli's theorem:

9. The system of n linear equations with n unknowns.

Cramer's rule.

Solve the system of equations by Cramer's rule: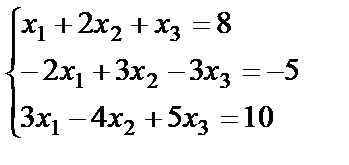

10. Solution of n linear equations with n unknowns by the inverse matrix method.

Solve the system of equations by method of inverse matrix:

11. The system of m linear equations with n unknowns.

The Gauss method.

Solve the system of equations by the Gauss method: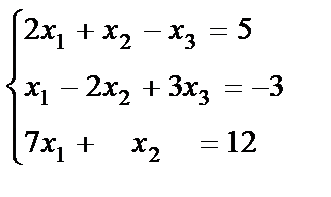

12. The system of linear homogeneous equations.

Solve the homogeneous system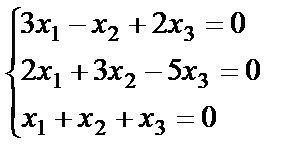

13. Let 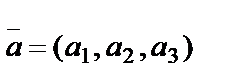and 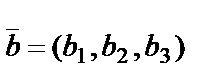are vectors in the space.

Find the length of the vector .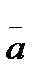

How to multiply the vector 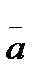by constant ?

Find the sum of vectors 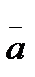and .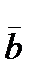

14. What is the scalar product of vectors 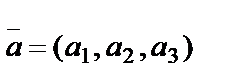and ?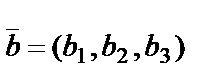

Given a vectors а=(1,-2,0) and b=(5,0,-1). Find the scalar product and angle between them.

15. What is the vector product of vectors 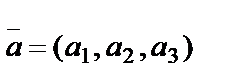and ?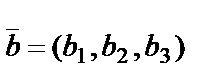

Find the vector product of vectors а=(1,-2,0) and b=(5,0,-1).

16. Linear dependence and independence of vectors.

Investigate, that the vectors x = (3,2, -1), y = (2, -1,3) and z = (1,3, -4) linearly dependent or no?

17. What kind of vectors constitute a basis?

Decomposition of the vector in the basis.

Prove that vectors 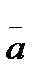, , 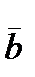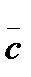is a basis. Expanded in the basis ( 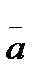, , 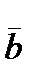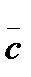) the vector 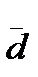: 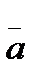=(2, -1, 5), 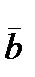=(3, 2, 1), 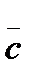=(1, 1, 0), =(5, 6, -3).

18. The distance between two points 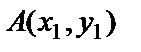and .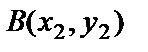

Division the segment AB in a given ratio 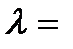АК:КВ.

Given a triangle with vertices О(0;0), А(8;0), В(0;6). Find the length of the median ОС and the bisector OD.

19. First-order line in the plane.

Given a triangle with vertices А(-2;0), В(2;6), С(4;2), and median ВЕ and height BD of the triangle are given. Write the equations of lines АС, ВЕ and BD.

20. Parallelism and perpendicularity of lines.

Write the equation of a line, parallel and perpendicular to the line 3х+5у=7, and passing through М(2,-4).

21. The distance from the point to the line.

Given a triangle with vertices А(-2;0), В(2;6), С(4;2). Find the distance from the length vertices А to the line BС.

22. The general equation of second-order curves.

What is the circle?

Find the coordinates of the center and the radius of the circle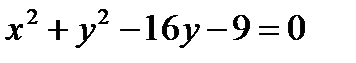

23. What is the ellipse?

The focus, the eccentricity, directrix of the ellipse.

Find he focus, the eccentricity, directrix of the ellipse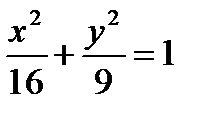

Date: 2015-04-20; view: 3786