
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Decoding of the nonsystematic convolutional codes
Nonsystematic convolutional codes are usually specified by polynomials in an octal notation, therefore for construction of the encoder it is necessary to convert polynomials in binary form.
Let's consider the elementary nonsystematic code (7, 5). For getting generator polynomials we will convert figures in binary and polynomial notations:
G(1) = 78 = 1112 ® D2 + D + 1,
G(2) = 58 = 1012 ® D2 + 1.
 |
The flow diagram of the encoder corresponding to polynomials G(1) and G(2), is resulted in fig. 1.8a. The state diagram for this encoder is shown in figure 1.8b.
Figure 1.8 – Flow (a) and state (b) diagrams of the encoder (7, 5)
Convolutional encoder as the final automatic machine with memory is described by the state diagram. Internal states of the encoder are the symbols containing in (K – 1) register cells (beginning from an encoder input). The encoder in fig. 1.8a can be in one of four states S1S2 = (00, 10, 11, 01), as K = 3. The diagram represents the directed graph which contains all states and describes possible transitions from one state to another, and also symbols of inputs/outputs of the encoder, accompanying these transitions. Encoder states are shown in circles; arrows show the possible transitions. Symbols above arrows show encoder inputs/outputs a/b(1)b(2), corresponding to each transition.
The development of the state diagram in time forms the trellis diagram (fig. 1.9). In the trellis the states are shown by the trellis points, transitions connect them by the lines. The trellis diagram represents all resolved paths on which the encoder can move ahead at coding.
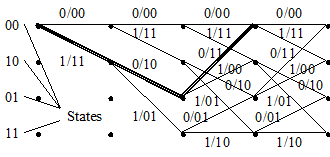 |
Figure 1.9 – Trellis diagram of the encoder (7, 5)
To determine free code distance of CvC (7, 5) we have to encode the single influence of kind ei = 1 0 0 0 0 0 0 . . . 0 by the formula (1.22):
v = 11 10 11 00 00 00 00…
W(v) = 5, so df = 5.
The way of the coding of such sequence is shown in the fig. 1.9 by double branches.
Constraint length of such code and the amount of informative bits in the limits of CL are
Na = n0 (K + 1) = 2 (2 + 1) = 6, Ka = K + 1 = 3.
As the amount of inputs of the encoder (7, 5) k0 = 1, and the amount of the outputs n0 = 2, relative information transfer rate and redundancy are
R = k0/n0 = 1/2, ρ = 1 – R = 1/2.
Nonsystematic codes can be decoded by probabilistic algorithms of decoding, i.e. the sequential decoding algorithm (SDA) and the Viterbi algorithm (VA).
The idea of the sequential decoding is the fallowing. Path must proceed only on the path tree which looks like most probable. A path is a certain sequence of combinations of the encoder output (on a transmission), corresponding to the certain informative sequence acting in the input of the encoder. Totality of such output sequences forms this tree, where every branch corresponds to the certain sequence in the output of the encoder.
Viterbi algorithm is modified variant of the sequential decoding algorithm, which differs from it on some positions:
- the search of optimal path is realized on a few paths (branches);
- the search of optimal path is realized on a trellis, which is got from the path tree by shorting of the similar (identical) states of knots and branches;
- the specific number of operations, necessary for decoding of code sequences corresponding to single bit, does not depend on the number of the received error symbols and is permanent.
Decoding on Viterbi algorithm is tracing on a trellis diagram of a path with maximum posterior probability. At decoding we choose such sequence of branches 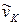 , which provides a sum minimum
, which provides a sum minimum
PM = 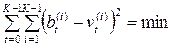 , (1.29)
, (1.29)
where 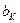 – input sequence of the decoder;
– input sequence of the decoder;  – set of code branches estimation.
– set of code branches estimation.
The expression (1.29) is the decoded path metrics (PM). The path metrics is the sum of branches metric: PM = 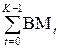 , where branches metrics are
, where branches metrics are 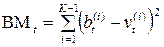 . In the discrete channel for an estimation of distances use Hamming metrics.
. In the discrete channel for an estimation of distances use Hamming metrics.
The periodic structure of the trellis diagram essentially simplifies comparison and a choice of paths according to rules (1.29). The amount of states on a trellis is limited, and two at random enough long paths have, as a rule, the common states. Sections of the paths entering these states are necessary to compare and choose a path with the least (minimum) metrics. Such path is called survived. According to Viterbi algorithm comparison and cutting of paths sections make periodically on each step of decoding. We will consider decoding (7, 5) which symbols are transferred on the discrete channel. In this case the branches metrics BM is equal to Hamming distance between a bit set b(1)b(2) in the decoder input and a bit set v(1)v(2), corresponding to the given branch in the trellis diagram. If b(1)b(2) = 01, possible values of BM for a code (7, 5) with a trellis represented in fig. 1.9, will be: BM(00) = 1, BM(01) = 0, BM(11) = 1 and BM(10) = 2. The path metrics is the sum of metrics of the branches forming some path on the trellis diagram. The state metrics SM are equal to PM which comes to an end in the given state.
In fig. 1.10 development of decoding process for code (7, 5) is shown. Pairs of symbols from the channel b(1)b(2) = 11 10 00 11 01... enter a decoder input. Figures above branches designate branches metrics; figures in circles designate state metrics. In the initial moment of time the decoder is in a state 00 and initial metrics
SM(00) = 0. If from the channel symbols 11 enter, metrics of two branches leaving this state, BM(00) = 2 and BM(11) = 0. Metrics of the states 00 and 11 are equal to metrics of entering branches: SM(00) = 2 and SM(10) = 0. The following step is similar, when symbols 10 enter from the channel. Here BM(00) = 1, BM(11) = 1 and BM(10) = 0, BM(01) = 2. State metrics on this step are defined now as the sums of metrics of entering branches with metrics of the previous states: SM(00) = 2 + 1 = 3,
SM(10) = 2 + 1 = 3, SM(01) = 0 + 0 = 0, SM(11) = 0 + 2 = 2. On this step the development of the trellis diagram comes to end.
Two paths lead to each new state. For example, to the state 00 leads paths from the states 00 and 01. The decoder calculates paths metrics as the sums of metrics of the previous states and metrics of entering branches.
Then goes paired comparison of metrics of the paths entering into each state. As a result of comparison the decoder chooses the smaller metrics and it consider as
Figure 1.10 – Decoding process for code (7, 5)
 |
the metrics of the given state for the subsequent step of decoding. The path entering into the given state with the smaller metrics is survived. The paths entering states with the big metrics, consider rejected. They are shown on the trellis diagram by shaped lines.
If metrics of compared paths are identical, a choice one of two paths make in a random path. On each step as a result of comparison half of possible paths is rejected and further is not used. Other half forms continuations of paths for a following step of decoding. There are two variants of paths continuation from each state on a following step again. It provides a constancy of the calculations made on each step. The decoder traces a path having the minimum distance from a path which generates the encoder on a trellis.
The resulted path with minimal PM = 1 is shown in fig. 1.10 by bold line, the output of the decoder is 1 0 1 1 0.
Decoding of convolutional code can be realized with hard or soft decisions, and in the output decoder we will get hard or soft data. At decoding with a hard decision, every received bit is “0” or “1” depending on that less or more these bits than threshold value. Redundant information, added in the encoder, is used in a decoder for determination of errors and, on possibility, their correction. Output data of decoder is the corrected code word.
Date: 2015-02-16; view: 1408
| <== previous page | | | next page ==> |
| Convolutional codes | | | Soft output Viterbi algorithm |