
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Convolutional codes
1.3.1 Basic parameters of convolutional codes
Currently convolutional codes (CvC) find large practical application in telecommunications. It above all things concerns to data transmission systems, digital broadcast, television and mobile networks GSM. The convolutional encoding got further development with appearance of the Viterbi algorithm.
A basic task at encoding by CvC, as well as CC, consists in forming of check sequence and time-division multiplexing of it with informative sequence. Using operator of delay D on a time τ0 (an operator Dv corresponds to the delay on vτ0), informative A(D) and check B(D) sequences can be presented as binary polynomials with the half-infinite number of elements:

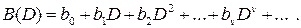
Every check bit bv at the convolutional encoding is linear combination of information bits A(D) taking into account some fixed polynomial G(D), degree of which is more than zero, i.e.
B(i)(D) = G(i)(D) 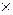 A(D), (1.22)
A(D), (1.22)
where G(i)(D) – generator polynomials that determines corrective ability of CvC.
The binary convolutional encoder contains the shift register on K cells and adders modulo 2 on the for code symbols formation. Inputs of adders are defined by register cells. Links of i-th adder with cells of j-th register are described by a generator polynomial (for codes with a speed R = 1/n0)
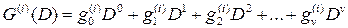 ,
,
where  = 1, if link of i-th adder with s-th cell exists,
= 1, if link of i-th adder with s-th cell exists,
 = 0, if such link is not present.
= 0, if such link is not present.
Thus, the convolutional encoder is described by a set of factors
 = {
= { 
 …
…  }.
}.
The parameters of CvC are:
1. Free code distance. Unlike block codes for systematic CvC free code distance df is determined by weight (amount of ones) of impulsive description of the encoder Wt(v). Impulsive description of encoder v is a response on the single influence of kind ei = 1 0 0 0 0 0 0 . . . 0.
2. Constraint length (CL). A encoder of any CvC is a device with memory, containing of K memory cells, in inputs of which every clock cycle enters k0 input bits, and in an output appears n0 bits. Parameter
Na = n0 (K + 1) (1.23)
determines constraint length, which plays the same role as the length of the code combination of the block code.
For compactness of the denotation of the systematic convolutional codes the record of the kind (Na, Ka), where Ka = K + 1 is the amount of informative bits in the limits of CL.
3. Correcting capability in the limits of CL of a convolutional code is a number of errors that can be corrected by the code. It can be calculated by the formula (1.6):
tc = [(df – 1)/2], (1.24)
where [x] is the largest integer, but not more than x.
4. Relative information transfer rate and redundancy of the CvC are determined as follows:
R = k0/n0, (1.25)
ρ = 1 – R. (1.26)
1.3.2 Decoding of the systematic convolutional codes
The sufficient condition of systematic CvC with threshold decoding construction with R = 1/2 is implementation of two positions:
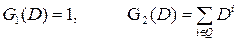 , (1.27)
, (1.27)
where 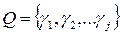 is perfect difference set.
is perfect difference set.
Subset consisting of j integers is difference set (DS) with parameters (v, j, λ), if all differences on the modulo v at i ≠ k will be equal to 1, 2, 3, ..., v – 1 exactly λ times. Difference sets with λ = 1 are perfect, or simple. Binary signals built on the basis of perfect DS have two-digit autocorrelation function and find application not only in a theory and technique of the noiseproof encoding but also in the different systems of telemetry and radio-locations.
Perfect DS, i.e. with parameters (v, j, 1) have property "no more than one coincidence". It means that at any time shift of impulsive sequence, consistent with the elements of DS, will be no more than one coincidence of impulses of initial and moved sequence. This property allows realize the threshold decoding of systematic convolutional codes.
For example, the set Q = {0, 2, 5, 6} is perfect difference set with parameters j = 4, v = 13. The choice of these four numbers can be explained by the fact that all possible differences on the modulo v form sequence of positive natural numbers N = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. This can be explained as follows. Completing all possible difference subtractions of Q, given that 13 ≡ 0 mod 13, we obtain:
0 – 0 = 0,
0 – 2 º 13 – 2 = 11, 2 – 0 = 2,
0 – 5 º 13 – 5 = 8, 5 – 0 = 5,
0 – 6 º 13 – 6 = 7, 6 – 0 = 6,
2 – 5 º 2 + 13 – 5 = 10, 5 – 2 = 3,
2 – 6 º 2 + 13 – 6 = 9, 6 – 2 = 4,
5 – 6 º 5 + 13 – 6 = 12, 6 – 5 = 1.
Perfect DS Q = {0, 2, 5, 6} determines systematic CvC with generator polynomials
G1(D) = 1, G2(D) = 1 + D2 + D5 + D6. (1.28)
Here the first polynomial corresponds with the generation of information symbols ai, and the second with the formation of check symbols bi.
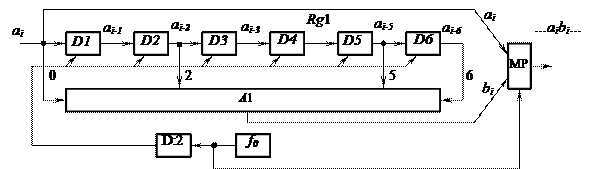 |
The flow diagram of this encoder is shown in the fig. 1.5. The shift register Rg1, consists of six memory cells D1, ..., D6, which save received binary symbols. Multi-input adder modulo 2 A1 intends for the generation of check symbols. The multiplexer MP realizes time multiplexing of information symbols ai, ai–1, ai–2, …, ai–n and check bits bi, bi–1, bi–2, …, bi–n, where i is the number of symbol in the input of Rg1. The frequency of reference generator f0 must be selected according to
Figure 1.5 – Flow diagram of the encoder CvC with polynomials
G1(D) = 1, G2(D) = 1 + D2 + D5 + D6.
transmission rate of the communication channel. Divisor D:2 with factor of division 2 determines the frequency of timed pulses of the encoder.
To generate the check symbols bi inputs of A1 connect to the outputs of the register Rg1 as follows
bi = ai Å ai–2 Å ai–5 Å ai–6 .
To determine free code distance of CvC, which is shown in the fig. 1.5, we have to encode the single influence of kind ei = 1 0 0 0 0 0 0 . . . 0 by the formula (1.22):
v = 11 00 01 00 00 01 01 00 00 …
W(v) = 5, so df = 5.
Constraint length of such code and the amount of informative bits in the limits of CL are
Na = n0 (K + 1) = 2 (6 + 1) = 14, Ka = K + 1 = 7.
So, this code can be denoted as (14, 7).
As the amount of inputs of the encoder (14, 7) k0 = 1, and the amount of the outputs n0 = 2, relative information transfer rate and redundancy are
R = k0/n0 = 1/2, ρ = 1 – R = 1/2.
Flow diagram of the convolutional decoder with threshold decoding method is shown in fig. 1.6. The algorithm of threshold decoding method is the following. After digital demultiplexing in DMP of the information and check bits of the received sequence with noise symbols ei
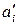 = ai Å ei and
= ai Å ei and 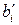 = bi Å ei ,
= bi Å ei ,
 |
informative
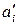 enter register Rg2. As a result, at forming of check symbols of the encoder bi, the sequence of local check symbols appears in a decoder
enter register Rg2. As a result, at forming of check symbols of the encoder bi, the sequence of local check symbols appears in a decoder
 =
= 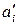 Å
Å  Å
Å  Å
Å 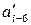 .
.
Figure 1.6 – Flow diagram of the convolutional decoder (14, 7)
After adding the check symbols, formed in the decoder  and received from the channel
and received from the channel 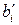 , in the output of A2 the syndrome sequence Si appears, that
, in the output of A2 the syndrome sequence Si appears, that
enters the register Rg3. Note that ones in this sequence will appear only in the case of mismatch of  and
and 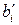 . Connecting of this register to the threshold device TD corresponds to the reverse order of connections in Rg2. One in the output of threshold device is formed for the correction of error bit, which is in the output of Rg2, only at the presence in its inputs of three in any order or four ones.
. Connecting of this register to the threshold device TD corresponds to the reverse order of connections in Rg2. One in the output of threshold device is formed for the correction of error bit, which is in the output of Rg2, only at the presence in its inputs of three in any order or four ones.
As a result of analysis of Si by TD, a decoder makes decision about possible validity of the received informative sequence 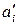 . If for some time error in a channel does not appear, then in a syndrome register Rg3 will follow only zero symbols, because
. If for some time error in a channel does not appear, then in a syndrome register Rg3 will follow only zero symbols, because 
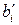 = 0. At the presence of errors in the output of decoder in the sequence Si, except zeros, ones appear.
= 0. At the presence of errors in the output of decoder in the sequence Si, except zeros, ones appear.
A threshold device (fig. 1.7) with connecting to the syndrome register, determines character of the following ones and zeros. If necessary, TD gives out the signal of error correction in the second input of adder A3 (i.e. one) that synchronizes with the moment of read-out of the error information bit from the output of Rg2.
 |
Figure 1.7 – Flow diagram of threshold device
In the given flow diagram of decoder (see a fig. 1.6) there is a feed-back with memory cells of Rg2 for the correction of Rg3. It is made to prepare favourable conditions at the correction of the next error information bits. Note that at intensive interferences in a communication channel the feed-back of decoder can give a result in additional formation of errors.
Date: 2015-02-16; view: 1515
| <== previous page | | | next page ==> |
| Meggitt decoder of cyclic codes | | | Decoding of the nonsystematic convolutional codes |