
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Syndrome decoding of cyclic codes
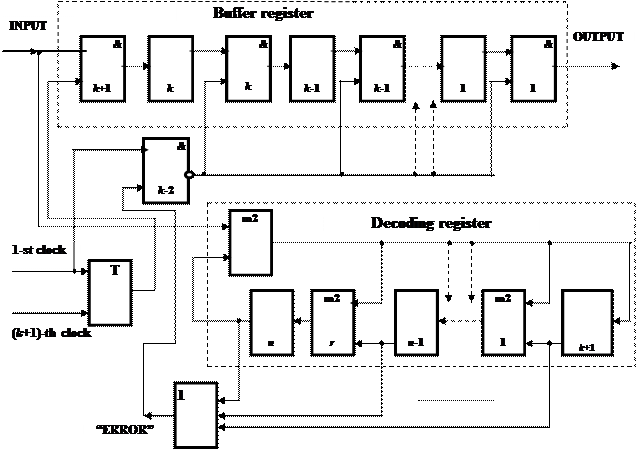
Let’s consider the decoders of cyclic codes. The construction of decoder for errors detection is shown in a fig. 1.3.
The decoder has: buffer register of k-bits; decoding register, the chart of which is similar to the chart of the encoder; logical charts OR, AND with the trigger, executing functions of the keys.
A decoder works as follows. The received informative sequence writes simultaneously in buffer and in decoding registers. On (k+1)-th clock cycle the electronic key &k+1 is closed and in this case the information bits of the received code combination appear in a buffer register only. Check bits continue to enter decoding register.
On (n+1)-th clock cycle, after the reception of the last digit of code combination, the electronic key &k+2 opens. If code combination is accepted without errors, then in the cells of decoding register only zeros will be written, and the signal "ERROR" will be absent. A presence even in one cell of decoding register of one testifies to the errors in the received information. In the output of the chart “OR” at this case a signal "ERROR" will appear, that can be used for deleting of the received code combination with errors accumulated in the buffer register.
If a decoder is used in the mode of the correction of errors, then it is necessary to specify the place of the error information bits. In the structure of the decoder instead of chart “OR” use the decipherer of the syndrome, producing in its output signal “1” during fixing in the cells of decoding register of remainder different from zero.
Figure 1.3 – Flow diagram of the cyclic (n, k) code decoder
 |
When ones appear in an output of the adder modulo 2, they coincided with passing of the error informative bit. Thus error bit, getting through output adder, changes its sign on inverse, i.e. correct.
For the position-fix of an error element received code combination of cyclic code use a remainder from dividing of this code combination by the generator polynomial Ð(õ). The got remainder R(x) is the syndrome of error. This procedure will be realized by comparison of remainder R(x) with the table of syndrome combinations formed by dividing of errors vectors e(x) by the generator polynomial Ð(õ).
As an example let’s consider the cyclic code decoder (15, 11) with the generator polynomial Ð(õ) = õ4 + õ + 1, correcting single errors. For this code a single error vector e(x) = õ14 (100000000000000) is divided by the generator polynomial Ð(õ) = õ4 + õ + 1, forming the remainder S14(x) = õ3 + 1. If in the accepted combination of cyclic code the error is in 15th position, i.e. bit õ14, then a remainder from dividing of it by Ð(õ) will coincide with S14(x).
Syndrome combinations for the errors vectors õ13, õ12, õ11, õ10, õ9, õ8, õ7, õ6, õ5, õ4, õ3, õ2, õ1, õ0 form similarly. For the chosen cyclic code with n = 9 have syndromes in table 1.2.
Comparing the remainder R(x) with syndrome combinations Si(x), 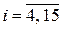 , get information about an error element in the accepted combination of the cyclic code.
, get information about an error element in the accepted combination of the cyclic code.
Table 1.2 – The syndrome table for cyclic (15,11) code
| Error | Syndrome | Error | Syndrome |
| õ14 | õ3 + 1 | õ6 | õ3 + õ2 |
| õ13 | õ3 + õ2 + 1 | õ5 | õ2 + õ |
| õ12 | õ3 + õ2 + õ + 1 | õ4 | x + 1 |
| õ11 | õ3 + õ2+ õ | õ3 | õ3 |
| õ10 | õ2 + õ + 1 | õ2 | õ2 |
| õ9 | õ3 + õ | õ1 | õ1 |
| õ8 | õ2 + 1 | õ0 | |
| õ7 | õ3 + õ + 1 |
So, the correction of errors is based on correspondence between the amount of syndromes values and the amount of the corrected errors. However at multiplicity of errors t > 1 this accordance breaks. As a rule, takes place additional input of error symbols, that is the serious defect of the syndrome decoder.
Date: 2015-02-16; view: 1975
| <== previous page | | | next page ==> |
| The relative information transfer rate of cyclic codes | | | Meggitt decoder of cyclic codes |