
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Cyclic codes
1.2.1 Basic construction principles of cyclic codes
Cyclic codes were originally created to simplify the encoding and decoding schemes. Subsequently their high corrective properties was detected, thus providing its wide application in practice and, in particular, the wide application in modern telecommunication technologies.
In the construction of CC, code combinations are taken to represent in the polynomial form:
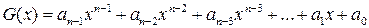 , (1.1)
, (1.1)
where  coefficients, specifying values 0 or 1.
coefficients, specifying values 0 or 1.
For example, the code combination 1100101 can be written as

The main property of CC is the follow: the cyclic shift of single elements of the permitted combination also results to the permitted code combination. Thus, if the combination 1000111 is permitted combination, then combinations 0001111, 0011110, ... are permitted.
Cyclic codes are determined with the generator polynomials P(x) of degree r. The generator matrix of CC can be formed from the generator polynomial by a cyclic shift of the last:
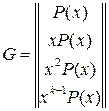 (1.2)
(1.2)
Directly from the generator matrix implies that all permitted combinations of a cyclic code can be divided into generator polynomial without remainder. Because of this fact, it is a very easy to determine if the received code combination is permitted or not.
In order to have necessary characteristics of the polynomials that representing code combinations of cyclic code, implementation of terms that represent properties of the generator polynomial Π(υ) is needed:
- generator polynomial P(x) must be irreducible (in this case the generator polynomial divides without remainder only to itself);
- binomial of type 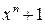 must be divisible by a generator polynomial P(x) without remainder (that is the normal operation of division).
must be divisible by a generator polynomial P(x) without remainder (that is the normal operation of division).
Lets consider the process of forming code combination of CC. Each codeword G(x) multiplied by 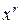 , then divided by generator polynomial of degree r (the amount of check bits). As a result of multiplying the degree of each member, included in the polynomial G(x), increases by r. In the division of product
, then divided by generator polynomial of degree r (the amount of check bits). As a result of multiplying the degree of each member, included in the polynomial G(x), increases by r. In the division of product 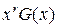 by P(x) we take quotient Q(x) the same degree as G(x). In addition, if the product
by P(x) we take quotient Q(x) the same degree as G(x). In addition, if the product 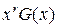 is not divided by P(x), then you have the remainder R(x):
is not divided by P(x), then you have the remainder R(x):
 (1.3)
(1.3)
where the sign 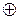 denotes XOR (addition modulo 2).
denotes XOR (addition modulo 2).
As quotient Q(x) has the same degree as G(x), then it is also a combination of simple k-elements code. Multiplying both sides of the equality (1.3) by P(x), we have
 (1.4)
(1.4)
Thus, the codeword of a cyclic code can be obtained in two ways:
1. Multiplying the k-element combinations of simple code by generator polynomial P(x);
2. Multiplying the k-element codeword of simple code by the monomial 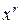 and adding R(x).
and adding R(x).
The first method leads to the formation of inseparable (nonsystematic) cyclic code. Inseparability greatly complicates the decoding process, so in practice, the second method of constructing codeword of cyclic code is used.
Code combinations should be different from each other by interchange and the presence of ones and zeros. Code distance (Hamming distance) makes possible to distinguish two code combinations from each other. The code distance between the combinations determined by the number of units obtained after addition modulo 2. For redundant codes, including cyclic, the code distance between the code combinations should always be not less than the minimum code distance.
The parameters of CC include:
n the length of the code combination;
k the length of information part of the code combination;
r the length of the check part of the code combination;
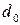 minimum code distance;
minimum code distance;
P(x) generator polynomial of a cyclic code.
Minimum code distance is associated with the amount of detecting and correcting errors as follows:
 (1.5)
(1.5)
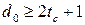 , (1.6)
, (1.6)
where  the amount of detected errors;
the amount of detected errors;
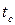 the amount of correcting errors;
the amount of correcting errors;
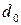 minimum code distance.
minimum code distance.
To correct all errors of multiplicity up  and simultaneous detection of all errors of multiplicity no more
and simultaneous detection of all errors of multiplicity no more  code distance must satisfy the condition
code distance must satisfy the condition

Minimum code distance is only partially describes the corrective properties of redundant code, then they allow to detect and correct errors of higher multiplicity than provided in the calculation of the code parameters. The number of permitted code combinations is determined by the number of data bits and is equal
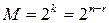 .
.
Thus, the number of permitted combinations in  times less than the total number of combinations.
times less than the total number of combinations.
Redundancy of the code is the relation ρ = r/n. The question of the minimum necessary redundancy of the code for the given minimum code distance and length of the code is still pending. There are only upper and lower edges (limits) of check bits amount, which are listed below:
Hamming edge 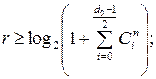 (1.7)
(1.7)
Upper Plotkin edge 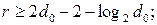 (1.8)
(1.8)
Elias edge 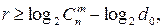 where
where 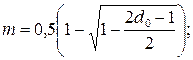 (1.9)
(1.9)
Lower Varshamov-Gilbert edge 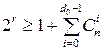 , or
, or 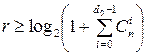 . (1.10)
. (1.10)
The most optimal approach provides a criterion Varshamov-Gilbert edge.
Knowing the length of information part of a cyclic code, selecting the amount of check bits by the formula (1.10), we can easily calculate the main parameters of a cyclic code: n, k, r, as n = k + r. In a special table (see Table 1.1) for calculated parameters we can choose a polynomial P(x) and eventually build a codec of the cyclic code.
Table 1.1 Generator polynomial of cyclic codes
| Degree of P(x) | Kind of polynomial | |||
| x+1 | ||||
| x2+x+1 | ||||
| x3+x+1 | x3+x2+1 | |||
| x4+x+1 | x4+x3+1 | x4+x3+x2+x+1 | ||
| x5+x3+1 | x5+x4+x2+x+1 | x5+x4+x3+x2+1 | ||
| x7+x3+1 | x7+x4+x3+1 | x7+x3+x2+x+1 | ||
| x8+x4+x3+x+1 | x8+x5+x4+x3+1 | x8+x7+x5+x+1 | ||
| x9+x4+x2+x+1 | x9+x5+x3+x2+1 | x9+x6+x3+x+1 | ||
| x10+x3+1 | x10+x4+x3+x+1 | x10+x8+x3+x2+1 | ||
| x11+x2+1 | x11+x7+x3+x2+1 | x11+x8+x5+x2+1 | ||
| x12+x6+x4+x+1 | x12+x9+x3+x2+1 | x12+x11+x6+x4+x2+x+1 | ||
| x13+x4+x3+1 | x13+x10+x9+x+1 | x13+x12+x11+x2+1 | ||
| x14+x13+x11+x9+1 | x14+x12+x10+x4+x2+x+1 | x14+x12+x2+x+1 | ||
| x15+x12+x3+x+1 | x15+x13+x5+x+1 | x15+x14+x13+x10+x2+x+1 | ||
| x16+x15+x7+x2+1 | x16+x14+x12+x3+x2+x+1 | x16+x12+x5+x+1 | ||
Date: 2015-02-16; view: 1423
| <== previous page | | | next page ==> |
| ERROR-CORRECTING CODES | | | The relative information transfer rate of cyclic codes |