
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
C. The Physics Behind Cruise Control Systems
Early cruise control systems lacked the fancy computer programming that modern systems utilize. As a result, early systems were not as good at actually keeping the speed of the car constant; the throttle was held in position, but as other forces on the vehicle varied, the vehicle speed fluctuated some. The logic of modern control systems in cruise control comes out of the need to compensate for the physical forces that act on a car and try to change its speed.
In a simplified ideal situation, only two forces would be present in the movement of a car—the friction between the wheels and the road, and the force with which the engine pulls the car. In such a situation, the control system would be very simple. A simple proportional controller could control the speed by simply having set throttle positions for each possible speed setting. However, this idealized situation is far from reality. Cars have varying drag forces due to wind, varying mechanical component friction due to speed and temperature, varying gravitational forces due to inclines, and varying engine force due to hydraulically activated steering pumps.
For the sake of understanding the basics of how the controls work, the simplest case mentioned is a good starting point. Only forces are the engine force and the wheel friction are considered, so the main goal of a cruise control system will be to get the car to the desired speed, like what happens does when a driver hits the resume button. Once this resume speed is achieved, the forces on the car will not be changing, so no logic will be needed for maintaining the speed. The logic instead will deal with making the car accelerate up to the desired speed rapidly without overshooting that desired speed by very much. Calling the mass of the car m, the velocity v, the force from the engine F, and the friction coefficient f, the model for the car becomes:
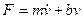 (1)
(1)
The goal is to create a simple transfer function from this equation that can be used in an open loop system. This transfer function will be the ratio of the velocity over the engine force. Performing a Laplace transform to the physical equation makes this possible:
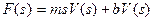 (2)
(2)
The transfer function then becomes:
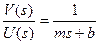 (3)
(3)
Since we actually want to track the velocity of the car, this can also be looked at the following way:
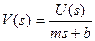 (4)
(4)
Date: 2014-12-22; view: 3430
| <== previous page | | | next page ==> |
| B. System Components | | | D. Simple Block Diagram Simulations |