Assembler language Basic concepts

Contents

2.2.1 Information in the computers

2.2.2 Data representation methods

2.2.1 Information in the computer

Contents

2.2.1.1 Information units

2.2.1.2 Numeric systems

2.2.1.3 Converting binary numbers to decimal

2.2.1.4 Converting decimal numbers to binary

2.2.1.5 Hexadecimal system

2.2.1.1 Information Units

In order for the PC to process information, it is necessary that this information be in special cells called registers. The registers are groups of 8 or 16 flip-flops.

A flip-flop is a device capable of storing two levels of voltage, a low one, regularly 0.5 volts, and another one, commonly of 5 volts. The low level of energy in the flip-flop is interpreted as off or 0, and the high level as on or 1. These states are usually known as bits, which are the smallest information unit in a computer.

A group of 16 bits is known as word; a word can be divided in groups of 8 bits called bytes, and the groups of 4 bits are called nibbles.

2.2.1.2 Numeric systems

The numeric system we use daily is the decimal system, but this system is not convenient for machines since the information is handled codified in the shape of on or off bits; this way of codifying takes us to the necessity of knowing the positional calculation which will allow us to express a number in any base where we need it.

It is possible to represent a determined number in any base through the following formula:

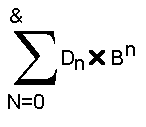
Where n is the position of the digit beginning from right to left and numbering from zero. D is the digit on which we operate and B is the used numeric base.

2.2.1.3 converting binary numbers to decimals

When working with assembly language we come on the necessity of converting numbers from the binary system, which is used by computers, to the decimal

system used by people.

The binary system is based on only two conditions or states, be it on(1) or off(0), thus its base is two.

For the conversion we can use the positional value formula:

For example, if we have the binary number of 10011, we take each digit from right to left and multiply it by the base, elevated to the new position they are:

Binary: 1 1 0 0 1

Decimal: 1*2^0 + 1*2^1 + 0*2^2 + 0*2^3 + 1*2^4

= 1 + 2 + 0 + 0 + 16 = 19 decimal.

The ^ character is used in computation as an exponent symbol and the * character is used to represent multiplication.

2.2.1.4 Converting decimal numbers to binary

There are several methods to convert decimal numbers to binary; only one

will be analyzed here. Naturally a conversion with a scientific calculator is much easier, but one cannot always count with one, so it is convenient to at least know one formula to do it.

The method that will be explained uses the successive division of two, keeping the residue as a binary digit and the result as the next number to divide.

Let us take for example the decimal number of 43.

43/2=21 and its residue is 1

21/2=10 and its residue is 1

10/2=5 and its residue is 0

5/2=2 and its residue is 1

2/2=1 and its residue is 0

1/2=0 and its residue is 1

Building the number from the bottom , we get that the binary result is

2.2.1.5 Hexadecimal system

On the hexadecimal base we have 16 digits which go from 0 to 9 and from the letter A to the F, these letters represent the numbers from 10 to 15. Thus we count 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E, and F.

The conversion between binary and hexadecimal numbers is easy. The first thing done to do a conversion of a binary number to a hexadecimal is to divide it in groups of 4 bits, beginning from the right to the left. In case the last group, the one most to the left, is under 4 bits, the missing places are filled with zeros.

Taking as an example the binary number of 101011, we divide it in 4 bits groups and we are left with:

10;1011

Filling the last group with zeros (the one from the left):

0010;1011

Afterwards we take each group as an independent number and we consider its

decimal value:

0010=2;1011=11

But since we cannot represent this hexadecimal number as 211 because it would be an error, we have to substitute all the values greater than 9 by their respective representation in hexadecimal, with which we obtain:

2BH, where the H represents the hexadecimal base.

In order to convert a hexadecimal number to binary it is only necessary to invert the steps: the first hexadecimal digit is taken and converted to binary, and then the second, and so on.

2.2.2 Data representation methods in a computer.

Contents

2.2.2.1.ASCII code

2.2.2.2 BCD method

2.2.2.3 Floating point representation

2.2.2.1 ASCII code

ASCII is an acronym of American Standard Code for Information Interchange. This code assigns the letters of the alphabet, decimal digits from 0 to 9 and some additional symbols a binary number of 7 bits, putting the 8th bit in its off state or 0. This way each letter, digit or special character occupies one byte in the computer memory.

We can observe that this method of data representation is very inefficient on the numeric aspect, since in binary format one byte is not enough to represent numbers from 0 to 255, but on the other hand with the ASCII code one byte may represent only one digit. Due to this inefficiency, the ASCII code is mainly used in the memory to represent text.

2.2.2.2 BCD Method

BCD is an acronym of Binary Coded Decimal. In this notation groups of 4 bits are used to represent each decimal digit from 0 to 9. With this method we can represent two digits per byte of information.

Even when this method is much more practical for number representation in the memory compared to the ASCII code, it still less practical than the binary since with the BCD method we can only represent digits from 0 to 99. On the other hand in binary format we can represent all digits from 0 to 255.

This format is mainly used to represent very large numbers in mercantile applications since it facilitates operations avoiding mistakes.

2.2.2.3 Floating point representation

This representation is based on scientific notation, this is, to represent a number in two parts: its base and its exponent.

As an example, the number 1234000, can be represented as 1.123*10^6, in this last notation the exponent indicates to us the number of spaces that the decimal point must be moved to the right to obtain the original result.

In case the exponent was negative, it would be indicating to us the number of spaces that the decimal point must be moved to the left to obtain the original result.

Date: 2014-12-22; view: 809