
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Chapter 3. Knapsack Systems 2 page
It is customary to choose the number n of components as the size and to give bounds for the components in terms of n. It is to be emphasized that all such bounds for the components are artificial from a mathematical point of view and restrict the generality of the problem because only a very small number of
instances fall within the bounds. This is apparent also in view of the general theory of Section 3.3.
In [Sh2], the bounds are given as follows. A proportionality constant d > 1 is fixed. Then the modulus m consists of dn bits. The component at, 1 < i < n, of the super-increasing vector A consists of dn — 1 — n + i bits. If d is not an integer, dn is replaced by- [<fn]. The leading bit is 1 in every number. This guarantees that A is always super-increasing and that one can choose m to exceed the sum of the components of A. In the original paper, [MeH], the choices n = 100 and d = 2 were recommended. This means that m consists of 200 bits and the components a100 grow in size from 100 to 199 bits.
In constructing the algorithm the initial observation is that it is not necessary to find the inverse multiplier u and modulus m actually used by the designer of the cryptosystem. Any pair (u, m) will do, provided u and m satisfy the conditions of modular multiplication as regards B, the result A of such a modular multiplication is super-increasing and m exceeds the sum of the components of A. (This implies that B results from A by strong modular multiplication with respect to m and u"1 = f.) Such pairs («, m) are referred to as trapdoor pairs. Once we have found a trapdoor pair, Lemma 3.1 becomes available, and we may decrypt using the resulting super-increasing vector. This is quite independent of whether or not our trapdoor pair and the resulting super-increasing vector are the ones actually used by the cryptosystem designer. On the other hand, the existence of at least one trapdoor pair is guaranteed by the fact that cryptosystem designer made use of such a pair. (Using the terminology of Section 3.3, we know a priori that the given knapsack vector B is super-reachable.)
| Recall that (b1u, mod m) = au where u is not a variable but the actual inverse multiplier we are looking for. Since a, is the first component in a super-increasing vector and m exceeds the sum of all components, a, must be very small in |
To find a trapdoor pair (u, m), we first consider the graphs of the functions bt u (mod m) for all values i = 1,..., n. The graph of bt u (mod m) consists of straight line segments, where the values u = pm/bf, p = 1,2,. .., are discontinuation points of the function. Thus, the graph of the function btu (mod m) has the sawtooth form of Fig. 3.1. This sawtooth curve is considered for each i = 1,. . ., n.
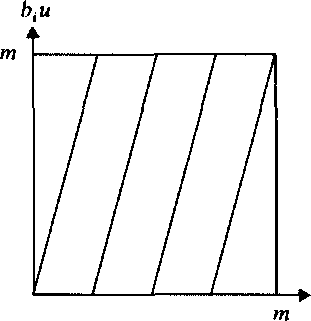 Fig. 3.1
Fig. 3.1
|
comparison with m. This implies that the trapdoor pair value of u must be close to some minimum of the fcj-graph. An explicit estimate concerning how close it must be presupposes some conventions (such as those indicated above) about the sizes of a, and m, as well as about the expected value of bUsually bi/ai is very large for small values of i. However, the cryptosystem designer may take care of that bijai < 1 for some values of i. Then some distances will be much larger than expected, which causes serious difficulties for the cryptanalyst.
Similarly we see that the trapdoor pair value of u must be close to some minimum of the fc2-graph. This implies (by the triangular inequality) that the two minima of the fa,- and b2-graphs must be close to one another.
One can proceed in the same way and consider more sawtooth curves. The fact that the trapdoor pair value of u is close to a minimum on each curve implies that all these minima are close to one another. Thus, instead of trying to find u itself, we may try to find "accumulation points" of the minima of our sawtooth curves. This amounts to constructing a small interval containing a minimum of each sawtooth curve. From this interval we also find a trapdoor pair value of u. By heuristic calculations (see [Sh2]) one can show that, for the value d = 2 of the proportionality constant, it suffices to analyze only four sawtooth curves to get a manageable (not too big) set of accumulation points for their minima. Any accumulation point of minima of all curves is among the accumulation points constructed for the minima of the four curves mentioned.
We now come to the problem of how to express these ideas in terms of inequalities. The first obstacle is that we do not know any value of a modulus m appearing in a trapdoor pair. This obstacle is easily overcome. We reduce the size of the picture so that m becomes 1. In other words, the lengths are divided by m. This operation does not affect the location of the accumulation points in which we are interested. For instance, if there was a t>rminimum near the seventh b3- minimum before the size reduction, the same certainly holds true after the size reduction.
The algorithm for finding a trapdoor pair consists of two parts. In the first part, we find candidates for an integer p such that the pth minimum of the b j -curve is an accumulation point we are looking for. The second part of the algorithm tests the candidates one by one. One of the tests has to succeed because the trapdoor pair value of u used by the cryptosystem designer determines one accumulation point.
A specific precaution has to be taken. The first part of the algorithm might produce too many (in comparison with the size of the problem) candidates for p. Therefore, we fix in advance a parameter r indicating the maximum number of candidates allowed. If the first part of the algorithm produces r + 1 candidates for p, the algorithm terminates and reports failure. The algorithm is stochastic with a negligible probability of failure.
On the other hand, we do not have to consider all components b2,. . ., b„ in the first part of the algorithm, but may fix in advance the value of another parameter s < n and consider only the components b2, ■ ■., bs. In other words, the first part of the algorithm produces numbers p such that the pth minimum of the b j -curve is nearby some minimum of the i>rcurve, for i = 2, . . . , s. Thus the values i > s are not considered at all in the first part of the algorithm, and it is very likely that entirely wrong values of p are produced. However, the second part of the algorithm checks through all values of i, 2 < i < n. A candidate p is rejected if, for some /, there is no minimum of the ft,-curve near the pth minimum of the 6j-curve. We already pointed out that s = 4 is in many cases a reasonable choice.
Consider the first part of the algorithm in more detail. The u-coordinate of the pth minimum of the b1 -curve is p/bl. (Recall that we reduced the picture in such a way that the modulus equals 1.) Hence, the condition that some minimum of the ft2-curve lies near the pth minimum of the ft,-curve can be expressed as
— e<Y--~-<e, 1 < p < i>! — 1, l<q<b2-l.
>> 1 b2
Multiplying by the product blb2 we obtain
- <5 < b2p — btq < 5, 1 < p < b1 - 1, 1 < q < b2 - 1 .
We write s — 1 inequalities of this latter form, one for each of the components b2,. . ., bs. How small the number S has to be chosen will be commented upon later. The first part of the algorithm finally outputs all integers p for which there are integers q, . . . such that all of the s — 1 inequalities are satisfied.
We now describe the second part of the algorithm. It tests numbers p produced by the first part until it is successful.
Consider a fixed p. All discontinuity points of all n curves lying in the closed interval [p/b1, (p + \)/bl ] are sorted into increasing order. Let Xj and xJ+l be two consecutive points in the sorted list of points. Then in the interval [xjt xj+, ] each of the -curves is just a line segment, expressible in the form b,u — c{, where c{ is a constant depending on i and j (and, of course, also on p).
The solution of the following system of linear inequalities in u is a (possibly empty) open subinterval of [x7-, xJ+1]:
Xj<U< xj+i ,
i (M - c{) < 1 ,
i= 1
(b, u - c{) + . . . + (bj-1 u - cj-,) < bjU - cj, i = 2,...,n.
A necessary and sufficient condition for two numbers u and m to constitute a trapdoor pair is the membership of u/m in a subinterval thus constructed, for some p and j. Indeed, the last inequalities express the super-increasing condition, and the inequality preceding the last the condition for the modulus being sufficiently large.
Thus, the second part of the algorithm investigates successively through pairs (p,j), where p is a candidate produced by the first part and j is an index of a point in the sorted list corresponding to p. The investigation is carried out until a nonempty interval is found. At least the trapdoor pair actually used by the cryptosystem designer corresponds to a nonempty interval.
The second part of the algorithm amounts to finding a rational number u/m from some nonempty interval we are considering. This is a problem in Diophantine approximation. The first part amounts to producing candidates p worth a further study, which is a problem of integer programming. Both techniques require only polynomial time. Recall also that the algorithm reports failure if more than r candidates p are generated in the first part. In the inequalities of the first part also a bound 8 is considered. It is estimated in [Sh2] that if we choose 8 < NfbJ2, then the probability for the algorithm to fail is at most (2/r)s_1. The degree of the polynomial expressing the running time of the algorithm is hard to estimate, as is the interrelation between the degree, the failure probability and the values of the three chosen constants <5, r and s.
From the point of view of decryption it does not make much difference if we do not obtain a super-increasing vector but rather a permutation of a super-increasing vector. The permuted version can be quickly sorted into increasing order. While we cannot analyze in polynomial time all n\ permutations of the given vector B, we can reduce the number of permutations by using the fact that a super-increasing vector is also an increasing one. This is done by making the intervals [x;, xj+smaller by including also the intersection points between pairs of curves (in addition to the discontinuity points of all curves). This increases the expected number of intervals from 0(n) to 0(n2). Within each new interval there is a specific vertical ordering of all curves. This ordering gives the only possible permutation of the arcomponents, provided the interval in question leads to success. The inequalities have to be modified because the super-increasing condition is not any more required.
Example 3.2. Our first illustration of the algorithm is very simple. The publicized vector is B = (7, 3, 2). Of course, it is very easy to handle this vector directly; it is even super-increasing in reverse order. However, in case of this vector all computations can be presented in great detail. This means that many details of the algorithm can be further clarified.
Consider the first part of the algorithm. There are two double inequalities
— 3 < 3p — Iq < 8, — 8 < 2p — Ir < 8 ,
where 1 < p < 6, I < q <2, r = 1. We are looking for values of p such that the inequalities are satisfied, for some q and r in their respective ranges. We still have to fix the value of the constant 8. The choice 8 = y/bl/2 = y/f/2 = 1.87 was recommended above. This choice produces no values of p. Indeed, in small examples any asymptotic result might be wrong. We intend to check through all values of p in the second part of the algorithm. The following table lists for each p the smallest value of 8 such that the above inequalities, where < is replaced by < , have a solution for some q and r. (Ir can of course be replaced by 7 because r = 1 is the only possible value.)
1 2 3 4 5 6
8 5 3 2 2 3 5
It will be seen below that even if we choose <5 = 2, we miss the correct p-value.
such that all of the three b,-curves are line segments btu — c{ in each subinterval. (As before, the superscript j indicates the interval.) We consider here open rather than closed intervals because no discontinuation point of some f>,-curve can give a trapdoor pair.
The inequalities to be considered, for each subinterval, in the second part of the algorithm are
(7ii - f) + (3m - /") + (2M - £"') < 1 ,
7m — f <3u — i" ,
(7u-i') + (3M-i")<2u-i'",
where the constants range over the values 0 < i" < 6, 0 < i" < 2, 0 < i'" < 1, depending on the subinterval. The inequalities can be written in the form
12 u < i,
4 u <j ,
| Thus, for the second part of the algorithm, we accept all p-values as candidates. This means that we divide the entire interval (0, 1) into subintervals |
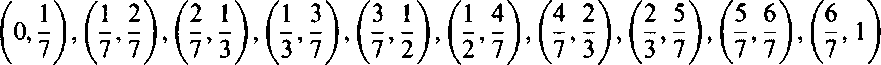
|
8m < k ,
where the new constants are obtained from the old ones: i = 1 + i' + i" + i'", j = i' — /", k = i" + i" — ("'. The following table lists the values of the constants in different intervals and tells, as regards each interval and each of our three inequalities, whether the inequality is satisfied in the whole interval (SAT), in some part of the interval (PART), or not satisfied in any point of the interval (NOT). Intervals are given by listing their right end point.
| Interval | 1/7 | 2/7 | 1/3 | 3/7 | 1/2 | 4/7 | 2/3 | 5/7 | 6/7 | |
| i'" | ||||||||||
| i | ||||||||||
| j | ||||||||||
| k | ||||||||||
| 12 u<i | PART | PART | NOT | NOT | NOT | NOT | PART | NOT | PART | NOT |
| 4 u < j | NOT | PART | SAT | NOT | SAT | NOT | SAT | NOT | PART | SAT |
| 8u < k | NOT | NOT | NOT | PART | SAT | NOT | NOT | NOT | PART | PART |
Clearly, NOT appears iff the inequality is not satisfied at the left end point of the interval. Similarly, SAT appears iff the inequality is satisfied at the right end point of the interval. An interval I generates trapdoor pairs iff either SAT or PART appears for each inequality. In such a case, the final interval is a subinterval of I.
In our illustration, the only such interval begins from 5/7. The right end point is 3/4. It turns out that all inequalities lead to the same right end point, which is not the case in general. By choosing the numbers 8/11,41/56, 61/84 and 223/308 from this interval, we obtain the super-increasing vectors
(1,2,5), (7,11,26), (7,15,38) and (21,53,138),
respectively. The modulus 11 is the smallest possible because there is no rational with denominator < 10 in the open interval (5/7, 3/4). Our second illustration is the publicized vector
B = (43,129, 215,473,903, 302, 561, 1165, 697, 1523)
already considered in Example 2.1. Now it does not make sense to write out a complete list of discontinuation points in any interval (p/43, (p + l)/43). For instance, the 1523-curve alone has 35 discontinuation points in such intervals. However, B contains enough cryptographic weaknesses for us to make various shortcuts in the algorithm.
The inequalities of the first part of the algorithm can now be written as
1129p — 43g| < <5, 1215p — 43r| < 8, |473p - 43s| < <5.
Since the numbers 129, 215 and 473 happen to be multiples of 43, we get p = 1 as a candidate even if we choose 5 = 0. We do not investigate other candidates and, thus, we are interested in the interval (1/43, 2/43). Consider discontinuation points of other curves in this interval. The one closest to the left end point of the interval is 36/1523. It is not necessary that the closest point is obtained using the greatest 6,-number but for this B it happens to be the case.
Our interval is now (1/43, 36/1523). In this interval the brcurves are
43 u — 1, 129M — 3, 215M — 5, 473 m — 11, 903M-21, 302 M — 7, 561M -13, 1165M- 27, 697M - 16, 1523M - 35 .
The inequality expressing the size of the modulus is
6011 m - 139 < 1, yielding u < 140/6011 .
Since 140/6011 < 36/1523, we get the new interval (1/43,140/6011).
We now list the inequalities expressing the super-increasing condition. The left column gives the inequality and the right column the solution.
| M > 1/43 , M > 1/43 , u > 1/43 , M > 1/43 , M < 34/1461 , M < 35/1504, u < 34/1461 , M < 72/3094 , M < 69/2965 . |
129M - 3 > 43M - 1 , 215M-5> 172M-4,
473u — 11 > 387M-9, 903M - 21 > 860M - 20 , 302m — 7 > 1763M-41 , 561 u- 13 > 2065M -48, 1 165M — 27 > 2626M — 61 , 697m- 16 > 3791M-88, 1523m- 35 > 4488M- 104
The first four inequalities are satisfied in the whole interval, whereas the remaining five restrict the right end point of the interval. The smallest among the upper bounds obtained for u is
72/3094 = 36/1547 .
Thus, we obtain finally the interval (1/43, 36/1547). Choosing the number 37/1590 from this interval, we obtain the super-increasing vector of the cryptosystem designer mentioned in Example 2.1. Choosing the number 72/3095, we get the super-increasing vector
(1,3, 5,11,21,79,157,315, 664,1331).
The reader might want to compute the super-increasing vector obtained by choosing the number 720/30949 from our final interval. Our next illustration is the first publicized vector
B = (4579, 50316, 24924, 30908, 27110 , 17953, 32732, 16553, 22075, 53620)
considered in Example 3.1. This is much trickier than the vector B from Example 2.1 considered above. We do not go into any details of the first part of the algorithm. We only mention that p = 88 is a candidate generated. This leads to the interval (88/4579, 89/4579). The three leftmost discontinuation points of our curves are in increasing order of magnitude
594/30908, 479/24924 and 967/50316 .
In the interval (88/4579, 594/30908) the curves have the form
4579 m — 88, 50316m — 966, 24924u - 478 , 30908m - 593, 271 10M - 521, 17953u - 345, 32732u - 629 , 16553 m - 318, 22075 u - 424, 53620 u - 1030 .
The sum of these expressions should be less than 1. This leads to the inequality
280770u < 5393 ,
which is not satisfied for any u in the interval. We have to consider next the subintervals
(594/30908, 479/24924) and (479/24924, 967/50316).
The right side of the inequality above is in these subintervals 5394 and 5395, respectively. (This is due to the fact that the constant in the 30908- and 24924- curves is increased by 1.) But still the inequality is not satisfied by any m in the subinterval.
We proceed to study the interval
(967/50316, 1031/53620)
whose right end point is the next discontinuation point. In this interval the above inequality expressing the size requirement of the modulus gets the form
280770m < 5396, yielding u < 2698/140385 .
This leads to the new interval
(967/50316, 2698/140385).
We now write the inequalities expressing the super-increasing condition. As before, the left column gives the inequality and the right column the solution
50316m - 967 > 4579m - 88 , u > 879/45737 ,
24924u - 479 > 54895m - 1055 , u < 576/29971 ,
30908m - 594 > 79819m - 1534 , u < 940/48911 ,
271 10m - 521 > 1 10727m - 2128 , u < 1607/83617 ,
17953m - 345 > 137837m - 2649 , u < 2304/119884 ,
32732m - 629 > 155790m - 2994 , u < 2365/123058 ,
16553m - 318 > 188522m - 3623 , u < 3305/171969 ,
22075 m - 424 > 205075 m - 3941 , u < 3517/183000 , 53620m - 1030 > 227150m - 4365 , u < 3335/173530 .
Only the first inequality has influence on the end points of our interval. Hence, our final subinterval will be
(879/45737, 2698/140385).
The interval is very tight: the end points differ by 1 on the 9th decimal only. The number 1061/55207 corresponding to the trapdoor pair of the cryptosystem designer lies in this interval. It is interesting to note also that neither one of the end points of the final interval is a discontinuation point and that the left end point lies quite far from our original left end point 88/4579.
Our final illustration deals with the second publicized vector B of Example 3.1. Without going into any details, we mention that the following interval is obtained:
/410868073108917982154 410868073109349502042
V1264891196933908912166 ' 1264891196933908912166
The original u/m lies in this interval, and so does
u' __ 410868073109000000000 m' ~ 1264891196933908912166
We reduce the quotient u'/m' and obtain the super-increasing vector A' with
a[ = 450448325606142
a'2 = 454908210018084
a'i = 918736188860052
a'4 = 1837472377720104
a's = 3670484871028266
a'6 = 26182899405826276
a'n = 71194348822186470
a's = 142388697644372940 a'g = 303619324952515624 a io = 607234190020619306 a'n = 1233314769589420298 a\2 = 2466629539178840596 a[ 3 = 4933254618473269250 a'14 = 9866513696830950442 a; 5 = 19751855943672434802 a'i6 = 39522549357124227406 a'17 = 79045103174132866754 a'i 8 = 158109039358160679368 a'19 = 316218087636090182620 «2o = 632436175272180365240 .
3.3 Theory of Reachability
Does a given knapsack vector B result from some super-increasing vector by strong modular multiplication or perhaps by a sequence of strong modular multiplications? If it does, we would like to know such a super-increasing vector, as well as the multipliers and moduli involved. These are the issues investigated in this section.
The setup will be quite general. There will be no restrictions concerning the sizes of the components with respect to n. The algorithms will be deterministic. The complexity depends on how the size of the input is defined. It is to be emphasized that the problems mentioned above are quite different from the knapsack problem itself. For instance, the problems do not become easy if the number of the components of B is bounded by a constant k. For these problems, it is still not sufficient to make 2* experiments. In general, if the problems above have been settled, the corresponding knapsack problems will be easy.
By definition, a knapsack vector B is super-reachable iff there is a super- increasing A such that B results from A by strong modular multiplication. For r > 1, the vector B is r-hyper-reachable iff there is a sequence of vectors A0,Al,. . . ,Ar = B such that A0 is super-increasing and, for each i = 0,. .., r — 1, Ai+1 results from At by strong modular multiplication.
Clearly, the notions of super-reachability and 1-hyper-reachability coincide. A vector may be defined in a way showing it to be r-hyper-reachable, r > 1, but the vector may still be super-reachable. For instance, in the fundamental paper [MeH] about knapsack-based cryptosystems, the vector B = (25, 87, 33) is obtained from the super-increasing vector A = (5,10,20) by two strong modular multiplications, with respect to the modulus-multiplier pairs (47,17) and (89, 3). It is also shown that B cannot be obtained from A by one strong modular multiplication. However, B is super-reachable because it is obtained from (2, 3,66) by strong modular multiplication with respect to the pair (99,62).
We require strong modular multiplication because then Lemma 3.1 becomes available. If we have only modular multiplication, it is not guaranteed that a solution of (B, [1) equals the only solution of (A, a), where a results from ft by the corresponding inverse modular multiplications. This conclusion can be made if the original multiplications are strong, even if there are several of them.
The following result is a basic tool in constructing examples of vectors that are not r-hyper-reachable.
Theorem 3.1. Every r-hyper-reachable vector is injective. Hence, every super-reachable vector is injective.
Proof. The theorem is a consequence of the following facts (i) and (ii).
(i) Every super-increasing vector is injective. Indeed, the algorithm described in Example 2.1 shows that any knapsack problem (A, a), where A is super-increasing, possesses at most one solution.
(ii) Strong modular multiplication preserves injectivity. Assume that B results from A by strong modular multiplication with respect to the pair (m, t). Assume, further, that BC = BC' for some bit vectors C and C'. Clearly, A results from B by modular multiplication (m, u), where u is the inverse of t. Because we have uBC = uBC' by assumption, we have also AC = AC' (modm). Since m exceeds the sum of the components of A, this congruence must be an equation: AC = AC'. By (i) we conclude that C = C' and, hence, B is injective. □
For instance, if some component in a vector equals the sum of some other components, the vector cannot be r-hyper-reachable.
Consider a knapsack vector A = (au..., an), an integer m > max A and a positive integer t < m such that (t, m) = 1. The growing sequence associated with the triple (A, t, m) is the sequence of triples (A(k), t,m + kt), k = 0, 1,2,..., where
A(k) = (al+k• [tajm],.. .,an + k-[tajm~\).
Thus, the growing sequence begins with (A, t, m). The terms multiplier and modulus refer also to the number t and m + kt in the triple (A(k), t,m + kt).
For instance, if A = (1, 2, 3), t = 4, m = 5, then the growing sequence begins with the triples
((1,2, 3), 4, 5), ((1,3, 5), 4, 9) and ((1, 4, 7), 4, 13).
If A = (1,4, 7), t = 3, m = 8, then the growing sequence is
((1, 4 + k, 1 + 2 k), 3, 8 + 3 k), k = 0,1,2,... .
A number i, 2 < i < n, is termed a violation point in a knapsack vector A iff
i- 1 < Z Cj ■
j= 1
Thus, the i-th component of A violates the requirement of A being super-increasing. If A is increasing, every violation point i in A satisfies i > 3.
The goal of a triple (A, t, m) is the first triple (/t(/c), t,m + kt) in the growing sequence such that A(k) is super-increasing and m + kt is greater than the sum of the components of A(k), provided such triples exist. Clearly, a triple can be its own goal and some triples have no goal. In particular, if A is not increasing, then (A, t,m) cannot possess a goal. This follows because a, > ai+1 implies that \tajm] > [fa1+1/m] and consequently, for all k,
at + k- [tajm] > a, +1 + k • [tai+l/m] .
Date: 2015-02-16; view: 829
| <== previous page | | | next page ==> |
| Chapter 3. Knapsack Systems 1 page | | | Chapter 3. Knapsack Systems 3 page |