
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Chapter 3. Knapsack Systems 1 page
3.1 A Trapdoor is Built
Public-key cryptosystems based on the knapsack problem were already briefly discussed in Example 2.1 in Chapter 2. It was also pointed out that knapsack systems are very suitable for illustrating all basic ideas behind public-key cryptography. The setup is also versatile enough to produce new variants to avoid cryptographic weaknesses.
Mathematical techniques will be used in this and later chapters to a larger extent than in Chapters 1 and 2. All the necessary tools will be summarized in the appendices. Fundamentals of the theory can also be understood without entering the mathematical developments.
This section presents the basic knapsack system in more details than Example 2.1. Shamir's cryptanalytic attack is described in Section 3.2. Section 3.3 deals with a general theory of reachability, applicable to both simple and composite knapsacks. Interesting variants of knapsack systems will be presented in Section 3.4. The final Section 3.5 deals with systems based on dense knapsacks.
We are now ready to go into definitions. A knapsack vector A = (al5. . ., an) is an ordered n-tuple, n > 3, of distinct positive integers a{. An instance of the knapsack problem is a pair (A, a), where A is a knapsack vector and a is a positive integer. A solution to (A, a) is a subset of A whose elements sum up to a. (Since we are talking about a subset, each a, appears in the sum at most once.) Knapsack problems are sometimes called also subset sum problems.
The most common variant of the knapsack problem is to tell whether or not a given instance (A, a) possesses a solution. A variant used in cryptography is to produce a solution for a given instance (A, a) when it is known that a solution exists. Both of these variants are iVP-complete. There are also variants that are not even in NP.
A knapsack vector A is used to encrypt a block C of n bits by summing up such components of A that 1 appears in the corresponding position in C. If the sum is denoted by a, then decryption amounts to finding C from a, or from A and a. if we are dealing with a public-key cryptosystem. The latter possibility is just the cryptographic variant of the knapsack problem.
Equivalently, we may view C as a column vector of bits. Then a equals the product AC.
As an illustration, assume that n = 6 and A = (3,41,5,1,21,10). Then (1,1,0,0,1,0) and (1,0,1,1,0,1) are encrypted as 65 and 19, respectively. For this A, all cryptotexts a are numbers < 81. At most one plaintext corresponds to each cryptotext.
For A = (14, 28, 56, 82, 90, 132, 197, 284, 341, 455), the cryptotext a = 515 has exactly three corresponding plaintexts
(1,1,0,0,0,1,0,0,1,0), (0,1,1,0,1,0,0,0,1,0), (1,0,0,1,1,1,1,0,0,0) .
This is seen immediately by reading A from right to left, for instance, 455 cannot appear in the solution because it is not possible to express 60 = 515 — 455 as a sum. Similarly, the cryptotext a = 516 has no corresponding plaintext. Now it is easy to see that none of the last four numbers in A can appear in the sum, whereas the sum of the remaining numbers is too small. For a = 517, the only corresponding plaintext is (1,1,1,0,1,1,1,0,0,0). Examples like this illustrate the obvious fact that cryptanalysis arising from some instances of the knapsack problem can be easy.
Since uniqueness of decryption is desirable, the knapsacks vectors A should have the property that, for every a, all instances (A, a) possess at most one solution. Such knapsack vectors A are referred to as injective in the sequel. This terminology is very natural because the injectivity of A means that the function induced by A, defined in Example 2.1, is injective. Of the two /l's considered above the first is injective, whereas the second is not.
For some vectors A, all instances (A, a) are easy to solve. We have already seen in Example 2.1 that super-increasing vectors possess this property. A two-way cryptosystem can be based on such vectors in an obvious fashion: both the sender and receiver know the vector A. On the other hand, if a vector B is publicized as an encryption key, then the legal receiver must have some secret trapdoor information for transforming B and the cryptotext into an easy instance of the knapsack problem. We already indicated in Example 2.1 how this can be done using super-increasing vectors. The construction will now be given in a somewhat more detailed form.
A knapsack vector A = (a,,. . ., a„) is increasing (resp. super-increasing) iff
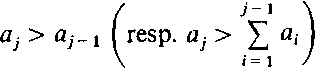
|
holds for all j = 2,..., n. Clearly, every super-increasing vector is increasing. For a knapsack vector A we define
max A = max (aj | 1 <j<n).
Let x be a nonnegative number. We denote by [x] the integer part of x, that is, the greatest integer < x.
For integers x and m> 2, we denote by (x, mod m) the least nonnegative remainder of x modulo m. It is easy to see that
(x, mod m) = x — [x/m] ■ m
This equation will be often, especially in Section 3.3, written in the form
x = (x, mod m) + [x/m] • m .
We now define two variants of the notion of modular multiplication. Consider a knapsack vector A, an integer m > max A and a positive integer t < m such that the greatest common divisor (t,m)= 1. If B = (b1,. . ., b„) is a vector such that
bj = (tah mod m), for i = 1,. . ., n ,
we say that B results from A by modular multiplication with respect to the modulus m and multiplier t or, briefly, with respect to the pair (m, t). The condition (f, m) = 1 guarantees the existence of an inverse t'1 = u such that
tu = 1 (mod m)
and 1 < u < m. This implies that also conversely A results from B by modular multiplication with respect to m and u. (Clearly m > max B because every b, is reduced modulo m.)
If above the condition m > max A is replaced by the stronger condition
n
m > Y, ai> we say that B results from A by strong modular multiplication with
;= i
respect to m and t. Observe that now we cannot conclude that A results from B by strong modular multiplication with respect to m and u because the inequality
n
m> Y, bi does not necessarily hold. Of course, A results from B by modular
i = 1
multiplication with respect to m and u.
A cryptosystem designer now chooses A, t, m, B such that A is super-increasing and B results from A by strong modular multiplication with respect to m and t. B is publicized as the encryption key, and n-bit blocks are sent to the designer as numbers fi obtained from B in the way described above. An eavesdropper has to solve the instance (B, ft) of the knapsack problem. The designer computes a = (uf), mod m) and solves the instance (A, a). Why this works is summarized in the following lemma.
Lemma 3.1. Assume that A = (a1,. . . ,a„) is super-increasing and B results from A by strong modular multiplication with respect to m and t. Assume further that u = t~l (mod m), [i is arbitrary and a = (ufl, mod m). Then the following assertions hold true, (i) The knapsack problem (A, a) is solvable in linear time. If a solution exists, it is unique, (ii) The knapsack problem (B, fi) has at most one solution, (iii) If a solution to (B, ft) exists, it equals the unique solution to (A, a).
Proof, (i) It was shown in Example 2.1 that every knapsack problem with a super- increasing A can be solved in linear time by reading through A once from right to left. The method shows that there can be at most one solution, (ii) and (iii) Assume
that an n-bit vector D is a solution to (B, /?), that is, BD = p. Consequently,
a = up = uBD = u(tA)D = AD (modm) .
Since m exceeds the sum of the components of A, we must have AD < m. Since also a < m, by the definition of a, we conclude that a = AD. Thus, D equals the unique solution to (A, a). This shows (iii). Since we started with an arbitrary solution to (B, P) and showed that it equals the unique solution to (A, a), we have established also (ii). □
In our cryptographic application of Lemma 3.1 we know that (B, P) has a solution: P was computed in a way to guarantee this.
Example 3.1. Our first illustration is still manageable with a pocket calculator. Let n = 10 and consider the super-increasing vector
A = (103, 107, 211, 430, 863, 1718, 3449, 6907, 13807, 27610).
Choose the modulus m = 55207 which is greater (by two) than the sum of the components of A. Choose further the multiplier t = 25236. Then (t, m) — 1 and t~l = u= 1061. Indeed,
1061-25236 - 1 =485-55207 . As a result of the strong modular multiplication we now get
B = (4579, 50316, 24924, 30908, 27110, 17953, 32732, 16553, 22075, 53620) . For instance,
25236-103 =4579 + 47-55207 and 1061-4579 = 103 + 88-55207, 25236-1718 = 17953 + 785-55207 and 1061-17953 = 1718 + 345-55207, 25236-27610 = 53620 + 12620-55207 and 1061-53620 = 27610 + 1030-55207 .
The vector B is the public encryption key, whereas the items A, t, u, m constitute the secret trapdoor. Of course, the knowledge of m and either t or u enables one to compute the other items immediately.
Let us now use the public key B and encrypt the plaintext IN FINLAND CHILDREN USED TO BE BORN IN SAUNA EVEN TODAY INFANT MORTALITY IS IN FINLAND LOWEST IN THE WORLD. We use first the numerical encoding, where the space between words gets the value 0 and the letters A Z the values 1-26. The numerical encoding is expressed in bits. In fact, a complete list of the bit values was given in Example 2.1. Since B can be used to encrypt blocks of ten bits, our plaintext has to be divided into blocks consisting of two characters each. In what follows, we give first a plaintext block, then the numerical encoding and, finally, the encryption of the block as a decimal number. The cryptotext consists of the 53 numbers thus obtained, written one after the other so that individual numbers are distinguishable.
| I N | OHIO | ||
| F | |||
| I N | oino | ||
| LA | |||
| ND | oino | ||
| C | |||
| H I | |||
| LD | |||
| R E | |||
| N | |||
| U S | |||
| ED | |||
| T | |||
| O | |||
| B E | |||
| B | |||
| OR | |||
| N | oino | ||
| I N | OHIO | ||
| S | |||
| AU | |||
| N A | OHIO | ||
| E | |||
| V E | |||
| N | OHIO | ||
| TO | |||
| DA | |||
| Y | |||
| I N | OHIO | ||
| FA | |||
| NT | OHIO | ||
| M | |||
| OR | |||
| T A | |||
| L I | |||
| T Y | |||
| I | |||
| S | |||
| I N | OHIO |
| F | |||
| I N | oino | ||
| LA | |||
| ND | |||
| L | |||
| OW | |||
| E S | |||
| T | |||
| I N | oino | ||
| T | |||
| H E | |||
| W | |||
| OR | |||
| LD |
We decrypt the first number 148786. Note first that
1061 • 148786 = 2859 • 55207 + 25133.
Consider the knapsack problem (A, 25133). The solution is obtained by scanning A once from right to left. Whenever the number at hand is at least the currently scanned component of A, we get the bit 1 and the new number is obtained by subtracting the component from the number previously at hand. Otherwise, we get the bit 0 and the number at hand remains unaltered. The result can be expressed as follows.
| Number Component of A Bit
|
The original bit vector, from which the plaintext IN results, can be read from the last column bottom up. In the decryption of the second number 38628 we obtain first 20714 which is treated similarly, and so forth.
A further remark is in order. Assume that we try to proceed in the reverse order. Consider the plaintext block OR appearing three times. Encrypt it first with A, yielding 17136. Apply strong modular multiplication with respect to 55207 and 25236, yielding 7665. But (B, 7665) clearly possesses no solution. The simple explanation is that we cannot deduce an equation from a congruence (as in the proof of Lemma 3.1) because m is smaller than the sum of the components of B. Indeed,
7665 ee 173286 (mod 55207),
and we should operate with 173286.
Our second illustration is too big for a pocket calculator but still too small for real encryption. Realistic examples are very likely to become completely unreadable. The computations here, as well as in the final illustration in Example 4.1, are due to Kimmo Kari.
Let now n = 20. Choose the modulus and multiplier
m = 53939986 and t = 54377 ,
yielding t ~1 = u = 17521047. The super-increasing A is defined by:
| = | ||
| = | ||
| a3 | = | |
| a4 | = | |
| a5 | = | |
| a6 | = | |
| an | = | |
| <*8 | = | |
| ag | = | |
| flio | = | |
| an | = | |
| a!2 | = | |
| "13 | = | |
| a14 | = | |
| a,s | = | |
| f 16 | = | |
| an | = | |
| <*18 | = | |
| a19 | ||
| «20 |
Strong modular multiplication gives now the following publicized vector B:
b, = 5492077
b2 = 5546454
b3 = 11201662
b4 = 22403324
b5 = 44752271
b6 = 35618933 b-, = 17189126 bs = 34378252 b9 = 14870895 bl0 = 29687413 bu= 5543594 bl2 = 11087188 b13 = 22119999 bu = 44294375 b15 = 34540010 b16 = 15140034 ft, 7 = 30334445 fe18 = 6674527 fe19 = 13457808 *>20 = 26915616
Let us encrypt the following plaintext about sauna: IF YOUR FEET CARRY YOU TO SAUNA THEY SURELY CARRY YOU BACK HOME IF SAUNA ALCOHOL AND TAR DO NOT CURE YOUR DISEASE IT MUST BE FATAL. As before, empty space is encoded as 0, and the letters A-Z get the numbers 1-26. Five bits per number are required in binary notation. Since n = 20, four plaintext characters are encrypted at the same time. The encoding, divided into sequences of 20 bits, looks as follows.
| I F Y | ||||
| OUR | ||||
| FEET | ||||
| CAR | ||||
| R Y Y | ||||
| OU T | ||||
| O S A | ||||
| UNA | ||||
| THEY | ||||
| SUR | ||||
| ELY | ||||
| C A R R | ||||
| Y YO | ||||
| U B A | ||||
| CK H | ||||
| OME | ||||
| I F S |
| AUNA | OHIO | |||
| A LC | ||||
| OHO L | ||||
| AND | OHIO | |||
| TAR | ||||
| DO | ||||
| NOT | oino | |||
| CURE | ||||
| YOU | ||||
| R D I | ||||
| SEAS | ||||
| E I T | ||||
| MU S | ||||
| T BE | ||||
| FAT | ||||
| A L |
The cryptotext consists now of the following numbers (see the remark below at the end of Example 3.1):
| 1 3 | |||||||
| 1 7 | |||||||
| 1 9 | |||||||
| 1 0 | |||||||
| 2 1 | |||||||
| 1 8 | |||||||
| 1 5 | |||||||
| 1 6 | |||||||
| 2 2 | |||||||
| 2 0 | |||||||
| 1 6 | |||||||
| 1 4 | |||||||
| 1 8 | |||||||
| 1 2 | |||||||
| 2 0 | |||||||
| 1 1 | |||||||
| 1 4 | |||||||
| 2 4 |
The legal recipient multiplies these numbers by u (mod m), and goes back to the super-increasing A. For instance, the multiplication of the first number gives 15488011. When solving this with respect to A, we get similarly as in our first illustration:
| Number Component of A Bit
|
Our encryption procedure in this second illustration was exceptional: the order of the components of B was reversed before encryption. Thus, to get the first encrypted number 134452701 we formed the sum b19 + bl6 + bti + b12 + b5 + i>4 + fc,. This procedure follows the analysis of A from right to left in the table above. However, the procedure will not be repeated in the sequel because it is unnatural from the point of view of vector multiplication. □
3.2 How to Find the Trapdoor
We face the following cryptanalytic task. A knapsack vector B = (blt. . ., bn) is known to us. B is used as a public encryption key in the manner described above. We also know that B is obtained by strong modular multiplication from a super- increasing vector A, with respect to a modulus m and multiplier t. All of the items A, m and t are unknown to us. We want to find them. What interests us most directly is to find m and t~l =u (modm). Knowing m and u we can immediately compute A and decrypt any cryptotext. The computation of u from t, or vice versa, amounts to one application of Euclid's algorithm and can be done fast.
The cryptanalytic setup here is encryption key only. Often this means that more time is available because the analysis of the system can be carried out before important cryptotexts have been sent.
This section discusses A. Shamir"s cryptanalytic approach. The resulting algorithm runs in polynomial time. However, it is to be emphasized that a classification of cryptosystems into bad and good is overly simplified if it focuses only on the condition whether or not a polynomial time algorithm for the cryptanalysis is known. The degree of the polynomial is very important in cryptography. Moreover, as we have already emphasized, knapsack systems are very versatile for producing modifications to overcome known cryptanalytic attacks.
When we say that an algorithm runs in polynomial time, we have to be careful in defining the size of an instance B, the algorithm being polynomial with respect to the size. We have to consider a family of knapsack vectors B whose sizes grow to infinity. There are two parameters contributing to the size of a vector B: the number n of the components and the sizes of the individual components bt. If either one of the parameters is kept bounded from above, the resulting knapsack problems can be solved trivially in polynomial time.
Indeed, if each bt in every vector considered is less than some constant C, the total number of vectors is finite and, hence, there is some fixed time bound such that every knapsack problem considered can be solved within this time bound. On the other hand, if always n < C then every knapsack problem considered can be solved in linear time, where the coefficient is the constant 2C.
Date: 2015-02-16; view: 874
| <== previous page | | | next page ==> |
| Chapter 2. The Idea of Public Keys | | | Chapter 3. Knapsack Systems 2 page |