
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Chapter 3. Knapsack Systems 3 page
Returning to the two examples considered above, i = 3 is a violation point in the initial vector of the first sequence. The third triple is the goal of the sequence. The second sequence possesses no goal because the modulus will never become big enough.
Next we define a notion in some sense dual to that of a growing sequence. Let {A, t, m) be a triple defined as in connection with growing sequences. The diminishing sequence associated with the triple (A, t, m) is the sequence of triples (A( — k), t,m — kt), k = 0, 1, 2,..., where the vectors A( — k) are defined by descending induction as follows. A( — 0) = A. Assume that A( — k) = (dt,. . . ,dn) has been defined and that we still have m — kt > max A ( — k). (The inequality holds for k = 0, by the choice of the original triple.) Then
A{-k-l)^(d1- [tdl/(m - ktU,. ..,d„- [tdj(m - let)]).
Diminishing sequences are always finite, whereas growing sequences are infinite. However, in the sequel only finite initial segments of growing sequences will be of interest. We will now develop the technical tools needed for the algorithms. We begin with properties of growing sequences. In Lemmas 3.2-3.4, the notation A, t, m, A(k) is the same as in the definition of a growing sequence.
Lemma 3.2. If A is increasing or super-increasing, then each vector in the growing sequence associated with (A, t, m) is increasing or super-increasing, respectively.
Proof. The inequality a,-_ i < at implies the inequality [taj-1 /m] < [tajm], Hence, if A is increasing then so is every A(k).
Assume, next, that
i- I
| i - 1 I Ltaj/ni] < j= i |
| ^t X aj)Im |
I ai< ai ■
j= i
Consequently,
< [tajm] .
This implies that, whenever A is super-increasing, then so is every A(k). □
Lemma 3.3. If B = . . . ,b„) results from A by modular multiplication with respect to (m, t), then B results also from every A {k) by modular multiplication with respect to (m + kt, t). This holds true also if "modular multiplication" is replaced by "strong modular multiplication".
Proof. We infer by the assumption:
bj = (ta;, mod/w), for 1 < / < n .
Clearly, (r, m + kt) = 1. For all k,
t(a, + k • [tajm] ) = />, + [tajm] • m + [tajm] • /cf
= h + [tajm] (m + kt).
Since bt < m + kt, we conclude that
(f(a; + k • [tajm]), mod {m + kt)) = bt.
This means that B results from A(k) by modular multiplication with respect to (m + kt, t).
Assume that B results from A by strong modular multiplication with respect to (m, t). This implies that
n
I a, < m .
i = 1
Consequently,
n n
X (af + kltajmj) < m + £ i= i ;=i
< m + k[t(a1 + . . . + a„)/m] < m + k • [t] = m + kt .
We may infer that B results from A(k) by strong modular multiplication with respect to the modulus m + kt and multiplier t. □
It is an immediate consequence of Lemmas 3.2 and 3.3 that every super- reachable vector can be obtained from infinitely many super-increasing vectors by strong modular multiplication. (The special case, where [tanjm\ = 0 and, thus, always A{k) = A, can be easily handled separately.)
We now investigate the question of which triples (A, t, m) possess goals. Recall that every violation point i in A satisfies
(*) ai<a1 + ... + ai-l .
Assume that also
(*)' Itajm] + . . . + [ffli-i/m] < [tajm] .
Observe that (*) and (*)' are by no means contradictory, even if we have a strict inequality in (*). The smallest integer x such that
i - 1 i - 1
Z ai + x I [tajM < ai + x[tajm]
| I - /([»] - I [taj/m] |
j= l i= l
is called the rescuer of i. Explicitly,
/ / 'z.1 V
+ 1 .
j=i ' 1- By (*) and (*)', x is a positive integer.
We consider, next, the situation where the modulus is not big enough:
m< 2^0;.
i = 1
Assume that also
(**y "
Z [tfl,/m] < t .
i= 1
Then the smallest integer y such that
n n
X>i + y Z Ltajm] <m + yt
i = 1 i = 1
is called the rescuer of m. An explicit expression for y, corresponding to the one written for x above, can be easily given.
If (*)' holds for every violation point / in A, then the rescuer of A is defined to be the maximum of the rescuers of all violation points /'.
It is important to notice that if i" is rescued by k', that is, i" is not a violation point in A(k'), then i' is not a violation point in any <4(/c), k > k'. Hence, if we have rescued several numbers (possibly including m), then we may go on further in the growing sequence until all of them have been rescued (if ever). For the sake of completeness, we say that 0 is the rescuer of i (resp. m) if (*) (resp. (**)) does not hold.
Lemma 3.4. A triple (A, t, m) possesses a goal iff{*)' holds whenever (*) holds and, moreover, (**)' holds in case (**) holds. If these conditions are satisfied, the goal is (/l(fc0), t,m + k0t), where k0 is the maximum of the rescuers of A and m.
Proof. If k0 is defined as in the statement of the lemma, then A(k0) is super- increasing (because it has no violation points) and m + k0t is greater than the sum of the components of /4(fc0). The definition of k0 guarantees that we obtain the smallest number satisfying these conditions. On the other hand, if some i satisfies (*) but in (*)' we have > instead of < , then i is a violation point in every A(k). Similarly, if (**) holds but (**)' does not hold then, for all k,
Z (a,- + k[tajm]) > m + kt.
Hence, the modulus is too small in every triple of the growing sequence. □
We now give some illustrations. In the following table A, t, m, B and the goal are listed. Here B results from A by modular multiplication with respect to (m, f). The goal always gives items showing that B is super-reachable. If no goal exists, we use the abbreviations NR(i = i") and NR(m) to mean that there is no rescuer for a violation point i" or modulus m, that is, (*)' or (**)' is not satisfied. In some cases there may be several such failures.
Example 3.3.
|
| k = 1 rescuer of / = 3. □ |
The first of our remaining three lemmas deals with an interplay between the multiplier and the modulus. We then discuss properties of diminishing sequences. Finally, growing and diminishing sequences are tied together. We say that B is (A, t, m)-super-reachable iff A is super-increasing and B results from A by strong modular multiplication with respect to the modulus m and multiplier t.
Consider a triple (A,t,m), where A = (a1;. . ., aj is a knapsack vector, m > max A, t < m and (t, m) = 1. The triple (A,, t,, m,), where
m, = t, t, = ( — m, mod t), ={itajm\,. . ., \ta„/m~\), is called the transposed version of (A, t, m).
Lemma 3.5. Assume that (A,, t,, mt) is the transposed version of (A, t, m). If B results from A by modular multiplication (resp. strong modular multiplication) with respect to (m, t) and max B < t, then B results also from A t by modular multiplication {resp. strong modular multiplication) with respect to (ml5 r,). If B is super-reachable, then B is (A', t', m')-super-reachable with t' < maxB.
Proof. Clearly, t, < t. We may repeat the construction of replacing a triple by its transposed version until a triple with t' < max B is reached.
Assume that B results from A by modular multiplication with respect to (m, t) and t > max B. Consequently, (ta^ mod m) = bt, for 1 < i < n. This implies that
fcj [ta,/m] = i>, — tat = bt (mod t).
Since bt < max B < t, we may write further
(f! [;a,/m], mod t) = bt,
which shows that B results from Al by modular multiplication with respect to (m,, f,). Also the claim concerning strong modular multiplication follows because
n
if m > Y at> ^en
i= 1
n n
' > Y tajm > Y l»] .
i = i ; = I
To prove the last sentence of Lemma 3.5, it suffices to show that if A is super-increasing then so is A,. The assumption of A being super-increasing implies, for 2 < i < n,
i- 1
Y tdj/m < tajm . j= i
Hence,
n I Itaj/ni] < [tajni] .
j= i
Assume that we have equality in (*). Then
i
Y mftflj/m] = m[ta(/m]
i= i
and consequently,
i- 1
Y (taj - bj) = ta, - bt,
j= i
which can be written in the form
h. - lhj = tU - Z a) ■
j=1 V 7=1 /
Since the coefficient of t is positive, we infer
i- 1
t <bt- Y < b{ < max B .
j= i
Since this contradicts the assumption t > max B, we must have strict inequality in (*). Since i was arbitrary, we conclude that A1 is super-increasing. □
As an illustration, we observe that the vector B = (46,45,40,30) is ((4,5,10,20), 49,50)-super-reachable. By Lemma 3.5, it is also super-reachable from each of the triples
((3,4,9, 19), 48,49), ((2, 3, 8,18), 47, 48) and ((1,2, 7,17), 46,47).
In the last triple the multiplier is < max B. We now discuss diminishing sequences.
Lemma 3.6. Assume that B results from A by modular multiplication with respect to (m, t) and that, furthermore, m > 2 max B and t < max B. Then B results also from A( — 1) by modular multiplication with respect to (m — t,t). Moreover, if A is increasing then so is A( — 1).
Proof. We use our customary notation A = A( — 0) = (a,,. . . ,a„) and B = (bt,..., bn). Then the i-th component of A( — 1), 1 < i < n, is
"i - [tajm] •
Multiplying this by f and using our assumption we obtain
ta, — t[tajm] = b, + m[tajm] — t[tajm] = bi + (m - t)[tajm] = fr,(mod(m - f)).
Because by our assumptions m — t > maxB > b:, we obtain (t(a, - [tajm]), mod(m - t)) = .
Observe that
(*) m>2t, yielding m — t > t,
and clearly (t, m — t) = 1. The first assertion now follows if the new modulus is big enough. Assume the contrary: a, — [tajm] >m — t, for some i. We multiply this by t, use the above expression for ta( and the assumption m > 2 max B, obtaining
t(m -t)< bi + (m — t) [tajm] < j + (m - t) [t«,/m] ,
from which
m/2 > (m - t)(t - [tajm]) ,
contradicting (*) because t > [tajm].
To prove the second assertion, we denote A( — 1) = (ej,. . .,e„). Let i be arbitrary, 1 <i<n— 1. Since A( — 0) is increasing,
ai+, = a, + a for some a > 1 .
Assume first that a > 1. Then
ei+1 = at + a - [t^ + a)/m]
> af + a - (1 + [tajm] + [ta/m]) = et + (a - 1) - [fa/m] > ef .
Here the first inequality follows because always [x + y] < [x] + [y] + 1, and the second because by (*)
[fa/m] < ta/m < a/2 . Assume, secondly, that a = 1. In this case [Ja/m] = 0. If
[t(ai + l)/m] = [tajm] ,
we obtain ei+l > ef. Hence, suppose that
(**) [t(a, + l)/m] = [tajm] + 1 .
Clearly, there are no other possibilities. (**) would imply that ei+1 = ef. Denote the right side of (**) by P + 1. Hence,
m/1 < tat < m(fi + 1) < t(a,- + 1).
Assume that ta,- < m(P + i). Hence by (*),
ta, + t < m^P + ^ + t = m(P + 1) + t - m/2 < m(P + 1),
a contradiction. Hence, fa,- > m(P + 2). But now
b, = tat - Pm> m/2 .
This implies that m < 2bt < 2maxB, contradicting our assumption. This shows that (**) cannot hold. □
Lemma 3.6 will be applied in the sequel to the triples of the diminishing sequence as long as we still have m — kt > 2 max B. In this way the modulus will be forced to become < 2 max B.
It is important to note that certain properties preserved by the growing sequences are not preserved by the diminishing sequences. A may be super- increasing although the other vectors in the diminishing sequence are not. For instance, choose
A = (1, 14, 23,66, 105), t = 87, m = 374 ,
implying that B = (87,96,131,132, 159) and, hence, t < maxB and m > 2 maxB. Now
A(- 1) = (1, 11, 18,51,81),
which is not super-increasing. Similarly, we see that (4, 3,2) results from (1,4, 7) by strong modular multiplication with respect to (13,4) but when we go to the first triple in the diminishing sequence, we observe that (4, 3, 2) does not result from (1, 3, 5) by strong modular multiplication with respect to (9,4) (although it results by modular multiplication as it should by Lemma 3.6). Such negative results are natural in view of our last lemma, Lemma 3.7, and reflect the fact that some properties are rescued from a certain point on in the growing sequence. The same properties are lost at this point in the diminishing sequence. The second assertion in Lemma 3.6 shows a property preserved by diminishing sequences. This assertion is not needed in the proof of our main result.
Lemma 3.7. Consider A, B, m and t satisfying the assumption of Lemma 3.6. Consider the growing sequence associated with (<4(— 1), t, m — t). Let (C, t, m), C = (c„ . . ., c„) be the first triple in this sequence. Then C = A.
Proof. As in Lemma 3.6, we denote A( — 1) = (e,,. . ., e„). We consider an arbitrary 1, 1 < i < n, and denote the components at, cit e, simply by a, c, e. By the
definition of growing and diminishing sequences, we have
c = e + [te/(m — f)] and e = a — [fa/m] . To prove that a = c (and hence also Lemma 3.7), we have to show that (*) Ue/(m - f)] = [ta/m] .
By Lemmas 3.3 and 3.6, we know that
ta = tc (mod m), yielding a = c (mod m) .
This implies that
(**) lte/(m - t)] = [ta/m](modm).
(**) can hold without (*) holding only in case that the absolute value of the difference between the two bracket expressions is a positive multiple of m. We prove that this is impossible by showing that both of the bracket expressions (which clearly are nonnegative) are less than m. Since m — t > max A( — 1) > e, we obtain
[te/(m - t)] < t < m .
The bracket expression on the right side of (**) is estimated by denoting t/m = x and using the principle [>>] < y. Therefore,
[ta/m] < xa = x(e + [ta/m]) < x(e + x(e + [ta/m]))
< x(e + x(e + x(e + [ta/m]))) < e{x + x2 + . . . + x") + xp[ta/m] <e/(l - x) + xp[ta/m] = me/{m - t) + xp[ta/m]
< m + xp[fa/m] .
This holds for arbitrarily large p, which means that the term xp[ta/m] can be made arbitrarily small. Consequently, [ta/m] < m. □
Lemma 3.7 can be used inductively in the same sense as Lemma 3.6. We may generate the diminishing sequence as long as the modulus satisfies the inequality m — kt > 2 max B. Once we have reached a value s with m — st < 2 max B, we may increase the modulus again by considering the growing sequence. Lemma 3.7 then tells us that the growing sequence coincides with the original diminishing sequence.
The following main result is now fairly obvious in view of the technical tools developed.
Theorem 3.2. A knapsack vector B is super-reachable iff, for some A, t < max B and m <2 max B, B results from A by modular multiplication with respect to (m, t) and the triple (A, t, m) possesses a goal.
Proof. The "if "-part follows by Lemma 3.3 and the definition of a goal. Lemma 3.4 gives a simple method for deciding whether or not a given triple possesses a goal.
For the "only if"-part, assume that B is super-reachable. By Lemma 3.5, B is (A, t, m)-super-reachable with t < max B. If m < 2 max B, we are finished. Otherwise, we form the diminishing sequence
(A( - k), t, m - kt), 0<k<s,
where 5 is the smallest integer such that m — st < 2 max B. By Lemma 3.6, B results from A( - s) by modular multiplication with respect to (m - st, t). By Lemma 3.7, the triple (A( — s), t, m — st) possesses a goal. □
The algorithm due to Theorem 3.2 can be described as follows. Given B, choose m satisfying max B <m <2 max B and u < m with (u, m) = 1. Check whether the vector A resulting from B by modular multiplication with respect to (m, u) is increasing and u~1 = t < max B. If not, choose another pair (u, m). Else check by Lemma 3.4 whether the triple {A, t, m) possesses a goal. If it does, B is super- reachable and the goal also gives a super-increasing vector, multiplier and modulus showing this. If (A, t, m) possesses no goal, another pair (u, m) is tried. When all possible pairs (u, m) have been tried without success, the algorithm terminates with the conclusion that B is not super-reachable.
Various shortcuts can be made in the choice of the pairs (u, m). The algorithm is deterministic and works for all instances, independently of any conventions concerning the size of the components of the vectors. Thus, also cheating which uses non-super-reachable vectors can be found out. As will be mentioned below, similar algorithms can be used to many other problems as well.
Example 3.4. We give some illustrations of the algorithm. Consider first B = (4, 1, 6). The following table lists all pairs (u, m), where m < 2 max B, u < m, (u,m)= 1, u ~ 1 < max B and the resulting A is increasing. Abbreviations are the same as in Example 3.3.
| u, m | t = u~l | A | Goal |
| 3, 11 | (1,3,7) | k = 1,(1,4,9), 4, 15 | |
| 9,11 | (3, 9, 10) | NR(i = 3), NR(m) | |
| 5,8 | (4, 5, 6) | NR(i = 3), NR(m) | |
| 2,7 | (1, 2, 5) | k = 2,(1,4,9), 4, 15 |
Thus, (4,1,6) is super-reachable. It is interesting to note that in both cases leading to success we obtain the same goal. It follows that, whenever (4,1,6) is (A, t, m)-super-reachable, then t > 4 and m > 15. Thus, it does not suffice to investigate moduli m <2 max B without considering growing sequences. Of course, m can be arbitrarily large in the growing sequence. Also t can be made larger by applying an argument similar to that used in Lemma 3.5 in the reverse order.
The vector B = (1,10, 8) is 2-hyper-reachable because it results from (1, 2,4) by two strong modular multiplications, first with respect to (8, 5) and then with respect to (12, 5). The following table shows that B is not super-reachable.
| m, m | t = u~l | A | Goal |
| 7, 20 | (7, 10, 16) | NR(i = 3), NR(m) | |
| 9, 20 | (9, 10, 12) | NR(i = 3), NR(m) | |
| 2, 17 | (2, 3, 16) | NR(m) | |
| 6,17 | (6, 9, 14) | NR(i = 3), NR(m) | |
| 5, 14 | (5, 8, 12) | NR(i = 3), NR(m) | |
| 3, 13 | (3, 4,11) | NR(m) | |
| 4, 11 | (4, 7, 10) | NR(i = 3), NR(m) | |
| 5, 11 | (5, 6, 7) | NR(i = 3), NR(m) |
Of knapsack vectors with all components < 4 exactly the following ones are super-reachable:
(2,4,3), (4,3,2), (1,2,4), (2,4,1), (4,1,2).
The study of (4, 3, 2) is interesting because it shows that one cannot reject non- injective candidates A in spite of Theorem 3.1.This is due to the fact that injectivity can be gained later on in the growing sequence.
We now return to Example 3.2 and show how some of the results can be obtained by the method of Theorem 3.2.
Consider B = (7, 3, 2). We saw that the number 61/84 is in the interval obtained. Since 73 is the inverse of 61, we conclude that B is ((7, 15, 38), 73, 84)-super- reachable. Here the multiplier is too big. Lemma 3.5 yields, in succession, the triples
((6, 13, 33), 62, 73), ((5, 11, 28), 51, 62), ((4, 9, 23), 40, 51), ((3, 7, 18), 29,40), ((2, 5, 13), 18,29), ((1,3, 8), 7, 18) .
In the last triple the multiplier t = 1 satisfies t < max B, and we cannot apply Lemma 3.5 further. However, we still have m > 2 maxB. But taking one step in the diminishing sequence we obtain the triple ((1, 2, 5), 7, 11). Consider, finally, the vector
B = (43, 129, 215, 473, 903, 302, 561, 1165, 697, 1523).
We computed in Example 3.2 the interval (1/43, 36/1547). Choosing the number u/m = 72/3095 from this interval, we get the super-increasing vector
A = (1, 3, 5, 11, 21, 79, 157, 315, 664, 1331).
Now t = 43 < max B but m > 2 max B. When we go two steps back in the diminishing sequence, we obtain the triple
| □ |
((1, 3, 5,11, 21, 77, 153, 307, 646, 1295), 43, 3009).
Now also m is within the size limits.
We call a vector B permutation-super-reachable iff some permutation of B is super-reachable. Cryptanalytic significance of permutation-super-reachable vectors was discussed earlier. As in Theorem 3.1 we can show that every permutation- super-reachable vector is injective. Conversely, by our theory it is easy to see that every injective (b1,b2,b3) is permutation-super-reachable.
Assume that B is super-reachable. Theorem 3.2 gives a method of finding the smallest m such that B is (A, t, m)-super-reachable, for some A and t. The multiplier t can be similarly minimized. By estimating the maximal number of steps in the growing sequence before the goal is reached, one can also compute an upper bound M, depending on B, such that B is super-reachable iff it is (A, t, m)-super-reachable with m < M. Using our lemmas one can also decide of a given pair (B, r) whether or not B is r-hyper-reachable and, if the answer is positive, produce the corresponding super-increasing vector, multipliers and moduli. More details about all of these matters are given in [Sa 4], It will be seen in the next section how one can choose an arbitrary starting vector if one uses sufficiently many strong modular multiplications to get the publicized vector.
3.4 Trying to Hide the Trapdoor Again
The last two sections in this chapter discuss variants of knapsack-based cryptosystems, exhibiting various methods to meet cryptanalytic attacks.
It has been emphasized already several times that some caution is needed in cryptography as regards arguments based on complexity theory. From a cryptographic point of view it does not prove much if it is shown that the worst instances of some problem are difficult but little or nothing is known about the average complexity of the problem. As regards algorithms running in polynomial time, the degree of the polynomial is important. Even if an expected cryptanalytic attack leads to an NP-complete problem, there might be other attacks that lead to easy problems. This point will now be illustrated using ideas based on knapsacks. The cryptosystem described will be partially public-key in that a knapsack vector A = (<*!,. . .,a„) is publicized, whereas there is also a secret key K =(kl,. . ., fc„) with /Cj = 0, 1. The key is used both in encryption and decryption. In cryptanalysis the setup "chosen plaintext" seems to lead to an /VP-complete problem, whereas the setup "known plaintext" with a long enough plaintext leads to an easy problem.
We use the symbol © to denote bitwise addition. The notation is extended to concern vectors as well. Thus, 1©1=0 and (1, 1,0, 1,0) © (1, 1, 1, 0, 0) = (0,0,1, 1,0). Denote further
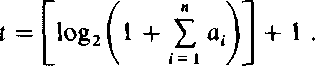
|
Clearly, any sum of the a,'s, where each individual af appears at most once, can be expressed as a binary number with t bits.
As already mentioned, A will be public, whereas the bit vector K is secret. For the encryption the plaintext is divided into blocks P = (pl5. . . ,p,) of t bits. For each P, a random bit vector R = (r,, . . . , rj is chosen. The sum
A(K®R)= £ (fc.er.Jfl,
i= 1
is formed. (Thus K © R is viewed as a column vector.) Let S be the binary representation of this sum, consisting oft bits with some initial 0's if necessary. The encrypted version of P is now
C = (L, R) where L = S 0 P ■
Thus, an (n + t)-bit cryptotext corresponds to a t-bit plaintext. Since the n last bits of the cryptotext give R, the legal recipient who knows K can immediately compute S and, therefore, the plaintext P from the t-bit initial segment L of the cryptotext.
A cryptanalyst who knows some pair (P, C), where P may even be chosen by the cryptanalyst, can immediately compute S from L®P = S@P®P = S. However, the S thus obtained corresponds to the particular plaintext P. Although R is known, the determining of K still leads to the /VP-complete knapsack problem. Therefore, the cryptanalyst has not gained much information for decrypting some other cryptotext received later.
Assume, however, that the cryptanalyst knows some pair (plaintext, cryptotext), where the plaintext is long enough. More specifically, it should consist of n t-bit blocks. This means that the cryptanalyst knows n triples (Pf, Lt, Rf), i = 1, . . . ,n.
Denote the bitwise multiplication of two n-bit vectors T and U by T* 11. Thus, the z'-th component in T* U equals 1 iff the i-th component equals 1 both in T and U. It is easily seen by induction on n that
T® U = T+ U - 2(T* V).
Indeed, for n = 1 this is obvious. Assuming the equation for two n-bit vectors, we extend it to two (n + l)-bit vectors by applying the inductive hypothesis to their last n bits (the result is an n-bit vector with no carry), after which the matter with the leading bits is the same as for n= 1. Of course, + and — above denote ordinary addition and subtraction. For instance,
Date: 2015-02-16; view: 808
| <== previous page | | | next page ==> |
| Chapter 3. Knapsack Systems 2 page | | | Chapter 3. Knapsack Systems 4 page |