
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
UNITS and DIMENSIONS NU-CPS Physics 2014-15
1.Determine the dimensions of the following quantities: speed, acceleration, volume, density.
2.Which of the following four units are equivalent?
a) kg · m2 · s-2
b) g · m · m2 · s-2
c) kg · km2 · h-2
d) kg2 · m · h-2
3.Hooke’s law states that the force, F, in a spring extended by a distance x is given by F = - kx. Starting from Newton’s second law F = ma, where m is the mass and a is the acceleration, determine the dimensions and units of the spring constant k.
4.Newton’s Law of Universal Gravitation states that two masses, m1and m2, separated by a distance r attract each other with a force F = Gm1m2/r2. What are the units of G in terms of base units? What are the dimensions of G?
5.a) What is meant by “homogeneous equation” in Physics?
b) Which of the following is always true:
i) A homogeneous equation is also valid;
ii) A valid equation is also homogeneous.
c) Verify the homogeneity of the following equations:
i) 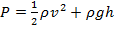 , where P is pressure, ρ is mass density, v is speed, g is gravitational acceleration, and h is height;
, where P is pressure, ρ is mass density, v is speed, g is gravitational acceleration, and h is height;
ii)  , where E is energy, m and M are masses, v is speed, and r is distance.
, where E is energy, m and M are masses, v is speed, and r is distance.
6.a) On what parameters does the period of a simple pendulum depend? b) Determine the expression of the period of a simple pendulum using dimensional analysis.
7*. Energy in a nuclear explosion
 Essentially, in a nuclear explosion there is an instantaneous release of energy in a small region of space. This produces an approximately spherical shock wave. The pressure inside the shock wave is thousands of times greater than the initial air pressure. Determine an expression for the shock wave’s radius in terms of the released energy E, time t, and the initial air density ρ0.
Essentially, in a nuclear explosion there is an instantaneous release of energy in a small region of space. This produces an approximately spherical shock wave. The pressure inside the shock wave is thousands of times greater than the initial air pressure. Determine an expression for the shock wave’s radius in terms of the released energy E, time t, and the initial air density ρ0.
[Interesting note: This problem was first addressed by the eminent British fluid dynamicist G. I. Taylor. He was able to take declassified movies of nuclear tests, and using his model, infer the yield of the bombs. These data, of course, were strictly classified; it came as a surprise to the American intelligence community that the data were, essentially, publicly available to those well versed in dimensional analysis.]
8. A cylinder has length L1 and radius of the base R1. A second cylinder has length L2 and radius R2. The following measurements are obtained:
L1 = 537.8 cm, R1 = 8.51 cm
L2 = 362.24 cm, R2 = 18.66 cm
- Calculate the volume V1 of the first cylinder. Express your answer in SI unit, in scientific notation, with the appropriate number of significant figures;
- Calculate the volume V2 of the second cylinder. Express your answer in SI unit, in scientific notation, with the appropriate number of significant figures;
- Use the answers of a) and b) to calculate the volume V1+V2 of both cylinders. Express your answer in SI unit, in scientific notation, with the appropriate number of decimal places.
PCS# 1Units and Dimensions (Answers) NU-CPS Physics 2014-15
1.Dimensions: [speed]= L T-1, [acceleration]= L T-2, [volume]= L3, [density] = M L-3 ;
2.
| units |
3.
| units |
4.[G] = M-1 L3 T-2, G = kg-1 m3 s-2 ;
5.a) [LHS]=[RHS];b) i) not always, ii) yes, always;
c)i) homogeneous; ii) not homogeneous;
7.a) T = f (m, l, g), where m is mass, l is length and g is gravitational acceleration;
b)  , where C is some real constant.
, where C is some real constant.
7*. 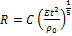 where C is some real constant.
where C is some real constant.
8. a.) 1.22 × 10-1 m3, b.) 3.963 × 10-1 m3, c) 5.18 × 10-1 m3
| Revised September 2014 |
Date: 2015-01-29; view: 1855
| <== previous page | | | next page ==> |
| PSC 38 - Faradays Law 2 with Numerical Answers | | | PSC # 2 VECTORS and SCALARS NU-CPS Physics 2014-15 |