Control de Tracción

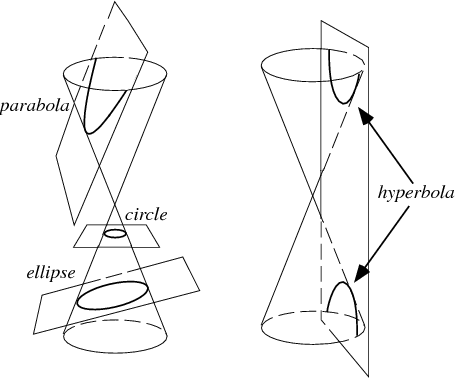
The conic sections are the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone. For a plane perpendicular to the axis of the cone, a circle is produced. For a plane that is not perpendicular to the axis and that intersects only a single nappe, the curve produced is either an ellipse or a parabola (Hilbert and Cohn-Vossen 1999, p. 8). The curve produced by a plane intersecting both nappes is a hyperbola (Hilbert and Cohn-Vossen 1999, pp. 8-9).

The ellipse and hyperbolaare known as central conics.

Because of this simple geometric interpretation, the conic sections were studied by the Greeks long before their application to inverse square law orbits was known. Apollonius wrote the classic ancient work on the subject entitled On Conics. Kepler was the first to notice that planetary orbits were ellipses, and Newton was then able to derive the shape of orbits mathematically using calculus, under the assumption that gravitational force goes as the inverse square of distance. Depending on the energy of the orbiting body, orbit shapes that are any of the four types of conic sections are possible.

A conic section may more formally be defined as the locus of a point 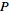that moves in the plane of a fixed point 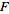called the focus and a fixed line 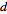called the conic section directrix (with 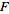not on 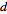) such that the ratio of the distance of 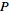from 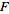to its distance from 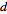is a constant 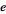called the eccentricity. If , the conic is a circle, if , the conic is an ellipse, if 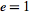, the conic is a parabola, and if 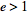, it is a hyperbola.

A conic section with conic section directrix at 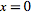, focus at 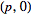, and eccentricity 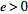has Cartesian equation

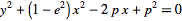
(1)

(Yates 1952, p. 36), where 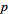is called the focal parameter. Plugging in 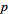gives

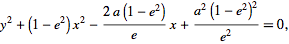
(2)

for an ellipse,

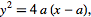
(3)

for a parabola, and

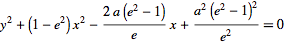
(4)

for a hyperbola.

The polar equation of a conic section with focal parameter 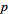is given by

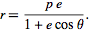
(5)

The pedal curve of a conic section with pedal point at a focus is either a circle or a line. In particular the ellipse pedal curve and hyperbola pedal curve are both circles, while the parabola pedal curve is a line (Hilbert and Cohn-Vossen 1999, pp. 25-27).

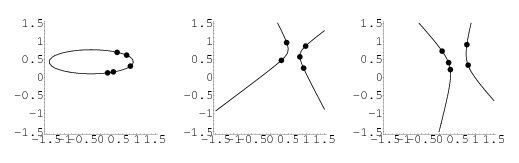
Five points in a plane determine a conic (Coxeter and Greitzer 1967, p. 76; Le Lionnais 1983, p. 56; Wells 1991), as do five tangent lines in a plane (Wells 1991). This follows from the fact that a conic section is a quadratic curve, which has general form

(6)

so dividing through by 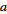to obtain

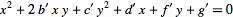
(7)

leaves five constants. Five points, for , ..., 5, therefore determine the constants uniquely. The geometric construction of a conic section from five points lying on it is called the Braikenridge-Maclaurin Construction. The explicit equation for this conic is given by the equation

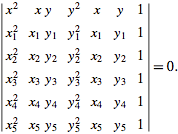
(8)

The general equation of a conic section in trilinear coordinates is

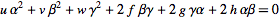
(9)

(Kimberling 1998, p. 234). For five points specified in trilinear coordinates 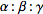, the conic section they determine is given by

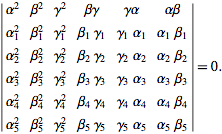
(10)

(Kimberling 1998, p. 235).

Two conics that do not coincide or have an entire straight line in common cannot meet at more than four points (Hilbert and Cohn-Vossen 1999, pp. 24 and 160). There is an infinite family of conics touching four lines. However, of the eleven regions into which plane division cuts the plane, only five can contain a conic section which is tangent to all four lines. Parabolas can occur in one region only (which also contains ellipses and one branch of hyperbolas), and the only closed region contains only ellipses.

Let a polygon of 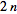sides be inscribed in a given conic, with the sides of the polygon being termed alternately "odd" and "even" according to some definite convention. Then the 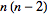points where an odd side meet a nonadjacent even side lie on a curve of order 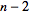(Evelyn et al. 1974, p. 30).

Control de Tracción

Fecha: 1986

Utilidad: Evitar el deslizamiento de las ruedas motrices de un vehículo en el momento de acelerar.

Inventor: Bosch

El control de tracción es un sistema de seguridad automovilística lanzado al mercado por Bosch en 1986 y diseñado para prevenir la pérdida de adherencia de las ruedas y que éstas patinen cuando el conductor se excede en la aceleración del vehículo o el firme está muy deslizante (ej.: hielo). En general se trata de sistemas electrohidráulicos.

Funciona de tal manera que, mediante el uso de los mismos sensores y accionamientos que emplea el sistema ABS, antibloqueo de frenos, se controla si en la aceleración una de las ruedas del eje motor del automóvil patina, es decir, gira a mayor velocidad de la que debería, y, en tal caso, el sistema actúa con el fin de reducir el par de giro y así recuperar la adherencia entre neumático y firme, realizando una (o más de una a la vez) de las siguientes acciones:

Retardar o suprimir la chispa a uno o más cilindros.

Reducir la inyección de combustible a uno o más cilindros.

Frenar la rueda que ha perdido adherencia.

Algunas situaciones comunes en las que puede llegar a actuar este sistema son las aceleraciones bruscas sobre firmes mojados y/o con grava, así como sobre caminos de tierra y en superficie helada.

Las siglas más comunes para denominar este sistema son ASR (o Anti-Slip Regulation) y TCS (Traction Control System)

Date: 2014-12-22; view: 1317