HT-rock deformation

-----

Plastic deformation and dislocations. Stress vs stain-rate behaviour ; experimental deformation and flow laws. Defects in crystals. Dislocations : edge, screw and dislocation loops. Slip systems. Role of stress; role of temperature ; dislocation creep. Strain localization. Shape and lattice preferred orientations (SPO / LPO) : LPO diagrams of quartz.

At « high » temperature, rocks behave in a ductile fashion, i.e. plastically.

Two principal mechanims are responsible for plastic deformation : 1) Intracrystalline plasticity, and 2) Pressure solution. In the first one, deformation is achieved through the mobility of dislocations. In the second one, deformation is achieved through dissolution, transport and precipitation. The first one is rather a MT to HT mechanism ; the second one is rather a low-T one and needs the presence of a solvent (fluid, usually water). The first one is a rapid (quick) mechanism and necessitates rather high (differential) stress ; the second is a slow mechanism which may work even at very low stress.

I. Intracrystalline plasticity

1. Macroscopic description

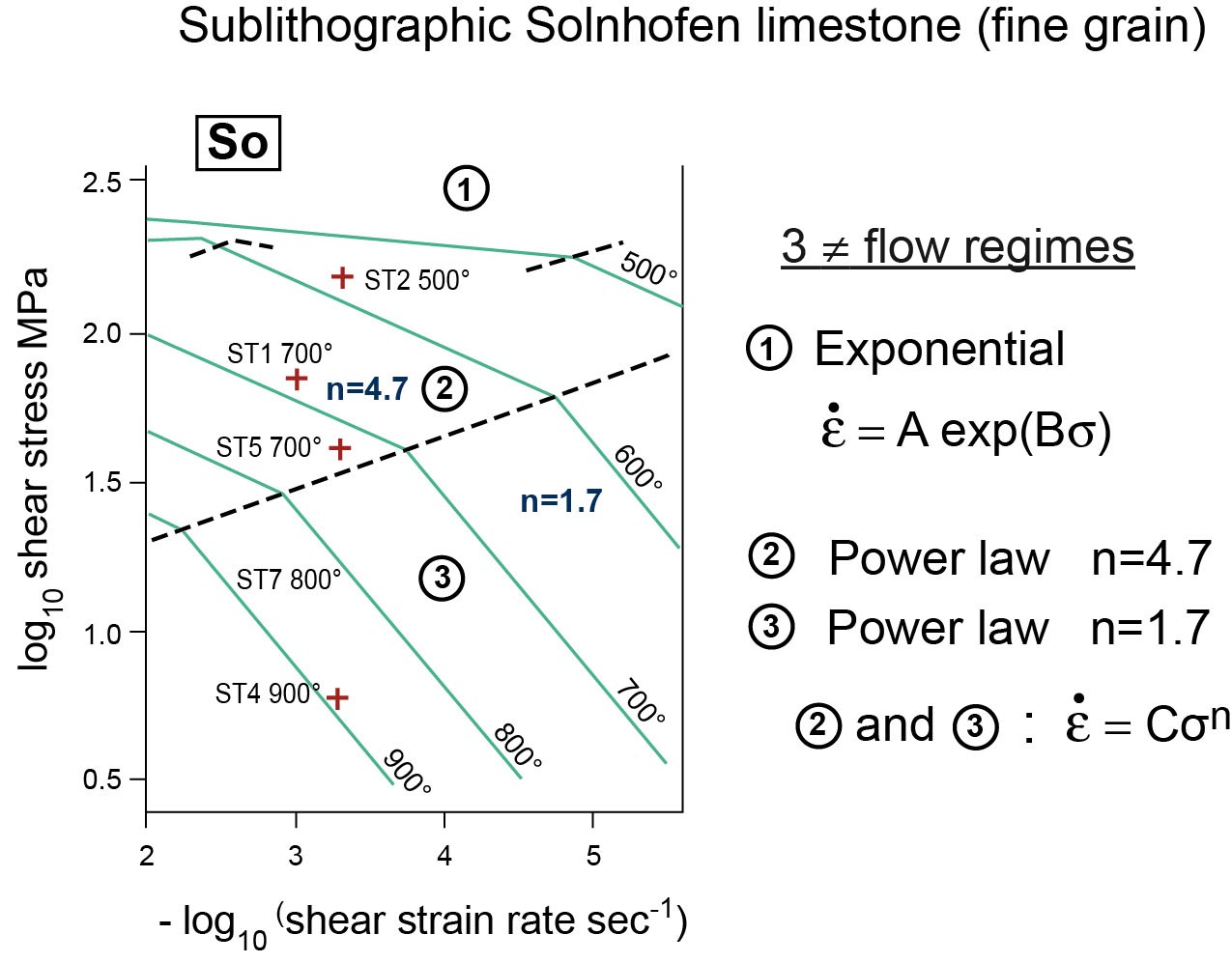
Re-examine a stress-strain relationship and a strain-rate behaviour (Figures : quartz and calcite, deformed by intracrystalline plasticity)

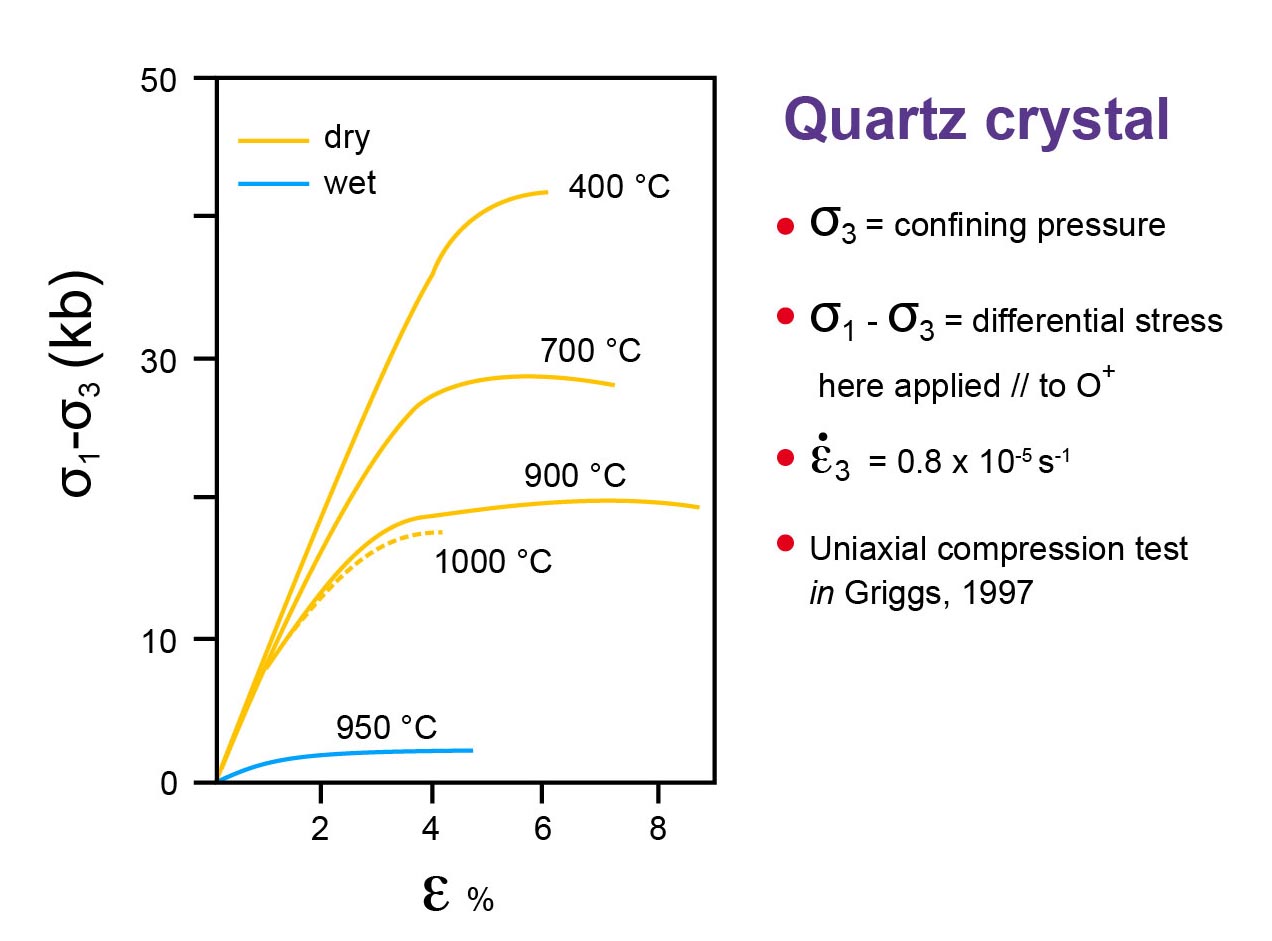
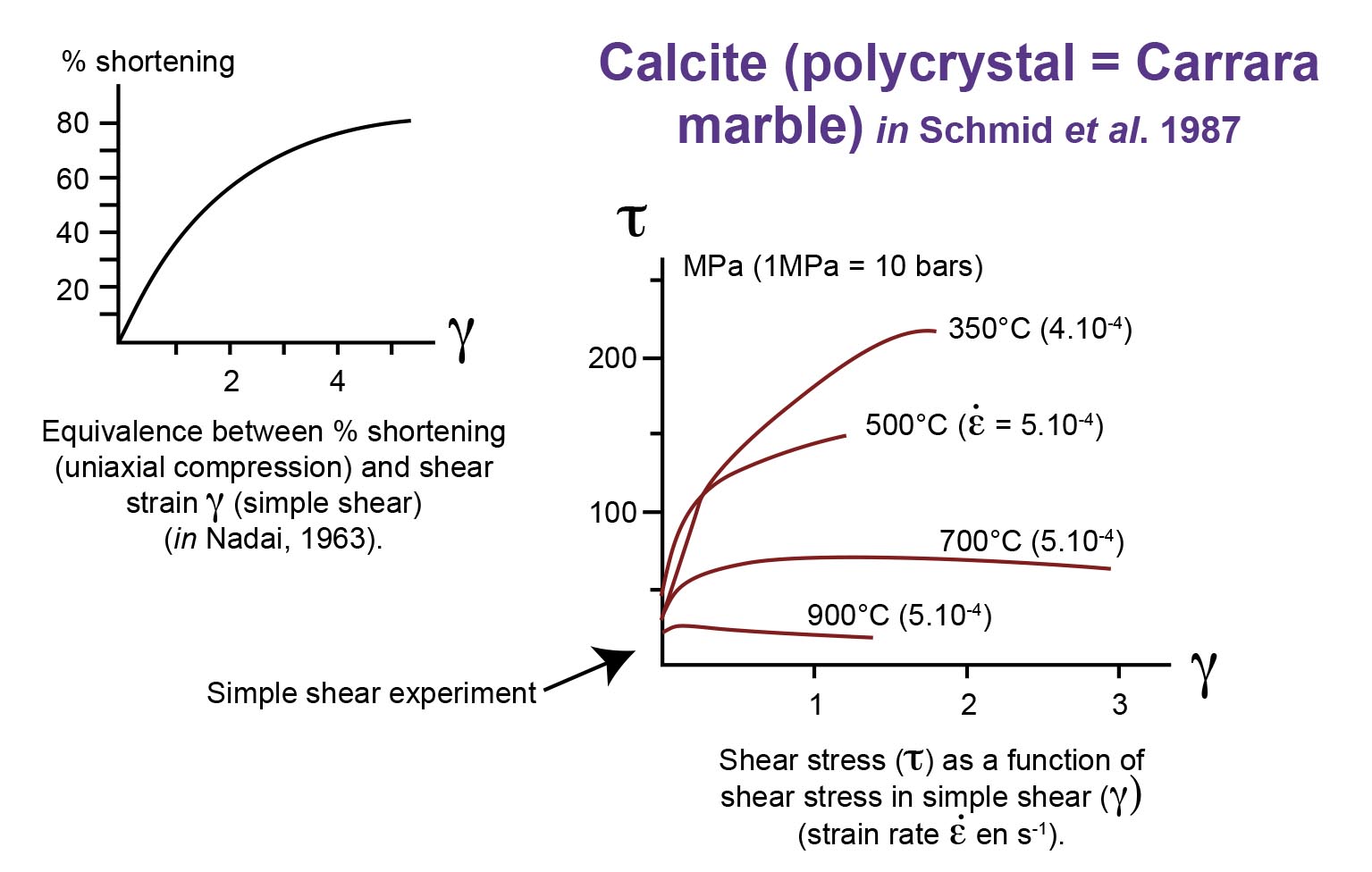
- Have a look at the HT/HP experimental deformation device (Griggs’ apparatus ; Figure)

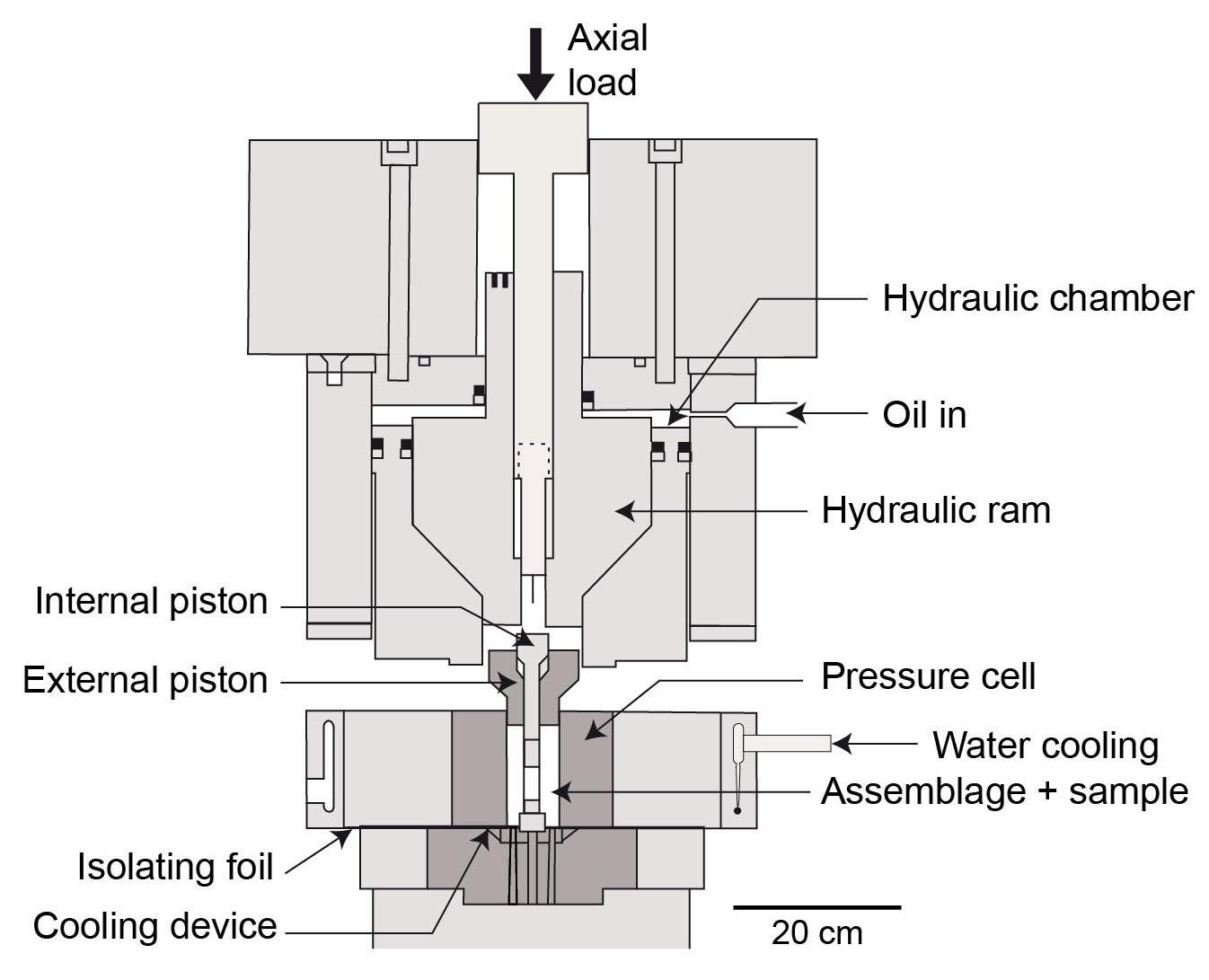
Figure : Griggs’ apparatus : the confining pressure in the specimen assemblage is realized either using gaz (Argon) or, more usually, talc or halite (salt).

As already mentionned, by simply using s versus e diagrams (see the above diagrams), the viscosity (h) of the material (i.e. its resistance to deformation : F/S = h v/l (of viscosimetres) or s = h e’) cannot be taken into account.

This is why, s versus e’ = de/dt (strain rate, in s^-1) diagrams are used to describe the macroscopic behaviours of plastic materials.

Flow laws of materials are therefore represented through (e’, s, T) relationships, usually under the following form :

e’ = K sⁿ D (T) (power flow laws)

where n is called the stress exponent (usually in-between 1 and 3) and D, the diffusion term (which is very dependent on temperature : D = exp (-Q/RT)).

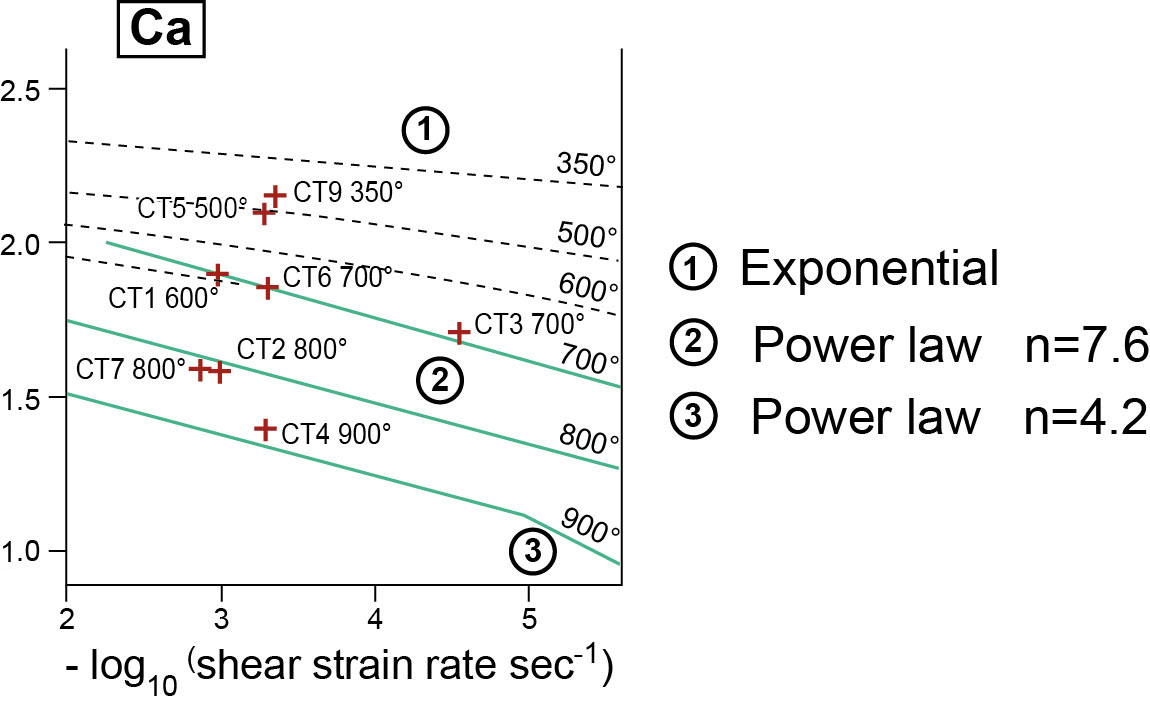
Discuss the rôle of n :

n = 1 Newtonian behaviour : non localizing behaviour

n = 3 dislocation creep : localizing behaviour

Carrara marble

Date: 2015-01-29; view: 2624