
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Differential equations
I. Scan the article to find out:
- who was the pioneer in differential equations
- what was the harder part of the theory of differential equations
- what William Rowan Hamilton in Ireland and Jacobi in Germany showed
Another field that developed considerably in the 19th century was the theory of differential equations. The pioneer in this direction once again was Cauchy. Above all, he insisted that one should prove that solutions do indeed exist; it is not a priori obvious that every ordinary differential equation has solutions. The methods that Cauchy proposed for these problems fitted naturally into his program of providing rigorous foundations for all the calculus. The solution method he preferred, although the less general of his two approaches, worked equally well in the real and complex cases. It established the existence of a solution equal to the one obtainable by traditional power series methods using newly developed techniques in his theory of functions of a complex variable.
The harder part of the theory of differential equations concerns partial differential equations, those for which the unknown function is a function of several variables. In the early 19th century there was no known method of proving that a given second- or higher-order partial differential equation had a solution, and there was not even a method of writing down a plausible candidate. In this case progress was to be much less marked. Cauchy found new and more rigorous methods for first-order partial differential equations, but the general case eluded treatment.
An important special case was successfully prosecuted, that of dynamics. Dynamics is the study of the motion of a physical system under the action of forces. Working independently of each other, William Rowan Hamilton in Ireland and Jacobi in Germany showed how problems in dynamics could be reduced to systems of first-order partial differential equations. From this base grew an extensive study of certain partial differential operators. These are straightforward generalizations of a single partial differentiation (∂/∂x) to a sum of the form
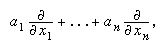
where the a's are functions of the x's. The effect of performing several of these in succession can be complicated, but Jacobi and the other pioneers in this field found that there are formal rules which such operators tend to satisfy. This enabled them to shift attention to these formal rules, and gradually an algebraic analysis of this branch of mathematics began to emerge.
The most influential worker in this direction was the Norwegian, Sophus Lie. Lie, and independently Wilhelm Killing in Germany, came to suspect that the systems of partial differential operators they were studying came in a limited variety of types. Once the number of independent variables was specified (which fixed the dimension of the system), a large class of examples, including many of considerable geometric significance, seemed to fall into a small number of patterns. This suggested that the systems could be classified, and such a prospect naturally excited mathematicians. After much work by Lie and Killing and later by the French mathematician Élie-Joseph Cartan, they were classified. Initially, this discovery aroused interest because it produced order where previously the complexity had threatened chaos and because it could be made to make sense geometrically. The realization that there were to be major implications of this work for the study of physics lay well in the future.
II. Translate the attributive groups in the sentences:
1.…method of proving that a given second- or higher-order partial differential equation had a solution…
2. Cauchy found new and more rigorous methods for first-order partial differential equations
III. Read the article in details and answer the questions:
1.Does every ordinary differential equation have solutions?
2. What methods did Cauchy propose for these problems?
3. What did his solution method establish?
4. What was the harder part of the theory of differential equations?
5. Why was it hard?
6. What was Cauchy's contribution to it?
7. What special case was successfully prosecuted?
8. What did William Rowan Hamilton in Ireland and Jacobi in Germany show?
9. What was their contribution to the study of partial differential equations?
10. What did Sophus Lie and Wilhelm Killing realise?
11. What did this suggest?
12. Why did this discovery arouse interest?
Cantor
Before you read: Have you heard about Cantor? What do you know about him? What is he famous for?
Look through the article quickly. What other names are mentioned in it ? Why do you think they are mentioned? What are your predictons?
1. All of these debates came together through the pioneering work of the German mathematician Georg Cantor on the concept of a set. Cantor had begun work in this area because of his interest in Riemann's theory of trigonometric series, but the problem of what characterized the set of all real numbers came to occupy him more and more. He began to discover unexpected properties of sets. For example, he could show that the set of all algebraic numbers, and a fortiori the set of all rational numbers, is countable in the sense that there is a one-to-one correspondence between the integers and the members of each of these sets by means of which for any member of the set of algebraic numbers (or rationals), no matter how large, there is always a unique integer it may be placed in correspondence with. But, more surprisingly, he could also show that the set of all real numbers is not countable. So, although the set of all integers and the set of all real numbers are both infinite, the set of all real numbers is a strictly larger infinity. This was in complete contrast to the prevailing orthodoxy, which proclaimed that infinite could only mean “larger than any finite amount.”
2. Here the concept of number was being extended and undermined at the same time. The concept was extended because it was now possible to count and order sets that the set of integers was too small to measure; and it was undermined because even the integers ceased to be basic undefined objects. Cantor himself had given a way of defining real numbers as certain infinite sets of rational numbers. Rational numbers were easy to define in terms of the integers, but now integers could be defined by means of sets. One way was given by Frege in Die Grundlagen der Arithmetik (1884). He regarded two sets as the same if they contained the same elements. So in his opinion there was only one empty set (today symbolized by Ø), the set with no members. A second set could be defined as having only one element by letting that element be the empty set itself (symbolized by {Ø}), a set with two elements by letting them be the two sets just defined (i.e., {Ø, {Ø}}), and so on. Having thus defined the integers in terms of the primitive concepts “set” and “element of,” Frege agreed with Cantor that there was no logical reason to stop, and he went on to define infinite sets in the same way Cantor had. Indeed, Frege was clearer than Cantor about what sets and their elements actually were.
3. Frege's proposals went in the direction of a reduction of all mathematics to logic. He hoped that every mathematical term could be defined precisely and manipulated according to agreed, logical rules of inference. This, the “logicist” program, was dealt an unexpected blow by the English mathematician and philosopher Bertrand Russell in 1902, who pointed out unexpected complications with the naive concept of a set. Nothing seemed to preclude the possibility that some sets were elements of themselves while others were not, but asked Russell, “what then of the set of all sets that were not elements of themselves?” If it is an element of itself, then it is not (an element of itself), but, if it is not, then it is—a paradox. Either the idea of a set as an arbitrary collection of already defined objects was flawed, or else the idea that one could legitimately form the set of all sets of a given kind was incorrect. Frege's program never recovered from this blow, and the theories of Russell, which he developed together with Alfred North Whitehead in their Principia Mathematica (1910–13), that went in the same direction never found lasting appeal with mathematicians.
4. Greater interest attached to the ideas that Hilbert and his school began to advance. It seemed to them that what had worked once for geometry could work again for all of mathematics. Rather than attempt to define things so that problems could not arise, they suggested that it was possible to dispense with definitions and cast all of mathematics in an axiomatic structure using the ideas of set theory. Indeed, the hope was that the study of logic could be embraced in this spirit, thus making logic a branch of mathematics, the opposite of Frege's intention. There was considerable progress in this direction, and there emerged both a powerful school of mathematical logicians (notably in Poland) and an axiomatic theory of sets that avoided Russell's paradoxes and the others which had sprung up.
5. In the 1920s Hilbert put forward his most detailed proposal for establishing the validity of mathematics. According to his theory of proofs, everything was to be put into an axiomatic form, allowing the rules of inference to be only those of elementary logic, and only those conclusions that could be reached from this finite set of axioms and rules of inference were to be admitted. He proposed that a satisfactory system would be one which was consistent, complete, and decidable. By consistent Hilbert meant that it should be impossible to derive both a statement and its negation; by complete, that every properly written statement should be such that either it or its negation was derivable from the axioms; by decidable, that one should have an algorithm which determines of any given statement whether it or its negation is provable. Such systems did exist, for example, the first-order predicate calculus, but none had been found capable of allowing mathematicians to do interesting mathematics.
6. Hilbert's program, however, did not last long. In 1931 the Austrian-born American mathematician and logician Kurt Gödel showed that there was no system of Hilbert's type within which the integers could be defined and which was both consistent and complete. Later Gödel and, independently, the English mathematician Alan Turing showed that decidability was also unattainable. Perhaps paradoxically, the effect of this dramatic discovery was to alienate mathematicians from the whole debate. Instead, mathematicians, who may not have been too unhappy with the idea that there is no way of deciding the truth of a proposition automatically, learned to live with the idea that not even mathematics rests on rigorous foundations. Progress since has been in other directions. An alternative axiom system for set theory was later put forward by the Hungarian-born American mathematician John von Neumann, which he hoped would help resolve contemporary problems in quantum mechanics. There was also a renewal of interest in statements that are both interesting mathematically and independent of the axiom system in use. The first of these was the American mathematician Paul Cohen's surprising resolution in 1963 of the continuum hypothesis, which was Cantor's conjecture that the set of all subsets of the rational numbers was of the same size as the set of all real numbers. This turns out to be independent of the usual axioms for set theory, so there are set theories (and therefore types of mathematics) in which it is true and others in which it is false.
I. Look up the words and word combinations in the Russian – English dictionary and learn them:
trigonometric series, a fortiori, a one-to-one correspondence, an infinite set, a rational number, an empty set, a reduction of mathematics to logic, a mathematical term, a logical rule of inference, problems arise, to cast mathematics in an axiomatic structure, set theory, an axiomatic theory of sets, the theory of proofs, rules of inference, to reach a conclusion, a finite set of axioms, first-order predicate calculus, quantum mechanics, the continuum hypothesis.
II. Write out from the passage and learn all the possible word combinations with the word "set".
III. In what meaning are the italicized words used in the article? Translate the sentences into Russian.
1.…but the problem of what characterized the set of all real numbers came to occupy him more and more.
2. He hoped that every mathematical term could be defined precisely and manipulated according to agreed, logical rules of inference.
3. This, the “logicist” program, was dealt an unexpected blow…
4. It seemed to them that what had worked once for geometry could work again for all of mathematics.
5. So, although the set of all integers and the set of all real numbers are both infinite, the set of all real numbers is a strictly larger infinity
6. Perhaps paradoxically, the effect of this dramatic discovery was to alienate mathematicians from the whole debate.
IV. What do the pronouns "it" and "one" in the sentences stand for? Study the context and translate the sentences into Russian.
1. If it is an element of itself, then it is not (an element of itself), but, if it is not, then it is—a paradox.
2.…or else the idea that one could legitimately form the set of all sets of a given kind was incorrect.
3. He proposed that a satisfactory system would be one which was consistent, complete, and decidable.
4. … by decidable, that one should have an algorithm which determines of any given statement whether it or its negation is provable.
V. Suggest the right translation of the Non-Finite Forms of the verbs in the sentences:
1. Frege agreed with Cantor that there was no logical reason to stop, and he went on to define infinite sets in the same way Cantor had
2…it was now possible to count and order sets that the set of integers was too small to measure.
3. Cantor himself had given a way of defining real numbers as certain infinite sets of rational numbers.
4. A second set could be defined as having only one element by letting that element be the empty set itself (symbolized by {Ø}), a set with two elements by letting them be the two sets just defined (i.e., {Ø, {Ø}}), and so on.
5….the hope was that the study of logic could be embraced in this spirit, thus making logic a branch of mathematics, the opposite of Frege's intention.
6. In the 1920s Hilbert put forward his most detailed proposal for establishing the validity of mathematics.
7….but none had been found capable of allowing mathematicians to do interesting mathematics.
8…. mathematicians, who may not have been too unhappy with the idea that there is no way of deciding the truth of a proposition automatically…
VI. How will you translate the ellipsis in the sentence?
…there is a one-to-one correspondence between the integers and the members of each of these sets by means of which for any member of the set of algebraic numbers (or rationals), no matter how large, there is always a unique integer it may be placed in correspondence with
VII. How will you show the emphasis in translating the sentences:
1…but asked Russell, “what then of the set of all sets that were not elements of themselves?”
2. Such systems did exist…
3. Progress since has been in other directions.
VIII. Read the article again and match the statements with the paragraphs:
a) Frege was clearer than Cantor about what sets and their elements actually were
b) the ideas that Hilbert and his school began to advance attracted greater interest
c) Bertrand Russell pointed out unexpected complications with the naive concept of a set.
d) the pioneering work of Georg Cantor on the concept of a set
e) an alternative axiom system for set theory was later put forward by John von Neumann
f) Hilbert proposed consistency, completeness, and decidability for a satisfactory system
IX. Read the article and fill in the table with information about the contribution of each of the writers to the theory of sets
| Cantor | Frege | Russell | Hilbert | Gödel and Turing |
Date: 2015-01-29; view: 1097
| <== previous page | | | next page ==> |
| Riemann | | | Mathematical physics |