Mathematics in the 10th century

Islāmic scientists in the 10th century were involved in three major mathematical projects: the completion of arithmetic algorithms, the development of algebra, and the extension of geometry.

The first of these projects led to the appearance of three complete numeration systems, one of which was the finger arithmetic used by the scribes and treasury officials. This ancient arithmetic system, which became known throughout the East and Europe, employed mental arithmetic and a system of storing intermediate results on the fingers as an aid to memory. (Its use of unit fractions recalls the Egyptian system.) During the 10th and 11th centuries capable mathematicians, such as Abū al-Wafāʾ (940–997/8), wrote on this system, but it was eventually replaced by the decimal system.

A second common system was the base-60 numeration inherited from the Babylonians via the Greeks and known as the arithmetic of the astronomers. Although astronomers used this system for their tables, they usually converted numbers to the decimal system for complicated calculations and then converted the answer back to sexagesimals.

The third system was Indian arithmetic, whose basic numeral forms, complete with the zero, eastern Islām took over from the Hindus. (Different forms of the numerals, whose origins are not entirely clear, were used in the western part of Islām.) The basic algorithms also came from India, but these were adapted by al-Uqlīdisī (c. 950) to pen and paper instead of the traditional dust board, a move that helped to popularize this system. Also, the arithmetic algorithms were completed in two ways: by the extension of root-extraction procedures, known to Hindus and Greeks only for square and cube roots, to roots of higher degree, and by the extension of the Hindu decimal system for whole numbers to include decimal fractions. These fractions appear simply as computational devices in the work of both al-Uqlīdisī and al-Baghdādī (c. 1000), but in subsequent centuries they received systematic treatment as a general method. As for extraction of roots, Abū al-Wafāʿ wrote a treatise (now lost) on the topic, and Omar Khayyam (ʾUmar al-Khayyāmī [1048–1131]) solved the general problem of extracting roots of any desired degree. Omar's treatise, too, is lost, but the method is known from other writers, and it appears that a major step in its development was al-Karajī's 10th-century derivation by means of mathematical induction of the binomial theorem for whole-number exponents—i.e., his discovery that

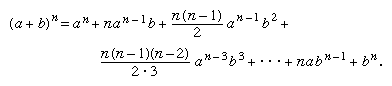
During the 10th century Islāmic algebraists progressed from al-Khwārizmī's quadratic polynomials to the mastery of the algebra of expressions involving arbitrary positive or negative integral powers of the unknown. Several algebraists explicitly stressed the analogy between the rules for working with powers of the unknown in algebra and those for working with powers of 10 in arithmetic, and there was interaction between the development of arithmetic and algebra from the 10th to the 12th century. A 12th-century student of al-Karajī's works, as-Samawʿal, was able to approximate the quotient (20x² + 30x)/(6x² + 12) as

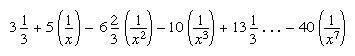
and also gave a rule for finding the coefficients of the successive powers of 1/x. Although none of this employed symbolic algebra, algebraic symbolism was in use by the 14th century in the western part of the Islāmic world. The context for this well-developed symbolism was, it seems, commentaries that were destined for teaching purposes, such as that of Ibn Qunfūdh (1330–1407) of Algeria on the algebra of Ibn al-Bannāʿ (1256–1321) of Morocco.

Other parts of algebra developed as well. Both Greeks and Hindus had studied indeterminate equations, and the translation of this material and the application of the newly developed algebra led to the investigation of Diophantine equations by writers like Abū Kāmil, al-Karajī, and Abū Jaʿfar al-Khāzin (first half of 10th century), as well as to attempts to prove a special case of what is now known as Fermat's last theorem, namely that there are no rational solutions to x³ + y³ = z³. The great scientist Alhazen (Ibn al-Haytham [965–1041]) solved problems involving congruences by what is now called Wilson's theorem, which states that, if p is a prime, then p divides (p - 1) × (p − 2) . . . × 2 × 1 + 1, and al-Baghdādī gave a variant of the idea of amicable numbers by defining two numbers to “balance” if the sums of their divisors are equal.

However, not only arithmetic and algebra but geometry too underwent extensive development. Thābit ibn Qurrah, his grandson Ibrāhīm ibn Sinān (909–946), Abū Sahl al-Kūhī (d. c. 995), and Alhazen solved problems involving the pure geometry of conic sections, including the areas and volumes of plane and solid figures formed from them, and also investigated the optical properties of mirrors made from conic sections. Ibrāhīm ibn Sinān, Abu Sahl al-Kūhī, and Alhazen used the ancient technique of analysis to reduce the solution of problems to constructions involving conic sections. (Alhazen, for example, used this method to find the point on a convex spherical mirror at which a given object is seen by a given observer.) Thābit and Ibrāhīm showed how to design the curves needed for sundials. Abū al-Wafāʾ, whose book on the arithmetic of the scribes is mentioned above, also wrote on geometric methods needed by artisans.

In addition, in the late 10th century Abū al-Wafāʿ and the prince Abū Naṣr Manṣur stated and proved theorems of plane and spherical geometry that could be applied by astronomers and geographers, including the laws of sines and tangents. Abū Naṣr's pupil al-Bīrūnī (973–1050), who produced a vast amount of high-quality work, was one of the masters in applying these theorems to astronomy and to such problems in mathematical geography as the determination of latitudes and longitudes, the distances between cities, and the direction from one city to another.

I. Read the passage and say how it is structured. Find the main logical parts that the passage is divided into. How are these parts made clear to the readers? What formal elements are these parts introduced by?

II. Suggest the Russian counterparts for the following words and expressions:

a numeration system, finger arithmetic, mental arithmetic, a unit fraction, the base-60 numeration, to convert to, a basic algorithm, the root-extraction procedure, square and cube roots, decimal fractions, to write a treatise, by means of, mathematical induction, the binomial theorem, a whole-number exponent, a Diophantine equation, a quadratic polynomial, an integral power, to give a rule for, symbolic algebra, indeterminate equations, to lead to, to solve a problem, to undergo development, the pure geometry of conic sections, volumes of solid figures, the optical properties of mirrors, to reduce to, a convex spherical mirror, the laws of sines and tangents, the determination of latitudes and longitudes.

III. In what meaning are the italicized words and phrases used in the sentences? Suggest the way of their translation into Russian.

1.…these were adapted by al-Uqlīdisī (c. 950) to pen and paper instead of the traditional dust board..

2.… the arithmetic algorithms were completed in two ways…

3. A 12th-century student of al-Karajī's works..

4. Abū Naṣr's pupil al-Bīrūnī (973–1050), who produced a vast amount of high-quality work…

5. …complete with the zero

6. … were used in the western part of Islām

IV. How do you understand the following sentences:

1. Also, the arithmetic algorithms were completed in two ways: by the extension of root-extraction procedures, known to Hindus and Greeks only for square and cube roots, to roots of higher degree, and by the extension of the Hindu decimal system for whole numbers to include decimal fractions.

2.…and it appears that a major step in its development was al-Karajī's 10th-century derivation by means of mathematical induction of the binomial theorem for whole-number exponents

3…. al-Baghdādī gave a variant of the idea of amicable numbers by defining two numbers to “balance” if the sums of their divisors are equal.

4. …the areas and volumes of plane and solid figures formed from them

5. …and Alhazen used the ancient technique of analysis to reduce the solution of problems to constructions involving conic sections.

V. Read the passage again and present its summary.

European mathematics during the Middle Ages and Renaissance

Until the 11th century only a small part of the Greek mathematical corpus was known in the West. Because almost no one could read Greek, what little was available came from the poor texts written in Latin in the Roman Empire, together with the very few Latin translations of Greek works. Of these the most important were the treatises by Boethius, who in about AD 500 made Latin redactions of a number of Greek scientific and logical writings. His Arithmetic, which was based on Nicomachus, was well known and was the means by which medieval scholars learned of Pythagorean number theory. Boethius and Cassiodorus provided the material for the part of the monastic education called the quadrivium: arithmetic, geometry, astronomy, and music theory. Together with the trivium (grammar, logic, rhetoric), these subjects formed the seven liberal arts, which were taught in the monasteries, cathedral schools, and, from the 12th century on, in the universities and which constituted the principal university instruction until modern times.

For monastic life it sufficed to know how to calculate with Roman numerals. The principal application of arithmetic was a method for determining the date of Easter, the computus, that was based on the lunar cycle of 19 solar years (i.e., 235 lunar revolutions) and the 28-year solar cycle. Between the time of Bede (d. 735), when the system was fully developed, and about 1500, the computus was reduced to a series of verses that were learned by rote. Until the 12th century, geometry was largely concerned with approximate formulas for measuring areas and volumes in the tradition of the Roman surveyors. About AD 1000 the French scholar Gerbert of Aurillac, later Pope Sylvester II, introduced a type of abacus, in which numbers were represented by stones bearing Arabic numerals. Such novelties were known to very few.

Date: 2015-01-29; view: 1426