
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The numeral system and arithmetic operations
Unlike the Egyptians, the mathematicians of the Old Babylonian period went far beyond the immediate challenges of their official accounting duties; for example, they introduced a versatile numeral system, which, like the modern system, exploited the notion of place value, and they developed computational methods that took advantage of this means of expressing numbers; they solved linear and quadratic problems by methods much like those now used in school algebra; their success with the study of what are now called Pythagorean number triples was a remarkable feat in number theory. The scribes who made such discoveries must have believed mathematics to be worthy of study in its own right, not just as a practical tool.
The older Sumerian system of numerals followed an additive decimal (base-10) principle similar to that of the Egyptians. But the Old Babylonian system converted this into a place-value system with the base of 60 (sexagesimal). The reasons for the choice of 60 are obscure, but one good mathematical reason might have been the existence of so many divisors (2, 3, 4, and 5, and some multiples) of the base, which would have greatly facilitated the operation of division. For numbers from 1 to 59, the symbols for 1 and for 10 * were combined in the simple additive manner (e.g., represented 32). But, to express larger values, the Babylonians applied the concept of place value: for example, 60 was written as , 70 as , 80 as , and so on. In fact, could represent any power of 60. The context determined which power was intended. The Babylonians appear to have developed a placeholder symbol that functioned as a zero by the 3rd century BC, but its precise meaning and use is still uncertain. Furthermore, they had no mark to separate numbers into integral and fractional parts (as with the modern decimal point). Thus, the three-place numeral 3 7 30 could represent 3 1/8 (i.e., 3 + 7/60 + 30/602), 187 1/2 (i.e., 3 × 60 + 7 + 30/60), 11,250 (i.e., 3 × 602 + 7 × 60 + 30), or a multiple of these numbers by any power of 60.
The four arithmetic operations were performed in the same way as in the modern decimal system, except that carrying occurred whenever a sum reached 60 rather than 10. Multiplication was facilitated by means of tables; one typical tablet lists the multiples of a number by 1, 2, 3, . . . , 19, 20, 30, 40, and 50. To multiply two numbers several places long, the scribe first broke the problem down into several multiplications, each by a one-place number, and then looked up the value of each product in the appropriate tables. He found the answer to the problem by adding up these intermediate results. These tables also assisted in division, for the values that head them were all reciprocals of regular numbers.
Regular numbers are those whose prime factors divide the base; the reciprocals of such numbers thus have only a finite number of places (by contrast, the reciprocals of nonregular numbers produce an infinitely repeating numeral). In base 10, for example, only numbers with factors of 2 and 5 (e.g., 8 or 50) are regular, and the reciprocals ( 1/8 = 0.125, 1/50 = 0.02) have finite expressions; but the reciprocals of other numbers (such as 3 and 7) repeat infinitely 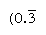 and
and 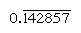 , respectively, where the bar indicates the digits that continually repeat). In base 60, only numbers with factors of 2, 3, and 5 are regular; for example, 6 and 54 are regular, so that their reciprocals (10 and 1 6 40) are finite. The entries in the multiplication table for 1 6 40 are thus simultaneously multiples of its reciprocal 1/54. To divide a number by any regular number, then, one can consult the table of multiples for its reciprocal.
, respectively, where the bar indicates the digits that continually repeat). In base 60, only numbers with factors of 2, 3, and 5 are regular; for example, 6 and 54 are regular, so that their reciprocals (10 and 1 6 40) are finite. The entries in the multiplication table for 1 6 40 are thus simultaneously multiples of its reciprocal 1/54. To divide a number by any regular number, then, one can consult the table of multiples for its reciprocal.
An interesting tablet in the collection of Yale University (see photograph) shows a square with its diagonals; on one side is written “30,” under one diagonal “42 25 35,” and right along the same diagonal “1 24 51 10” (i.e., 1 + 24/60 + 51/602 + 10/603). This third number is the correct value of √2 to four sexagesimal places (equivalent in the decimal system to 1.414213 . . . , which is too low by only 1 in the seventh place), while the second number is the product of the third number and the first and so gives the length of the diagonal when the side is 30. The scribe thus appears to have known an equivalent of the familiar long method of finding square roots. An additional element of sophistication is that, by choosing 30 (that is, 1/2) for the side, the scribe obtained as the diagonal the reciprocal of the value of √2 (since √2/2 = 1/√2), a result useful for purposes of division.
*Note: 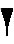 - stands for 1,
- stands for 1, 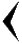 - stands for 10
- stands for 10
I. Using the symbols fill in the gaps in paragraph 2
II. Look up the following words and phrases in the dictionary and suggest their Russian counterparts. Then read the passage and find out what other words must be looked up in the dictionary. Classify all the words into three groups: mathematical terms, general scientific words and words of General English. Decide which of them need your greater concentration.
a numeral system , place value, to develop computational methods, to take advantage of, to solve linear and quadratic problems, Pythagorean number triples, a number theory, to be worthy of, in one's own right, a practical tool, reasons for, similar to, a divisor, a multiple, the operation of division, e.g. = for example, in fact, a placeholder symbol, furthermore, integral and fractional parts, the decimal point, to perform arithmetic operations, in the same way, the multiple of a number, to multiply numbers, the product, a reciprocal, regular numbers, a prime factor, by contrast, an infinitely repeating numeral, respectively, the multiplication table, equivalent to, to find square roots, a square with its diagonals, i.e. = that is, element of sophistication
III. Suggest synonyms for the following words from the passage:
Exploit, notion, value, infinitely
IV. What is the meaning of "that ", "this" and "those" in the sentences? Translate them into Russian.
1. The older Sumerian system of numerals followed an additive decimal (base-10) principle similar to that of the Egyptians.
2. But the Old Babylonian system converted this into a place-value system with the base of 60 (sexagesimal).
3. Regular numbers are those whose prime factors divide the base; the reciprocals of such numbers thus have only a finite number of places (by contrast, the reciprocals of nonregular numbers produce an infinitely repeating numeral).
V. Translate the sentences and phrases from the passage paying special attention to the use of the Passive Voice:
1.…their success with the study of what are now called Pythagorean number triples was a remarkable feat in number theory.
2. For numbers from 1 to 59, the symbols for 1 and for 10 were combined in the simple additive manner
3.…for example, 60 was written as ,
4. The context determined which power was intended.
5. The four arithmetic operations were performed in the same way as in the modern decimal system,…
6. Multiplication was facilitated by means of tables.
7.…on one side is written “30,”…
VI. Suggest the correct translation of the Subjective Infinitive Construction in the sentences:
1. The Babylonians appear to have developed a placeholder symbol…
2. The scribe thus appears to have known an equivalent of the familiar long method of finding square roots.
VII. Analyse the meaning and form of the modal verbs in the sentences and translate them into Russian:
1. The scribes who made such discoveries must have believed mathematics to be worthy of study in its own right, not just as a practical tool.
2.…one good mathematical reason might have been the existence of so many divisors.
3. In fact, could represent any power of 60.
4. To divide a number by any regular number, one can consult the table of multiples for its reciprocal.
VIII. Translate the passage into Russian taking into account the previous tasks.
Date: 2015-01-29; view: 4415
| <== previous page | | | next page ==> |
| From the history of mathematics | | | The numeral system and arithmetic operations |