Caricatures

Pupils of the Middle Ages considered the proof of Pythagorean theorem very difficult and called it Dons asinorum-the asinine bridge, or elefuga-flight "poor" as some "poor" pupils who didn't have serious mathematical preparation ran from geometry. The bad pupils who learned theorems by heart, without understanding, and nicknamed therefore "donkeys", weren't able to overcome Pythagorean theorem serving for them like the insuperable bridge. Because of the drawings accompanying Pythagorean theorem, pupils called it also "windmill", constituted verses it seems "Pythagorean trousers on all parties are equal", drew caricatures.

opening of the theorem. Tell that in honor of this opening Pythagoras sacrificed 100 bulls.

The theorem of Pythagoras-one from main and, it is possible to tell, the most important theorem of geometry. Its value consists that or with its help it is possible to remove the majority of theorems of geometry from it. Pythagorean theorem is remarkable also that in itself it isn't obvious at all. For example, it is possible to see properties of an isosceles triangle directly on the drawing. But how many look at a rectangular triangle, you won't see in any way that between its parties there is a simple ratio: c2=a2 +b2.

Upward

ProofNo. 1 (elementary)

The square constructed on a hypotenuse of a rectangular triangle, is equal to the amount of the squares constructed on its legs.

The simplest evidence of the theorem is obtained in case of an isosceles rectangular triangle. Possibly, the theorem also began with it.

Really, it is rather simple to look at a mosaic of isosceles rectangular triangles to be convinced of justice of the theorem. For example, for ΔABC: the square constructed on a hypotenuse the EXPERT, contains 4 initial triangles, and the squares constructed on legs, - on two. Thetheoremisproved.

ProofNo. 2Пусть Т - прямоугольный треугольник с катетами а , b и гипотенузой с (рис. а) . Докажем, что с² =а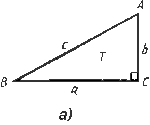² + Ь² .

We will construct Q square with the party а+Ь (fig.). On the parties of a square of Q we will take points And, In, With, D so that pieces of AVATARS, VS, CD, DA cut from a square Q rectangular triangles of T1, T2, T3, T4 with legs and and b. We will designate a quadrangle of ABCD a letter P. We will show that P - a square with side of the village.

All triangles of T1, T2, T3, T4 are equal to the T triangle (on two legs). Therefore their hypotenuses are equal to the T triangle hypotenuse, i.e. a page piece. We will prove that all corners of this quadrangle straight lines.

Let an and b - sizes of acute angles of a triangle T. Togda, as you know, a+b = 90 °. The corner in case of top And a quadrangle P together with the corners, equal an and b, constitutes the developed corner. Therefore a+b =180 °. And as a+b = 90 °, g=90 °. It is in the same way proved, as other corners of a quadrangle P straight lines. Therefore, a quadrangle P - a square with the page party.

Q square with the party а+Ь develops of a square P with the party with and four triangles equal to a triangle of T. Poetomu for their areas equality of S(Q)=S(P)+4S(T) is carried out.

As S(Q) = (a+b)2; To S (P) =c2 and S(T) = ½a*b, that, adding these expressions in S(Q)=S(P)+4S(T), we receive equality (a + b) 2 = c2 + 4*½a*b. As (a+b)2 =a2 +b2 +2*a*b, equality (a+b)2 =c 2+4*½a*b it is possible to write down so: a2 +b2 +2*a*b=c2 +2*a*b.

From equality of a2 +b2 +2*a*b=c2 +2*a*b follows that с2 =а2 + 2.

ч.т.д.

Proof No. 3

Let ΔАВС - this rectangular triangle with a right angle S. Provedem CD height from top of a right angle of Page.

By determination of a cosine of the angle (A cosine of an acute angle of a rectangular triangle the relation of an adjacent leg to a hypotenuse is called) sosa=ad/AC=AC/AB. From here AB*AD=AC2. Analogichnososv=bd/BC=BC/AB. From here AB*BD=BC2. Putting the received equalities term by term and noticing, чтоAD+DB=AB, we will receive: AC2 + BC2 =AB(AD + DB) = AB2. The theorem is proved.

Proof No. 4

The area rectangular треугольника:S =½*a*b or (p*r) S=½ (for any triangle);

p - полупериметр triangle; r - radius of the circle entered in it.

r = ½ * (a + b - c) - the radius of the circle entered in any triangle.

½*a*b = ½*p*r = ½ (a + b + c) *½ (a + b - c);

a*b = (a + b + c) *½ (a + b - c);

a + b=x;

a*b = ½ (x + c) * (x - c) *a*b = ½ (x2 - c2)

a*b = ½ (a2 + 2*a*b + b2 - c2)

a2 + b2 - c2 = 0, means

a2 + b2 = c2

Proof No. 5

ΔАВС - rectangular treugolnikaj - height lowered on gipotenuzubced - a square on gipotenuzeabfh and ACKJ - the squares constructed on legs.

To prove: The square of a hypotenuse is equal to the amount of squares of legs (Pythagorean theorem).

Proof: 1. We will prove that the rectangle of BJLD is equal to ABFH square, ΔABD =ΔBFS (on two parties and a corner of BF=AB between them; BC=BD; FBS=ABD corner). But! SΔABC = ½SBJLD, since at ΔABC and BJLD rectangle the general basis of BD and general height of LD. Similar to SΔFBS = ½SABFH (BF - the general basis, AB - general height). From here, considering that SΔABD = SΔFBS, we have: SBJLD = SABFH. Similarly, using equality of a triangle ΔBCK and ΔACE, it is proved that SJCEL = SACKG. So, SABFH + SACKJ = SBJLD + SBCED.

Now that the success of development of many areas of science and equipment depends on development of various directions of mathematics was generally recognized. An important condition of increase of production efficiency is widespread introduction of mathematical methods in equipment and a national economy that assumes creation of new, effective methods of high-quality and quantitative research which allow to solve the problems pushed by practice. We will review some elementary examples of such tasks in which in case of the decision Pythagorean theorem is applied.

Construction

Window

In buildings of Gothic and Romance style the upper parts of windows are dismembered by stone edges which not only play an ornament role, but also durabilities of windows promote. In drawing the simple example of such window in Gothic style is provided. The method of its creation is very simple: From drawing it is easy to find the centers of six arches of the circles which radiuses are equal to width of a window (b) for external arches and a half of width (b/2), for internal arches. There is still the complete circle concerning four arches. As it is concluded between two concentric circles, its diameter is equal to distance between these circles, i.e. b/2 and, therefore, radius is equal to b/4. And then becomes clear and a provision of its center. Radiuses were in the reviewed example without any difficulties. In other similar examples can потребоватися calculations; we will show how Pythagorean theorem is applied in such tasks.

In Romance architecture the motive provided in drawing often meets. If b still designates window width, radiuses of semi-circles will be equal to R = to b/2 and r = to b/4. Radius of p of an internal circle can be calculated from the rectangular triangle represented in fig. by a dotted line. The hypotenuse of this triangle passing through a point of a contact of circles, is equal to b/4+p, one leg is equal to b/4, and other b/2-p.

On Pythagorean theorem we have:

(b/4+p) = (b/4) + (b/4-p)

or

b/16 + b*p/2+p=b/16+b/4-b*p+p,

from where

b*p/2=b/4-b*p.

Having divided into b and bringing similar members, we will receive:

(3/2) *p=b/4, p=b/6.

Roof

In the house it is conceived to construct a dvuskatny roof (a form in section). What length there shall be rafters if beams of AC=8 m, and AB=BF are made.

Decision:

ADC triangle - isosceles AB=BC=4 m, BF=4 m If to assume that m FD=1,5, then:

A) From DBC triangle: DB=2,5м

B) From ABF triangle:

Lightning arrester

The lightning arrester protects all subjects the distance to which from its basis doesn't exceed its doubled height from a lightning. To determine an optimum provision of a lightning arrester on the dvuskatny roof, providing its the smallest available height.

Decision:

On h2 Pythagorean theorem ≥ a2 +b2, means h ≥ (a2 +b2) ½.

Answer: h ≥ (a2 +b2) ½

Astronomy

In this drawing points of A and B and a way of a light beam from A to B and back are shown. The way of a beam is shown by a curved arrow for descriptive reasons, actually, light beam - a straight line.

What way passes a beam? As light goes there and back identical way, we will ask directly: to that is a half of a way which passes a beam equal? If to designate AB piece a symbol l, time half as t, and also having designated the speed of movement of light a letter c, our equation will assume an air

with * t = l

Obviously? It after all work of spent time for speed!

Now we will try to look at the same phenomenon from other reference system, from other point of view, for example, from the spaceship which is flying by by a running beam with a speed of v. Earlier we understood that in case of such supervision of speed of all bodies will change, and motionless bodies will begin to move with v speed to the counter party. We will assume that the ship moves to the left. Then two points between which the hare runs, will begin to move to the right with the same speed. And, at that time, while the hare runs the way, the starting point of A is displaced and the beam returns already to a new point of C.

Question: on how many will be in time the point (to turn into a point of C) while the light beam travels will be displaced? More precisely, again we will ask about a half of this shift! If to designate a half of time of travel of a beam a letter t', and a half of distance of AC a letter d, we will receive our equation in a type:

v * t' = d

The letter v designated the speed of movement of the spaceship. Again obviously, isn't that so?

Other question: what way thus will pass a ray of light? (More precisely to that a half of this way is equal? To that the distance to unknown object is equal? )

If to designate a half of length of a way of light a letter s, we will receive the equation:

with * t' = s

Here with is a velocity of light, and t' is too it is a high time which we considered on formulas above.

Now we will consider ABC triangle. It is the isosceles triangle which height is equal to l. Yes, to that l which we entered by process consideration from the motionless point of view. As movement happens perpendicular to l, it couldn't affect not it.

The triangle of ABC is constituted from two halves - are identical the rectangular triangles which hypotenuses of AB and BC shall be connected with legs on Pythagorean theorem. One of legs is d which we calculated just, and the second leg is s which passes light and which we too calculated.

We receive the equation:

s2 = l2 + d2

It after all simply Pythagorean theorem, truly?

At the end of the nineteenth century various assumptions of existence of inhabitants of Mars similar to the person expressed, it was a consequence of opening of the Italian astronomer Skiaparelli (I opened channels which long time were considered artificial), etc. on Mars. It is natural that a question of, whether it is possible to speak by means of light signals with these hypothetical beings, I caused brisk discussion. The Parisian academy of Sciences even established an award in 100000 francs to the one who the first

Date: 2015-01-29; view: 902