
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Resistive circuits
Passive sign convention
In electronics, which deals with more passive than active devices, electric power consumed in a device is defined to have a positive sign, while power produced by a device is defined to have a negative sign. This is called the passive sign convention.
Resistive circuits
In the case of resistive (Ohmic, or linear) loads, Joule's law can be combined with Ohm's law (V = I·R) to produce alternative expressions for the dissipated power:
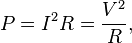
where R is the electrical resistance.
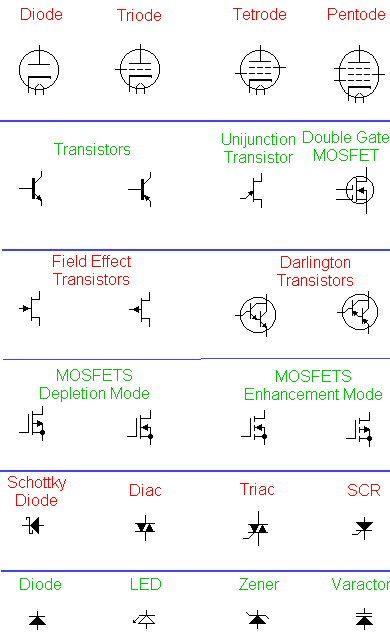
10. What is the difference between active and passive circuit elements? Give the examples of typical active and passive elements.
ACTIVE COMPONENTS
The components which produce the energy in the form of current or voltage are called as active components.
Example:transistors etc,.
PASSIVE COMPONENTS
The components which stores the energy in the form of current or voltage are called as passive components.
example:inductors,resistors,capacitors etc,.
The three linear passive elements are the Resistor, the Capacitor and the Inductor. Examples of non-linear passive devices would be diodes, switches and spark gaps. Examples of active devices are Transistors, Triacs, Varistors, Vacuum Tubes, relays, solenoids and piezo electric devices."
Active Circuit Elements:
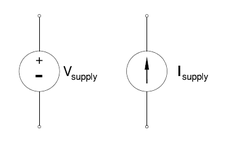
|
| Figure 1.1: Active circuit elements |
All circuit elements that are capable of supplying electric power to a circuit or to an aspect of the circuit for an indefinitely long time are called Active circuit elements. Batteries and generators are examples of active circuit elements. Figure 1.1 shows circuit symbols used to depict a Voltage Source (an ideal battery) and a Current Source. Notice that the circuit elements show a polarity—either a reference label for the voltage or an arrow giving a reference direction for the current or both. There is also a mathematical equation associated with each circuit element. For a voltage source, V = 5 volts (or any constant) is an example of such an equation. For a current source, I = 2 amperes (or any constant) is another example.
Transistors, vacuum tubes (valves), and many other circuit elements are also active elements even though they cannot supply electrical power to the entire circuit for an indefinitely long time. These components take electrical power from one part of the circuit (often called a power supply) and deliver the power to another part of the circuit (often by way of amplifying a signal) and can do this for an indefinitely long time.
Note that an element is active if it is capable of the above. Even if it is not delivering power to a particular circuit (or an aspect of a particular circuit) it might still be an active circuit element.
Passive Circuit Elements:
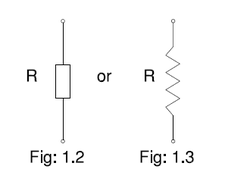
Philosophically speaking, any circuit element that is not active is passive. This means that passive circuit elements Absorb or Dissipate electric power in the long term. In the short term they may store some electric power and then return that power back to the circuit at a later time. Even if a circuit element is 100% efficient in this storage and return process, it is passive because it cannot deliver power over an indefinitely long time. (Of course nothing more than 100% efficient exists. Active circuit elements have a source of energy to draw on, such as the chemicals in a battery. Passive elements do not.) A resistor is a good example of a passive circuit element. The following picture shows circuit symbols used to depict a Resistor. The symbol shown in Figure 1.2 for a resistor is generally preferred in Europe and some other parts of the world and will be used throughout this course. The symbol shown in Figure 1.3 is generally (but not always) used in the Americas.
|
11. What is the difference between independent and dependent active elements? Draw the symbols for all active elements.
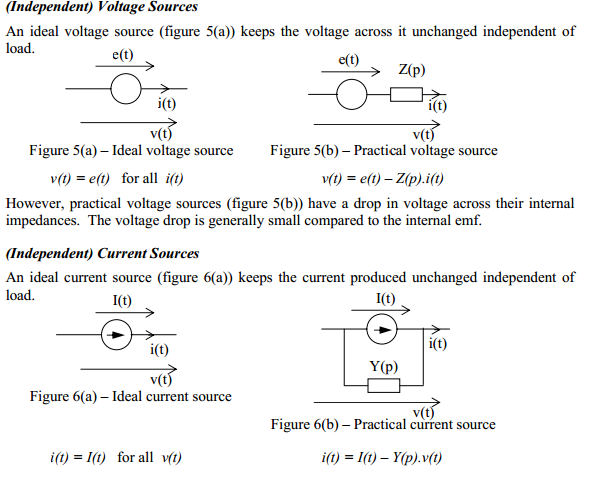
An independent voltage source is characterized by a terminal voltage which is
completely independent of the current through it
Another ideal source which we will need is the independent current
source. Here, the current through the element is completely independent of
the voltage across it
The two types of ideal sources that we have discussed up to now are called
independent sources because the value of the source quantity is not affected
in any way by activities in the remainder of the circuit. This is in contrast
with yet another kind of ideal source, the dependent, or controlled, source,
in which the source quantity is determined by a voltage or current existing
at some other location in the system being analyzed.
Passive Element: The element which receives energy (or absorbs energy) and then
either converts it into heat (R) or stored it in an electric (C) or magnetic (L ) field is
called passive element.
Active Element: The elements that supply energy to the circuit is called active element.
Examples of active elements include voltage and current sources, generators, and
electronic devices that require power supplies
12. Demonstrate the shortcomings of the mathematical model for the voltage source used to represent a real physical system. Why is it valid only under certain conditions?

consider the model for the voltage source in Fig. I. 14a. We assume that the voltage source delivers V volts regardless of what is connected to its terminals. Theoretically, we could adjust the external circuit so that an infinite amount of current would flow, and therefore the voltage source would deliver an infinite amount of power. This is, of course, physically impossible. A similar argument could be made for the independent current source. Keep in mind that models have limitations and thus are valid representations of physical systems only under certain conditions
13. Demonstrate the shortcomings of the mathematical model for the current source used to represent a real physical system. Why is it valid only under certain conditions?
14. Describe dependent sources.

15. Ohm’s law.

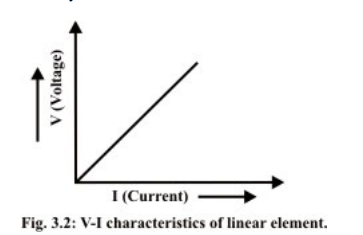
16. Graphical representation of the voltage-current relationships for a linear and a nonlinear resistor.
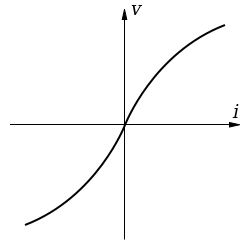 non-linear
non-linear 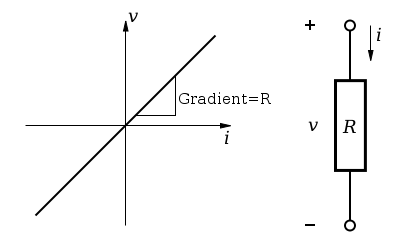
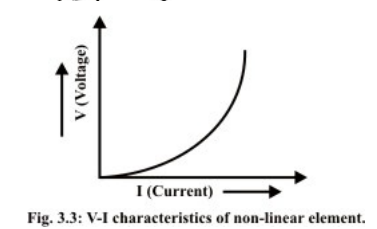
Non-Linear Circuit: Roughly speaking, a non-linear system is that whose parameters
change with voltage or current.
17. Mathematically prove that a resistor is a passive element.
Resistors are the most simple electronic devices. As we have already seen, each time a current flows in a material, there is a resistance, depending both on the intrinsic characteristics of the material as well as its geometry, that opposes the current flow. Resistors are components built to have a determined value of electrical resistance.
18. Short circuit and open circuit.
* An open circuit is where there is no current flow ans voltage tends to infinity.
* A short circuit is where the voltage tends to zero and current tends to infinity.
In an open circuit, no current flows and the voltage tends to the emf of whatever is generating the voltage. All sources of voltage have internal resistance and internal emf. When the circuit is open, there is no voltage drop across the internal resistance so the true internal emf is seen.
Open Circuit
An OPEN circuit is an incomplete electrical pathway. A cut in the wire, a blown fuse, anything that increases resistance to electricity somewhere in the path creates an open circuit. Note that cutting or disconnecting a portion of an electrical circuit creates an 'air gap' between the wiring or conductors. This air gap increases the electrical resistance of the circuit and breaks the electrical connection.
Closed Circuit
A closed circuit is a path which could allow electricity to flow across the circuit from an area of strong charge to an area of weak charge. It is important to remember that a closed circuit might not actually have an electrical current applied to it, but still be a closed circuit.
Short Circuit
A SHORT is when the electricity doesn't flow along the expected path. This could be because the connection is cross-connecting somewhere else, or grounding to another source of electricity. Simply put, the circuit is completing before it gets to where we actually want the electricity to flow to. This is why we talk about burnt wiring having shorted out.
19. Kirchhoff’s laws.

20. Node. Loop. Branch. Mesh.
Node
A circuit node is where two or more components are connected together with shorts. Figure below shows an example of a simple node. The lines are shorts that are connected to the other components in the circuit. A node acts like an intersection of flowing currents.
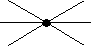
Similar to shorts, nodes have no electrical properties of their own and are only a mean to connect circuit parts together
Branch
A circuit branch is between any two nodes, consisting of one or more components connected in series. There would be no other branches connected in-between the two nodes of one branch. Figure below shows an example of a branches between nodes N1 and N2.

Mesh
A mesh in a circuit is any close loop starting and ending with the same node, not passing any node or branch twice. Figure below shows three different meshes for a circuit.
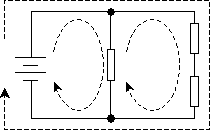
Loop=circuit
21. Voltage division and current division.

Applying Kirchhoff's voltage law to this circuit yields V(t) = v1, + v2, However, from Ohm's law we know that V1, = R1i(t) v2 = R2i(t) Therefore,V( t) = R1i(t ) + R2i(t) Solving the equation for i(t) yields 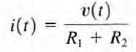 Knowing the current, we can now apply Ohm's law to determine the voltage across each resistor: V1, = R1i(t )
Knowing the current, we can now apply Ohm's law to determine the voltage across each resistor: V1, = R1i(t ) 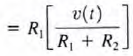
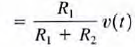
Equations are very important because they describe the operation of what is called a voltage divider. In other words, the source voltage v( t} is divided between the resistors R1 and R2 in direct proportion to their resistances.
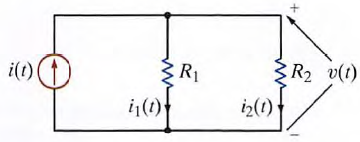
Applying Kirchhoff's current law to the upper node, we obtain i(t) = i1(t) + i2(t) and employing Ohm's law, we have 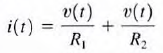
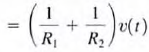
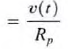
The manner in which the current i(r) from the source divides between the two branches is called current division and can be found from the preceding expressions
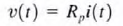
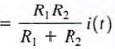 and
and 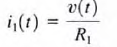 then
then 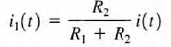
22. Series and parallel resistor combinations.
i. consider the circuit
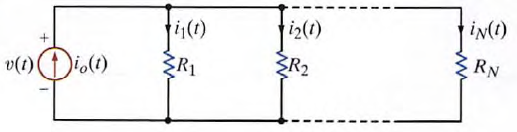 Now consider the circuit with N resistors in parallel. Applying Kirchhoff's current law to the upper node yields
Now consider the circuit with N resistors in parallel. Applying Kirchhoff's current law to the upper node yields 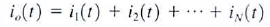
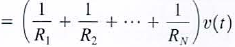 or
or 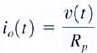 where
where 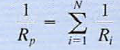
23. What are the node voltages in nodal analysis?
a. 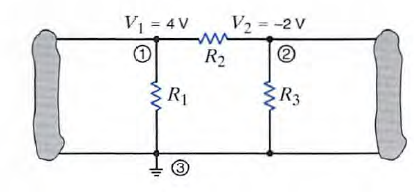
- The voltage VI = 4 V is the voltage at node 1 with respect to the reference node 3. Similarly. the voltage V2 = - 2 V is the voltage at node 2 with respect to node 3. In addition, however, the voltage at node 1 with respect to node 2 is +6 Y, and the voltage at node 2 with respect to node 1 is - 6 V. Furthermore, since the current will flow from the node of higher potential to the node of lower potential, the current in R1 is from top to bottom, the current in R2 is from left 10 right, and the current in R) is from bottom to top.
24. Reference and nonreference nodes in nodal analysis.
- In a nodal analysis, the variables in the circuit are selected to be the node voltages. The node voltages are defined With respect to a common point in the circuit. One node is selected as the reference node, and all other node voltages are defined with respect to that node. It is commonly called ground because it is said to be at ground-zero potential. We will select our variables as being positive with respect to the reference node. In a nodal analysis, we employ KCL equations. one of the nodes in an N-node circuit is selected as the reference node, and the voltages at all the remaining N - I nonreference nodes arc measured with respect to this reference node.
25. How to calculate the current through any resistive element knowing the node voltages at its terminals?
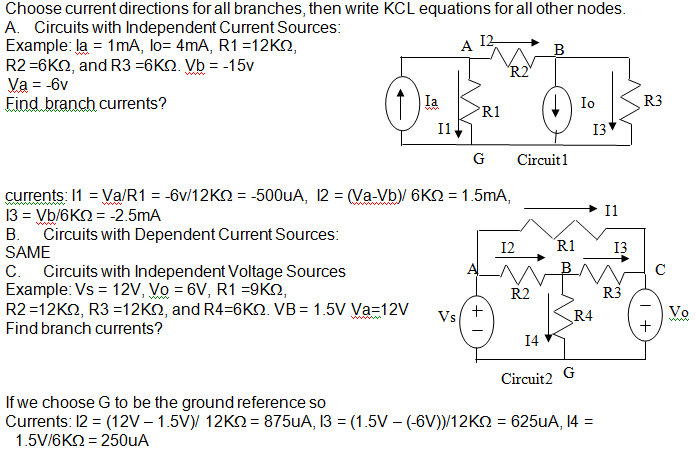
26. What is a loop current in loop analysis?
A mesh current is a current that loops around the essential mesh and the equations are set solved in terms of them. A mesh current may not correspond to any physically flowing current, but the physical currents are easily found from them.
27. Describe the algorithm of the nodal analysis for an N-node circuit.
a. Determine the number of nodes in the circuit. Select one node as the reference node. Assign a node voltage between each nonreference node and the reference node. All node Voltages are assumed positive with respect to the reference node. For an N-node circuit, there are N - J node voltages. As a result, N - I linearly independent equations must be written to solve for the node voltages.
b. Write a constraint equation for each voltage source independent or dependent- in the circuit in terms of the assigned node voltages using KVL. Each constraint equation represents one of the necessary linearly independent equations, and Nv voltage sources yield Nv linearly independent equations. For each dependent voltage source, express the controlling variable for that source in terms of the node voltages. A voltage source-independent or dependent-may be connected between a nonreference node and the reference node or between two nonreference nodes. A supernode is formed by a voltage source and its two connecting nonreference nodes.
c. Use KCL to formulate the remaining N - I - Nv linearly independent equations. First, apply KCL at each nonreference node not connected to a voltage source. Second, apply KCL at each supernode. Treat dependent current sources like independent current sources when formulating the KCL equations. For each dependent current source, express the controlling variable in tenns of the node voltages.
28. Describe the algorithm of the loop analysis for an N-loop circuit.
a. Determine the number of independent loops in the circuit. Assign a loop current to each independent loop. For an N-Ioop circuit, there are N-loop currents. As a result , N linearly independent equations must be written to solve for the loop current s.
b. If current sources are present in the circuit, either of two techniques can be employed. In the first case, one loop current is selected to pass through one of the current sources.The remaining loop currents are determined by open circuiting the current sources in the circuit and using this modified circuit to select them. In the second case, a current is assigned to each mesh in the circuit.
c. Write a constraint equation for each current source independent or dependent- in the circuit in terms of the assigned loop currents using KCL. Each constraint equation represents one of the necessary linearly independent equations, and Nt current sources yield Nt linearly independent equations. For each dependent current source, express the controlling variable for that source in terms of the loop currents.
d. Use KVL t0 formulate the remaining N - N/ linearly independent equations. Treat dependent voltage sources like independent voltage sources when formulating the KVL equations. For each dependent voltage source, express the controlling variable in terms of the loop currents.
29. Capacitor. Capacitance. Current and voltage relationship on capacitor.
A capacitor is a circuit element that consists of two conducting surfaces separated by a nonconducting, or dielectric, material. There are many different kinds of capacitors, and they are categorized by the type of dielectric material used between the conducting plates.
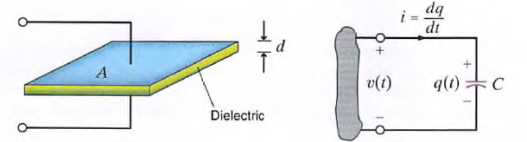
Capacitance is measured in coulombs per volt or farads. It is interesting to calculate the dimensions of a simple equivalent capacitor consisting of two
parallel plates each of area A, separated by a distance d 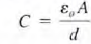 , where Eo' the permitivity of free space, is 8.85 X 10- " F / m.
, where Eo' the permitivity of free space, is 8.85 X 10- " F / m.
The charge on the capacitor is proportional to the voltage across it such that q = Cv
The charge differential between the plates creates an electric field that stores energy. Because of the presence of the dielectric, the conduction current that flows in the wires that connect the capacitor to the remainder of the circuit cannot flow internally between the plates. However. Via electromagnetic field theory it can be shown that this conduction current is equal to the displacement current that flows between the plates of the capacitor and is present any time that an electric field or voltage varies with time. (Since the current is 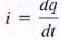 then for a capacitor
then for a capacitor 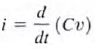 which for constant capacitance is
which for constant capacitance is 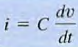 .eq can be rewritten as
.eq can be rewritten as 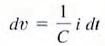 . Now integrating this expression from
. Now integrating this expression from  to some time t and assuming
to some time t and assuming  yields
yields 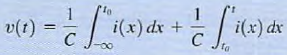
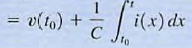 where V( to) is the voltage due to the charge that accumulates on the capacitor from time
where V( to) is the voltage due to the charge that accumulates on the capacitor from time 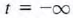 to time t= t0. The energy stored in the capacitor can be derived from the power that is delivered to the element. This power is given by the expression
to time t= t0. The energy stored in the capacitor can be derived from the power that is delivered to the element. This power is given by the expression 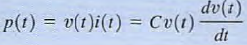 )
)
Derivating wrt time the last equation: 
This expression shows us that a constant voltage across a capacitor produces no current through the capacitor. Also we see that current and voltage are not in phase.
30. Describe the case of a dc voltage applied across a capacitor.
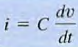 we see that the current flowing through the capacitor is direct ly proportional to the time rate of change of the voltage across the capacitor. A dc voltage does not vary with time, so the current flowing through the capacitor is zero. We can say that a capacitor is "an open circuit to de" or "blocks de." Capacitors are often utilized to remove or filter out an unwanted dc voltage. the power absorbed by a capacitor, is directly proportional to the time rate of change of the voltage across the capacitor. if we had an instantaneous change in the capacitor voltage This would correspond to dv/ dt =
we see that the current flowing through the capacitor is direct ly proportional to the time rate of change of the voltage across the capacitor. A dc voltage does not vary with time, so the current flowing through the capacitor is zero. We can say that a capacitor is "an open circuit to de" or "blocks de." Capacitors are often utilized to remove or filter out an unwanted dc voltage. the power absorbed by a capacitor, is directly proportional to the time rate of change of the voltage across the capacitor. if we had an instantaneous change in the capacitor voltage This would correspond to dv/ dt = 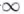 and infinite power. Since we only have finite power sources, the voltage across a capacitor cannot change instantaneously.
and infinite power. Since we only have finite power sources, the voltage across a capacitor cannot change instantaneously.
31. Mathematically prove that a capacitor is a passive element.
To determine whether component is passive , the total energy absorbed by it must be greater or equal zero 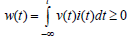 .the total capacitor energy is
.the total capacitor energy is 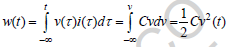 . It’s apparent that the total energy of the capacitor will be greater than zero if the capacitance greater than zero. Since the capacitance is dependent on capacitor construction, it cannot be negative. therefore, capacitor is passive element
. It’s apparent that the total energy of the capacitor will be greater than zero if the capacitance greater than zero. Since the capacitance is dependent on capacitor construction, it cannot be negative. therefore, capacitor is passive element
32. What is an idea of “continuity of voltage” for a capacitor?
the power absorbed by a capacitor, is directly proportional to the time rate of change of the voltage across the capacitor. if we had an instantaneous change in the capacitor voltage This would correspond to dv/ dt =  and infinite power. Since we only have finite power sources, the voltage across a capacitor cannot change instantaneously. This idea of "continuity of voltage for a capacitor tells us that the voltage across the capacitor just after a switch moves is the same as the voltage across the capacitor just before that switch moves.
and infinite power. Since we only have finite power sources, the voltage across a capacitor cannot change instantaneously. This idea of "continuity of voltage for a capacitor tells us that the voltage across the capacitor just after a switch moves is the same as the voltage across the capacitor just before that switch moves.
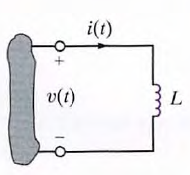
33. Inductor. Inductance. Current and voltage relationship on inductor.
a. An inductor is a circuit element that consists of a conducting wire usually in the form of a coil. An inductor is a device that stores energy in the magnetic field surrounding the inductor. Inductors are typically categorized by the type of core on which they are wound. Inductors made with air or nonmagnetic materials are widely used in radio, television
-
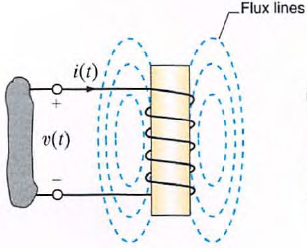
- (It was first shown that a current-carrying conductor would produce a magnetic field. it was later found that the magnetic field and the current that produced it were linearly related.. it was shown that a changing magnetic field produced a voltage that was proportional to the time rate of change of the current that produced the magnetic field
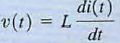 The constant of proportionality L is called the inductance and is measured in the unit henry, is dimensionally equal to 1 volt-second per ampere. we find that the expression for the current in an inductor is
The constant of proportionality L is called the inductance and is measured in the unit henry, is dimensionally equal to 1 volt-second per ampere. we find that the expression for the current in an inductor is 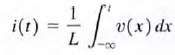 which can also be written as
which can also be written as 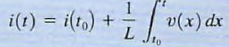
- The power delivered to the inductor can be used to derive the energy stored in the element. This power is equal to
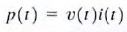
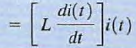 )
) - We have already seen that from Faraday’s law we obtain:
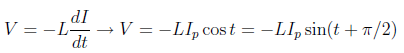 so again voltage and current are not in phase.
so again voltage and current are not in phase.
34. Describe the case of a dc current flowing through an inductor.
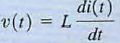 we see that the voltage across the inductor is direct ly proportional to the time rate of change of the current flowing through the inductor. A dc current does not vary with time,so the voltage across the inductor is zero. We can say that an inductor is "a short circuit to dc." we can replace any inductors with short circuits and calculate voltages and currents in the circuit
we see that the voltage across the inductor is direct ly proportional to the time rate of change of the current flowing through the inductor. A dc current does not vary with time,so the voltage across the inductor is zero. We can say that an inductor is "a short circuit to dc." we can replace any inductors with short circuits and calculate voltages and currents in the circuit
35. Mathematically prove that an inductor is a passive element.
The total inductor energy is 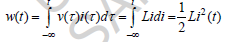 . Total energy of the inductor will be greater than zero if the inductance greater than zero. Since the inductance cannot be negative, inductor is passive element
. Total energy of the inductor will be greater than zero if the inductance greater than zero. Since the inductance cannot be negative, inductor is passive element
36. What is an idea of “continuity of current” for an inductor?
a. Note from 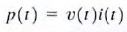
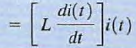 that an instantaneous change in inductor current would require in finite power. Since we don' t have any infinite power sources, the current flowing through an inductor cannot change instantaneously. This idea of "continuity of current" for an inductor tells us that the current flowing through an inductor just after a switch moves is the same as the current flowing through an inductor just before that switch moves.
that an instantaneous change in inductor current would require in finite power. Since we don' t have any infinite power sources, the current flowing through an inductor cannot change instantaneously. This idea of "continuity of current" for an inductor tells us that the current flowing through an inductor just after a switch moves is the same as the current flowing through an inductor just before that switch moves.
37. Prove that capacitors in series combine like resistors in parallel.
a. If a number of capacitors are connected in series, their equivalent capacitance can be calcu lated using KVL. For this circu it
b. 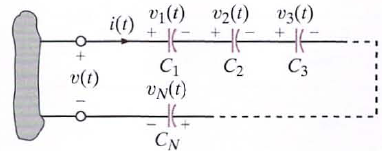
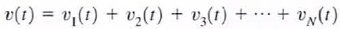 but
but 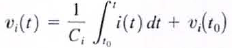 =>
=> 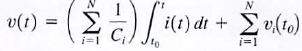
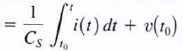 where
where 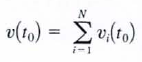 and
and 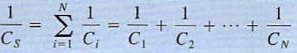
- since the same current flows in each of the series capacitors, each capacitor gains the same charge in the same time period. The voltage across each capacitor will depend on th is charge and the capacitance of the element
38. Prove that capacitors in parallel combine like resistors in series.
a. To determine the equivalent capacitance of N capacitors connected in parallel. we employ KCL.
b. 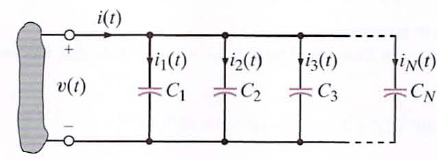
c. 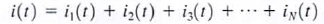
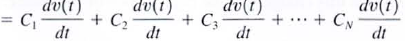
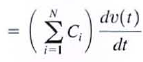
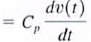
d. where 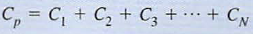
39. Prove that inductors in series combine like resistors in series.
a. If N inductors are connected in series. the equivalent inductance of the combination can be determined as follows. using KVL, we see that
b. 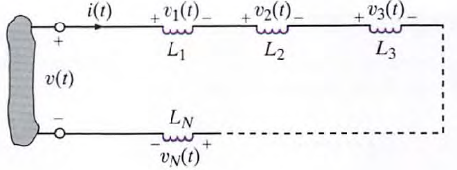
c. 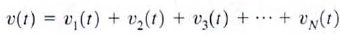 therefore
therefore 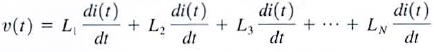
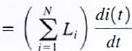
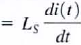 where
where 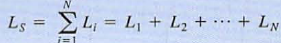
40. Prove that inductors in parallel combine like resistors in parallel.
a. 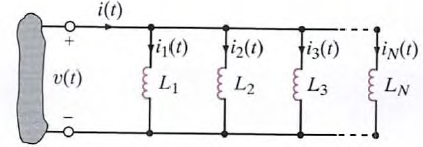
b. Consider the circuit which contains N parallel inductors. Using KCL, we can write 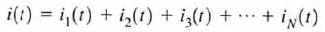 however
however
c. 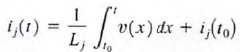 substituting to 1st eq
substituting to 1st eq 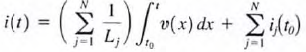
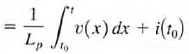 where
where 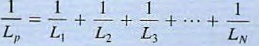
41. First-order circuits. Transition period. Steady-state value. Time constant.
An RC or RL transient circuit is said to be first order if it contains only a single capacitor or single inductor. The voltage or current anywhere in the network can be obtained by solving a first-order differential equation.
The function e - 1/1 decays to a value that is less than 1 % of its initial value after a period of ST. Therefore, the time constant, T, determines the time required for the circuit to reach steady state.
The time constant for an RC circuit is RTh C and for an RL circuit is L/RTh , where RTh is the Thevenin equivalent resistance looking into the circuit at the terminals of the storage element (i.e., capacitor or inductor).
42. Second-order circuits. Different techniques for performing a transient analysis.
For circuit1, the capacitor has no initial voltage, and 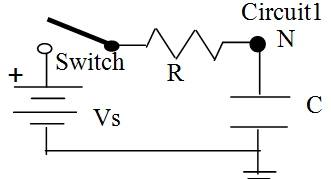
The switch closes at t=0s
For the RC capacitor circuit1 - write a KCL equation.
| L |
| Circuit2 |
| R |
| Switch |
| Vs |
| + |
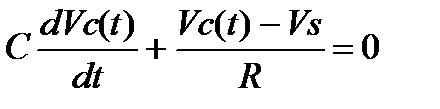
For circuit2, the inductor has no initial current, and
The switch closes at t=0s
For the RL inductor circuit2 – write a KVL equation.
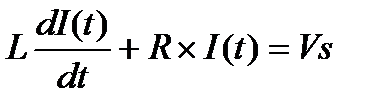
Use the general form solution for a first order differential equation 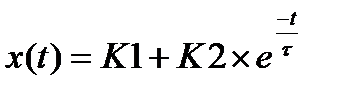
For this general form solution: K1 = steady state value (after a long time).
K2 = the initial condition. t = the time constant.
Using this general solution in the KCL equation: K1 = Vs, K2 = -Vs, and t = R x C
Using this general solution in the KVL equation: K1 = Vs / R, K2 = -Vs / R, and t = L / R
43. General form of the response equation for the first-order circuit.
For circuit1, the switch opens at t=to
For a parallel RLC circuit1 - write a KCL equation.
| L |
| Circuit2 |
| R |
| C |
| Vs |
| + |
| Sw |
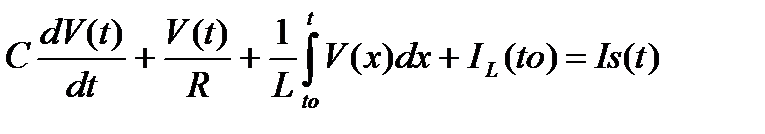
For circuit2, the switch closes at t=to
For series RLC circuit2 – write a KVL equation.
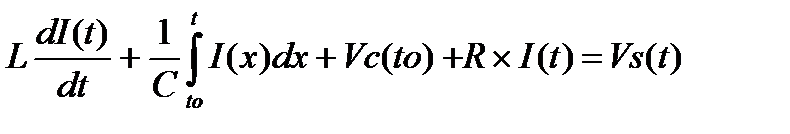
Since the initial conditions are constant, taking the derivative of these equations gives equations of the general form: 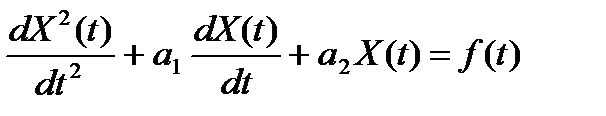
The homogeneous form: 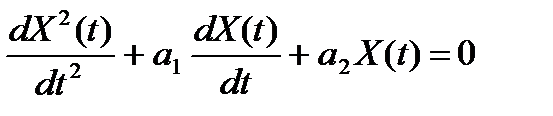
44. Describe the differential equation approach.
a. Equation 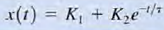 defines the general form of the solution of first-order transient circuits; that is, it represents the solution of åhe differential equation that describes an unknown current or voltage anywhere in the network
defines the general form of the solution of first-order transient circuits; that is, it represents the solution of åhe differential equation that describes an unknown current or voltage anywhere in the network
Consider the circuit 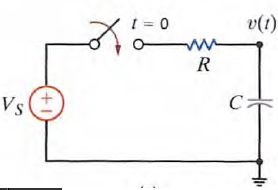 At time t = 0, the switch closes. The KCL equation that describes the capacitor voltage for time t > 0 is
At time t = 0, the switch closes. The KCL equation that describes the capacitor voltage for time t > 0 is 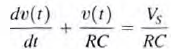 we assume that the solution of this first-order differential equation is of the form V(t)=K1+K2 e-t/τ Substituting this solution into the differential equation yields
we assume that the solution of this first-order differential equation is of the form V(t)=K1+K2 e-t/τ Substituting this solution into the differential equation yields 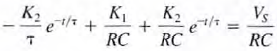 Equaling the constant and exponential terms, we obtain K1= Vs τ= RC Therefore,
Equaling the constant and exponential terms, we obtain K1= Vs τ= RC Therefore, 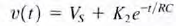 K2 is determined by the initial condition of the capacitor
K2 is determined by the initial condition of the capacitor
45. Describe the step-by-step approach.
a. Step 1. We assume a solution for the variable X(t) of the form X(t) = K, + K, e-t/τ
b. Step 2. Assuming that the original circuit has reached steady state before a switch was thrown, draw this previous circuit with the capacitor replaced by an open circuit or the inductor replaced by a short circuit. Solve for the voltage across the capacitor, vc(o-), or the current through the inductor, iL(o- ), prior to switch action.
c. Step 3. Draw the circuit valid for t = 0+ with the switches in their new positions. Replace a capacitor with a voltage source vc(O+) = vc(o-) or an inductor with a current source of value iL(O+) = iL(o-). Solve for the initial value of the variable x(o+ ).
d. Step 4. Assuming that steady state has been reached after the switches are thrown, draw the equivalent circuit, valid for t > 5τ, by replacing the capacitor by an open circuit or the inductor by a short circuit. Solve for the steady-state value of the variable 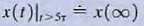
e. Step 5. Since the time constant for all voltages and currents in the circuit will be the same, it can be obtained by reducing the entire circuit to a simple series circuit containing a voltage source, resistor, and a storage element (i.e., capacitor or inductor) by forming a simple Thevenin equivalent circuit at the terminals of the storage element. This Thevenin equivalent circuit is obtained by looking into the circuit from the terminals of the storage element. The time constant for a circuit containing a capacitor is T = RTh C, and for a circuit containing an inductor it is t = L/ RTh –
f. Step 6. we can evaluate the constants in step 1 as x(O+) = K, + K, 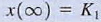 Therefore,
Therefore,  , and hence the solution is
, and hence the solution is 
46. Unit step function. Application of unit step function to circuit analysis.
The unit step function u(t) was defined as 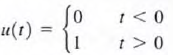
 corresponds to closing
corresponds to closing
a switch at t = 0 and connecting a voltage source of I V or a current source of 1 A to a given circuit.
47. Unit impulse function. Application of unit impulse function to circuit analysis.
The unit impulse function can be represented in the limit by the rectangular pulse 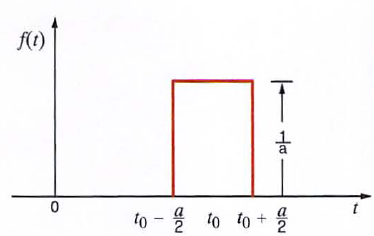 as a -> 0. The function is defined by the following
as a -> 0. The function is defined by the following 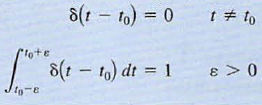 The unit impulse is zero except at t = t0, where it is undefined, but it has unit area. An important propert y of the unit impulse function is what is often called the sampling
The unit impulse is zero except at t = t0, where it is undefined, but it has unit area. An important propert y of the unit impulse function is what is often called the sampling 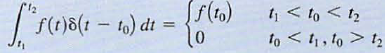
property, which is exhibited by the following integral for a finite to and any f(t) continuous at t0, Note that the unit impulse function simply samples the value of f(t) at t = t0
48. General form of the response equation for the second-order circuit.
- a general rule, for this case we are confronted with an equation of the form
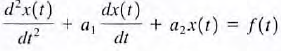 for homogeneous system
for homogeneous system 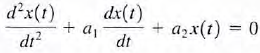 where a1 and a2 are constants. For simplicity we will rewrite the equation in the form
where a1 and a2 are constants. For simplicity we will rewrite the equation in the form 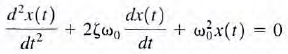 the solution must be a function whose first- and second-order derivatives have the same form , so that the left-hand side of equation will become identically zero for all t. Again we assume that
the solution must be a function whose first- and second-order derivatives have the same form , so that the left-hand side of equation will become identically zero for all t. Again we assume that 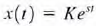 substituting yields
substituting yields 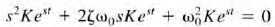 Dividing both sides of the equation by Kest yields
Dividing both sides of the equation by Kest yields 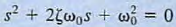 This equation is commonly called the characteristic equation ζ is called the exponential damping ratio, and w0 is referred to as the undamped natural frequency.
This equation is commonly called the characteristic equation ζ is called the exponential damping ratio, and w0 is referred to as the undamped natural frequency.
49. Overdamped form of the unforced response.
ζ> 1 The natural frequencies s1 and s2 are real and unequal; therefore, the natural response of the network described by the second-order differential equation is of the form 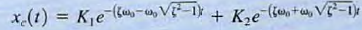 where K1 and K2 are found from the initial conditions. This indicates that the natural response is the sum of two decaying exponentials.
where K1 and K2 are found from the initial conditions. This indicates that the natural response is the sum of two decaying exponentials.
Underdamped form of the unforced response.
a. ζ<1 the natural frequencies are complex numbers. The natural response is then of the form 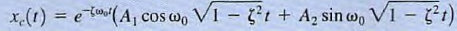 where A1 and A2, like K1 and K2 are constants. which are evaluated using the initial conditions x(O) and dx(O) / dt. This illustrates that the natural response is an exponentially dampedoscillatory response.
where A1 and A2, like K1 and K2 are constants. which are evaluated using the initial conditions x(O) and dx(O) / dt. This illustrates that the natural response is an exponentially dampedoscillatory response.
Critically damped form of the unforced response.
ζ=1 results in 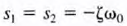 In the case where the characteristic equation has repeated roots, the general solution is of the form
In the case where the characteristic equation has repeated roots, the general solution is of the form  where BI and B2 are constants derived from the initial conditions.
where BI and B2 are constants derived from the initial conditions.
50. Underdamped form of the unforced response.
a. ζ<1 the natural frequencies are complex numbers. The natural response is then of the form 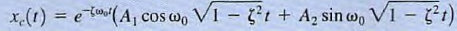 where A1 and A2, like K1 and K2 are constants. which are evaluated using the initial conditions x(O) and dx(O) / dt. This illustrates that the natural response is an exponentially dampedoscillatory response.
where A1 and A2, like K1 and K2 are constants. which are evaluated using the initial conditions x(O) and dx(O) / dt. This illustrates that the natural response is an exponentially dampedoscillatory response.
51. Critically damped form of the unforced response
ζ=1 results in 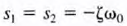 In the case where the characteristic equation has repeated roots, the general solution is of the form
In the case where the characteristic equation has repeated roots, the general solution is of the form  where BI and B2 are constants derived from the initial conditions.
where BI and B2 are constants derived from the initial conditions.
52. General expression for a sinusoidal function. Amplitude. Angular frequency. Period. Phase.
a. X(t ) = Xm sin wt where X(t) could represent either v{t) or i(t). Xm is the amplitude, maximum value or peak value, w is the angular frequency, and wt is the argument of the sine function
- X[w(t + T)] = X(wt)
-
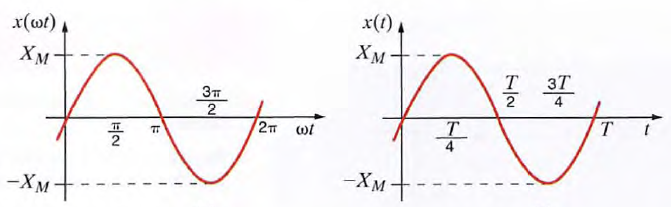
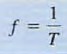
let us consider the following general expression for a sinusoidal function: X(t) = Xm sin (wt+ϴ) In this case (WI + 8) is the argument of the sine function, and ϴ is called the phase angle. 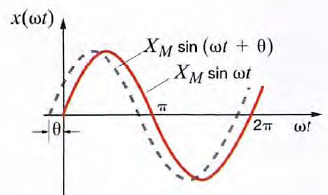 Because of the presence of the phase angle, any point on the waveform
Because of the presence of the phase angle, any point on the waveform
Xmsin(wt + ϴ) occurs ϴ radians earlier in time than the corresponding point on the waveform Xmsinwt . Therefore, we say that Xmsinwt lags Xmsin (Wt + ϴ) by ϴ radians.
53. Three conditions that must be satisfied before determining the phase difference.

54. How to establish a relationship between time-varying sinusoidal functions and complex numbers.


55. Phasors. Phasor analysis. Time domain. Frequency domain.
A phasor is a tool to relate the amplitude of a wave to the phase of a wave. For example, if you remove the time dependence from a sin wave and just look at the spatial dependence, and you write it in phasor form, you can say I(r) = A*exp{-jkr} where A is the wave's amplitude, r, the direction of propagation, k the propagation constant. Now, if you map this in polar form (the phase, phi, is simply k*r), you'll get a circle, where you can say the y-axis represent imaginary space, and the x-axis real space. You can then see as you trace around the circle, and look at the projection onto the real axis (x-axis), the amplitude grows and shrinks as you go around the circle. In fact, if you were to plot this changing in amplitude vs. space, you'd just get a sin wave.


A phasor is a polar representation of a complex number. Instead of real and imaginary components, you have a magnitude and a phase angle.
If the phase angle varies linearly with time, that is precisely the mapping into the frequency domain.
(a 4 Hz phasor will have its phase rotate by 360 degrees every quarter of a second)
Also, (in communication theory) instantaneous frequency is just the time derivative of the phase.
56. Phasor relationship for a resistor.
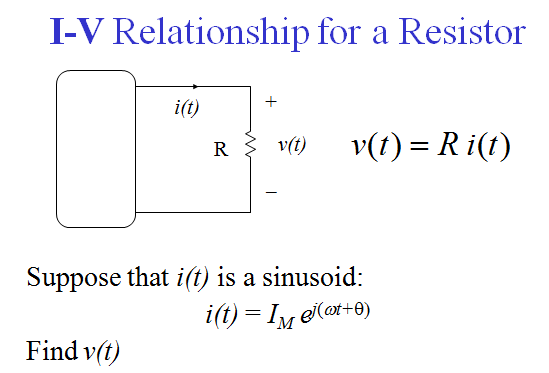
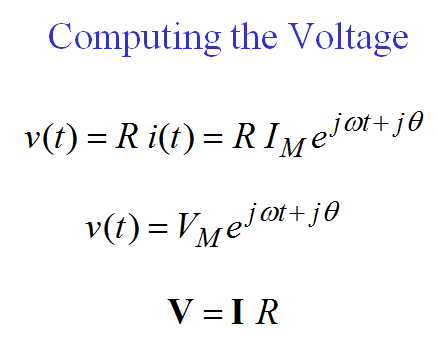
57. Phasor relationship for an inductor.
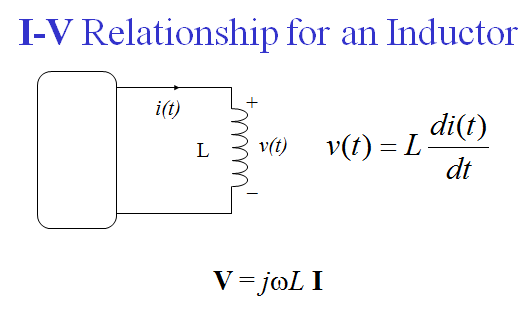
58. Phasor relationship for a capacitor.



59. Impedance and admittance.
Impedance (Z) is the over-all measure of the ability of a circuit to resist the flow of alternating current under a given a.c. voltage excitation. It may be expressed as Z = V / I where V and I are the a.c. voltage applied to and current flowing through the circuit. Its unit of measurement is the ohm (volt/ampere).
Admittance (Y) is the reciprocal of reactance, i.e., Y = 1 / Z. The unit of measurement for admittance is the siemens (S).
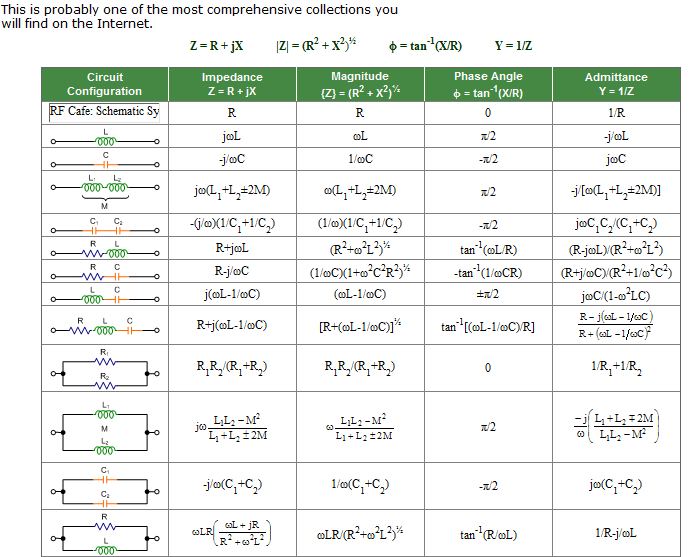
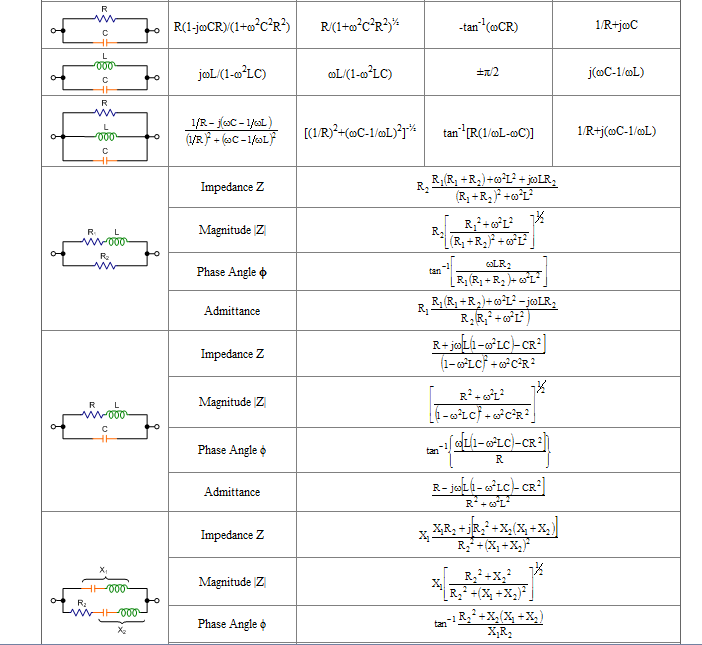

60. Impedances for different passive elements.
a. 
61. Resistance. Reactance. Conductance. Susceptance.
If you studied Resistance, Reactance, and Impedance, then you have a pretty good start in the basics of opposition to electric current. However, these three forces each have a twin, which is essentially their opposite. While resistance, reactance, and impedance all tend to restrict how much electricity can flow through a certain path, conductance, susceptance, and admittance are all forces that tend to allow electricity to flow. And there's good news: All of these forces are quite easy to understand and mathematically calculate.
Conductance is the opposite of resistance. While resistance is the restriction of current because of the chemical composition of a substance, conductance is the ability to conduct electricity of a certain material. Conductance is measured in siemens (S). Conductance is the reciprocal of resistance; That is to say, conductance is 1 divided by resistance. For example, if you have a 1,000 ohm resistor, its conductance is 1 divided by 1000, or 0.001 siemens. (This would probably be expressed by an engineer as 1 mS, one millisiemen.) The conductance of a 470 ohm resistor is about 2.13 mS. Notice that as resistance goes down, conductance goes up. Conductance's electrical symbol is G.
62. Instantaneous power.
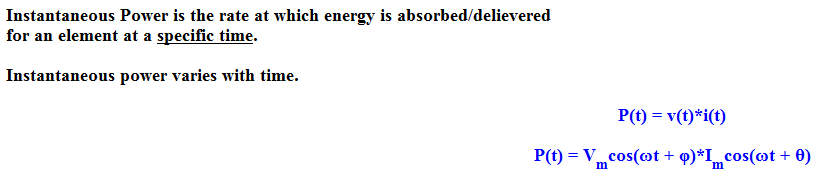
63. Average power.
The average over time of a modulated signal. The average power (often simply called "power" when the context makes it clear) is the average amount of work done or Energy transferred per unit time. Fiber optic power meters are instruments that measure the average power of a continuous Light beam. They are used to test signal power in fiber optic networks. 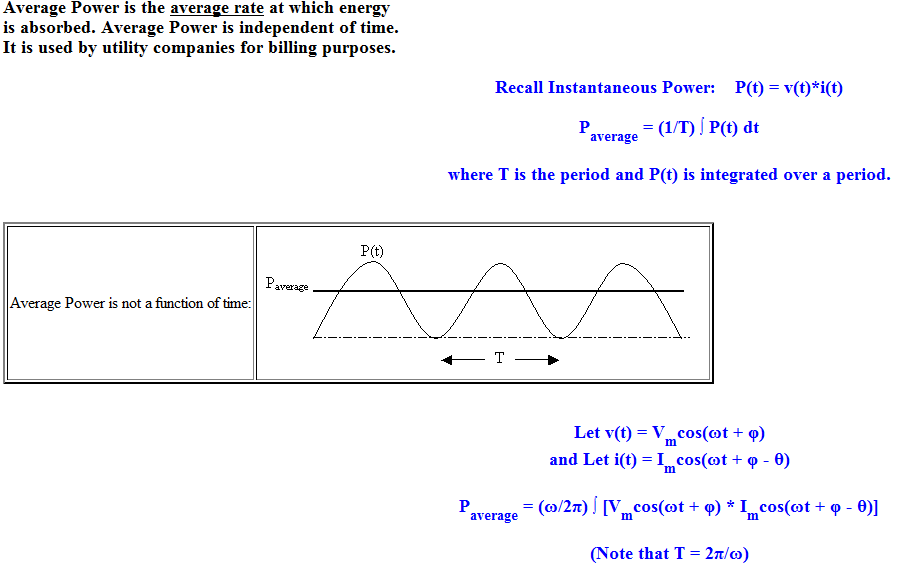
64. Superposition is not applicable to power. Why?
The superposition theorem states that in a linear circuit with several sources, the current and voltage for any element in the circuit is the sum of the currents and voltages produced by each source acting independently.
To calculate the contribution of each source independently, all the other sources must be removed and replaced without affecting the final result. When removing a voltage source, its voltage must be set to zero, which is equivalent to replacing the voltage source with a short circuit. When removing a current source, its current must be set to zero, which is equivalent to replacing the current source with an open circuit.
When you sum the contributions from the sources, you should be careful to take their signs into account. It is best to assign a reference direction to each unknown quantity, if it is not already given. The total voltage or current is calculated as the algebraic sum of the contributions from the sources. If a contribution from a source has the same direction as the reference direction, it has a positive sign in the sum; if it has the opposite direction, then a negative sign.
Note that If the voltage or current sources have internal resistance, it must remain in the circuit and still be considered. In TINA, you can assign an internal resistance to the DC voltage and current sources, while using the same schematic symbol. Therefore, if you want to illustrate the superposition theorem and at the same time use sources with internal resistance, you should only set the source voltage (or current) to zero, which leaves the source internal resistance intact. Alternatively, you could replace the source with a resistor equal to its internal resistance.
In order to use the superposition theorem with circuit currents and voltages, all of the components must be linear; that is, for all resistive components, the current must be proportional to the applied voltage (satisfying Ohm’s law).
Note that the superposition theorem is not applicable to power, since power is not a linear quantity. The total power delivered to a resistive component must be determined using the total current through or the total voltage across the component and cannot be determined by a simple sum of the powers produced by the sources independently.
65. Maximum average power transfer.
Sometimes in engineering we are asked to design a circuit that will transfer the maximum power to a load from a given source. According to the maximum power transfer theorem, a load will receive maximum power from a source when its resistance (RL) is equal to the internal resistance (RI) of the source. If the source circuit is already in the form of a Thevenin or Norton equivalent circuit (a voltage or current source with an internal resistance), then the solution is simple. If the circuit is not in the form of a Thevenin or Norton equivalent circuit, we must first use Thevenin’s or Norton’s theorem to obtain the equivalent circuit.
66. Effective or rms values.
The root-mean-square (rms) value or effective value of an ac waveform is a measure of how effective the waveform is in producing heat in a resistance.
Example: If you connect a 5 Vrms source across a resistor, it will produce the same amount of heat as you would get if you connected a 5 V dc source across that same resistor. On the other hand, if you connect a 5 V peak source or a 5 V peak-to-peak source across that resistor, it will not produce the same amount of heat as a 5 V dc source.
That's why rms (or effective) values are useful: they give us a way to compare ac voltages to dc voltages.
To show that a voltage or current is an rms value, we write rms after the unit: for example, Vrms = 25 V rms.
67. Apparent power. Power factor.
The power factor of an AC electrical power system is defined as the ratio of the real power flowing to the load to the apparent power in the circuit,[1][2] and is a dimensionless number between 0 and 1. Real power is the capacity of the circuit for performing work in a particular time. Apparent power is the product of the current and voltage of the circuit. Due to energy stored in the load and returned to the source, or due to a non-linear load that distorts the wave shape of the current drawn from the source, the apparent power will be greater than the real power.
In an electric power system, a load with a low power factor draws more current than a load with a high power factor for the same amount of useful power transferred. The higher currents increase the energy lost in the distribution system, and require larger wires and other equipment. Because of the costs of larger equipment and wasted energy, electrical utilities will usually charge a higher cost to industrial or commercial customers where there is a low power factor.
68. Complex power.


69. The Laplace transform. The inverse Laplace transform. Give an example of transform pair.
The Laplace transform is a widely used integral transform with many applications in physics and engineering. Denoted 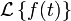 , it is a linear operator of a function f(t) with a real argument t (t ≥ 0) that transforms it to a function F(s) with a complex argument s. This transformation is essentially bijective for the majority of practical uses; the respective pairs of f(t) and F(s) are matched in tables. The Laplace transform has the useful property that many relationships and operations over the originals f(t) correspond to simpler relationships and operations over the images F(s).
, it is a linear operator of a function f(t) with a real argument t (t ≥ 0) that transforms it to a function F(s) with a complex argument s. This transformation is essentially bijective for the majority of practical uses; the respective pairs of f(t) and F(s) are matched in tables. The Laplace transform has the useful property that many relationships and operations over the originals f(t) correspond to simpler relationships and operations over the images F(s). 
70. The initial-value theorem. The final-value theorem.
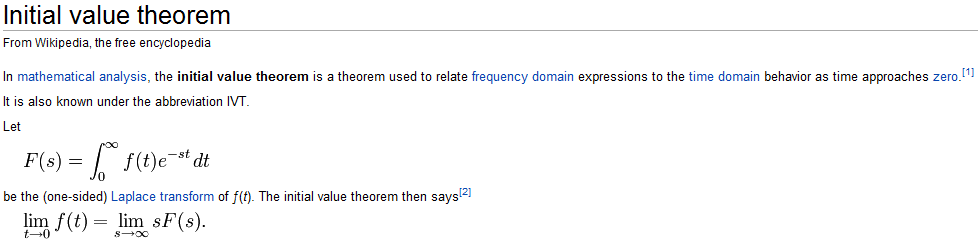

71. The s-domain equations for the capacitor. 
72. The s-domain equations for the inductor. 
73. Transfer (network) function. Importance of transfer function. Relationship between the roots of characteristic equation for the natural response of a second-order network and transfer function.
a. It is essentially nothing more than the ratio of some output variable to some input variable. if both variables are voltages, the transfer function is a voltage gain. If both variables are currents, the transfer function is a current gain. If one variable is a voltage and the other is a current, the transfer function becomes a transfer admittance or impedance. if only a single storage element is present, the natural response of a network to an initial condition is always of the form x( t ) = X0e-t/τ where x(t) can be either v(t) or i(t), X0 is the initial value of X(t). and T is the time constant of the network. We also found that the natural response of n second-order network is controlled by the roots of the characteristic equation, which is of the form  where ζ is the damping ratio and w0 is the undamped natural frequency
where ζ is the damping ratio and w0 is the undamped natural frequency
b. Case 1, ζ >1: Overdamped Network The roots of the characteristic equation are 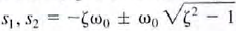 and, therefore, the network response is of the form
and, therefore, the network response is of the form 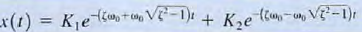
c. Case 2, ζ < 1: Underdamped Network The roots of the characteristic equation are 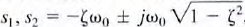 and, therefore . the network response is of the form
and, therefore . the network response is of the form 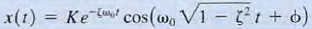
- Case 3, ζ=1: Critically Damped Network The roots of the characteristic equation are
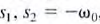 and, hence, the response is of the form
and, hence, the response is of the form 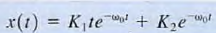
74. How to express any periodic function as a sum of sinusoidal functions? Fourier series.


75. Exponential Fourier series.


76. Trigonometric Fourier series.





77. Symmetry and the trigonometric Fourier series.


78. Examine the effect of time-shifting a periodic waveform defined by the exponential Fourier series.
i. the effect of time-shifting a periodic waveform f(t ) defined by the equation 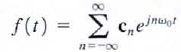 Note that
Note that  Since e -jnw0t0 corresponds to a phase shift, the Fourier coefficients of the time-shifted function are the Fourier coefficients of the original function, with the angle shifted by an amount directly proportional to frequency. Therefore, time shift in the time domain corresponds to phase shift in the frequency domain. we can compute the phase shift in degrees using the expression
Since e -jnw0t0 corresponds to a phase shift, the Fourier coefficients of the time-shifted function are the Fourier coefficients of the original function, with the angle shifted by an amount directly proportional to frequency. Therefore, time shift in the time domain corresponds to phase shift in the frequency domain. we can compute the phase shift in degrees using the expression 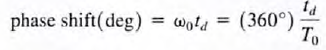
79. Frequency spectrum.
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.
Any signal that can be represented as an amplitude that varies with time has a corresponding frequency spectrum. This includes familiar concepts such as visible light (color), musical notes, radio/TV channels, and even the regular rotation of the earth. When these physical phenomena are represented in the form of a frequency spectrum, certain physical descriptions of their internal processes become much simpler. Often, the frequency spectrum clearly shows harmonics, visible as distinct spikes or lines, that provide insight into the mechanisms that generate the entire signal.
80. The Fourier transform. The inverse Fourier transform. Give an example of transform pair.


81. The principle of superposition.
The Superposition Principle states that in any linear network composed of resistors and voltage sources, the voltage across a resistor is simply the sum of all the voltages individually applied to it by each voltage source in the circuit. The superposition principle is a useful method for finding the voltage across any resistor in a network where more than one voltage source is present. A voltage source in this context may refer to any source of voltage or voltage signal, e.g., power supplies, batteries, oscillators, signal generato
Date: 2015-01-29; view: 7098
| <== previous page | | | next page ==> |
| Income elasticity of demand. Cross elasticity of demand. Characteristics of goods. | | | Shopaholic Abroad (by Sophie Kinsella) |