
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
The Linear Momentum of a System of Particles
Now consider a system of 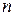 particles, each with its own mass, velocity, and linear momentum. The particles may interact with each other, and external forces may act on them as well. The system as a whole has a total linear momentum
particles, each with its own mass, velocity, and linear momentum. The particles may interact with each other, and external forces may act on them as well. The system as a whole has a total linear momentum  , which is defined to be the vector sum of the individual particles' linear momenta. Thus,
, which is defined to be the vector sum of the individual particles' linear momenta. Thus,
 (9-24)
(9-24)
If we compare this equation with Eq. 9-17, we see that
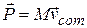 (linear momentum, system of particles), (9-25)
(linear momentum, system of particles), (9-25)
which gives us another way to define the linear momentum of a system of particles:
The linear momentum of a system of particles is equal to the product of the total mass  of the system and the velocity of the center of mass.
of the system and the velocity of the center of mass.
If we take the time derivative of Eq. 9-25, we find
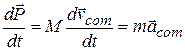 (9-26)
(9-26)
Comparing Eqs. 9-14 and 9-26 allows us to write Newton's second law for a system of particles in the equivalent form
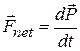 (9-27)
(9-27)
where 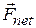 is the net external force acting on the system. This equation is the genşeralization of the single-particle equation
is the net external force acting on the system. This equation is the genşeralization of the single-particle equation  to a system of many particles.
to a system of many particles.
 9-6 Conservation of Linear Momentum
9-6 Conservation of Linear Momentum
Suppose that the net external force acting on a system of particles is zero (the system is isolated) and that no particles leave or enter the system (the system is closed). Putting  in Eq. 9-27 then yields
in Eq. 9-27 then yields 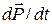 , or
, or
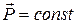 (closed, isolated system). (9-29)
(closed, isolated system). (9-29)
In words,
If no net external force act on a system of particles, the total linear momentum  of the system cannot change.
of the system cannot change.
This result is called the law of conservation of linear momentum. It can also be written as
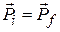 (closed, isolated system). (9-30)
(closed, isolated system). (9-30)
In words, this equation says that, for a closed, isolated system,
(total linear momentum at some initial time 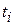 ) = (total linear momentum\ at some later time
) = (total linear momentum\ at some later time 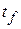 )
)
Equations 9-29 and 9-30 are vector equations and, as such, each is equivalent to three equations corresponding to the conservation of linear momentum in three mutually perpendicular directions as in, say, the xyz coordinate system. Depending on the forces acting on a system, linear momentum might be conserved in one or two directions but not in all directions. However,
It the component of the net external force on a closed system is zero along an axis, then the component of the linear momentum of the system along that axis cannot change.
As an example, suppose that you toss a grapefruit across a room. During its flight, the only external force acting on the grapefruit (which we take as the system) is the gravitational force  , which is directed vertically downward. Thus, the vertical component of the linear momentum of the grapefruit changes, but since no horizontal external force acts on the grapefruit, the horizontal component of the linear momentum cannot change.
, which is directed vertically downward. Thus, the vertical component of the linear momentum of the grapefruit changes, but since no horizontal external force acts on the grapefruit, the horizontal component of the linear momentum cannot change.
Note that we focus on the external forces acting on a closed system. Although internal forces can change the linear momentum of portions of the system, they cannot change the total linear momentum of the entire system.
ĽCHECKPOINT 4: An initially stationary device lying on a frictionless floor explodes into two pieces, which then slide across the floor. One piece slides in the positive direction of an x axis, (a) What is the sum of the momenta of the two pieces after the explosion? (b) Can the second piece move at an angle to the x axis? (c) What is the direction of the momentum of the second piece?


 Sample Problem 9-5
Sample Problem 9-5
A ballot box with mass 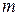 = 6.0 kg slides with speed
= 6.0 kg slides with speed  = 4.0 m/s across a frictionless floor in the positive direction of an x axis. It suddenly explodes into two pieces. One piece, with mass
= 4.0 m/s across a frictionless floor in the positive direction of an x axis. It suddenly explodes into two pieces. One piece, with mass 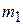 = 2.0 kg, moves in the positive direction of the x axis with speed
= 2.0 kg, moves in the positive direction of the x axis with speed 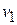 = 8.0 m/s. What is the velocity of the second piece, with mass
= 8.0 m/s. What is the velocity of the second piece, with mass 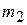 ?
?
SOLUTION: There are two Key Ideas here. First, we could get the velocity of the second piece if we knew its momentum, because we already know its mass is  kg. Second, we can relate the momenta of the two pieces to the original momentum of the box if momentum is conserved. Let's check.
kg. Second, we can relate the momenta of the two pieces to the original momentum of the box if momentum is conserved. Let's check.
Our reference frame will be that of the floor. Our system, which consists initially of the box and then of the two pieces, is closed but is not isolated, because the box and pieces each expellee a normal force from the floor and a gravitational force. However, those forces are both vertical and thus cannot change the horizontal component of the momentum of the system. Neither can the forces produced by the explosion, because those forces are internal to the system. Thus, the horizontal component of the momentum of the system is conserved, and we can apply Eq. 9-30 along the x axis.
The initial momentum of the system is that of the box:
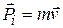 .
.
Similarly, we can write the final momenta of the two pieces as
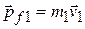 and
and 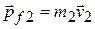 .
.
The final total momentum 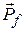 of the system is the vector sum of the momenta of the two pieces:
of the system is the vector sum of the momenta of the two pieces:
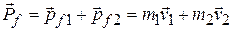 .
.
Since all the velocities and momenta in this problem are vectors along the x axis, we can write them in terms of their x components. Doing so while applying Eq. 9-30, we now obtain
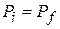
Or 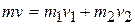 .
.
Inserting known data, we find
(6.0 kg)(4.0 m/s) = (2.0 kg)(8.0 m/s) + (4.0 kg)v2
and thus v2 = 2.0 m/s. (Answer)
Since the result is positive, the second piece moves in the positive direction of the x axis.
Sample Problem 9-6
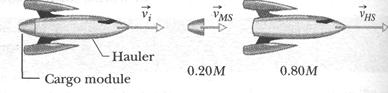
Figure 9-9a shows a space hauler and cargo module, of total mass  traveling along an
traveling along an  axis in deep space. They have an initial velocity
axis in deep space. They have an initial velocity  of magnitude 2100 km/h relative to the Sun. With a small explosion, the hauler ejects the cargo module, of mass 0.20M (Fig. 9-9b). The hauler then travels 500 km/h faster than the module along the x axis; that is, the relative speed
of magnitude 2100 km/h relative to the Sun. With a small explosion, the hauler ejects the cargo module, of mass 0.20M (Fig. 9-9b). The hauler then travels 500 km/h faster than the module along the x axis; that is, the relative speed 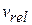 between the hauler and the module is 500 km/h. What then is the velocity
between the hauler and the module is 500 km/h. What then is the velocity  of the hauler relative to the Sun?
of the hauler relative to the Sun?
|
SOLUTION: The Key Idea here is that, because the hauler-module system is closed and isolated, its total linear momentum is conserved; that is,
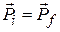 , (9-31)
, (9-31)
where the subscripts 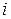 and
and 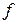 refer to values before and after the ejection, respectively. Because the motion is along a single axis, we can write momenta and velocities in terms of their
refer to values before and after the ejection, respectively. Because the motion is along a single axis, we can write momenta and velocities in terms of their  components. Before the ejection, we have
components. Before the ejection, we have
 (9-32)
(9-32)
Let 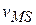 be the velocity of the ejected module relative to the Sun. The total linear momentum of the system after the ejection is then
be the velocity of the ejected module relative to the Sun. The total linear momentum of the system after the ejection is then
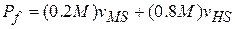 (9-33)
(9-33)
where the first term on the right is the linear momentum of the module and the second term is that of the hauler.
We do not know the velocity 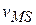 of the module relative to the Sun, but we can relate it to the known velocities with
of the module relative to the Sun, but we can relate it to the known velocities with
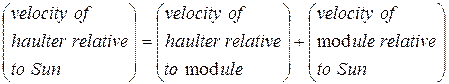
In symbols, this gives us
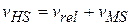
Or
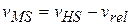
Substituting this expression for 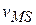 into Eq. 9-33, and then substituting Eqs. 9-32 and 9-33 into Eq. 9-31, we find
into Eq. 9-33, and then substituting Eqs. 9-32 and 9-33 into Eq. 9-31, we find
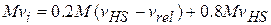
, which gives us
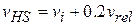 or
or
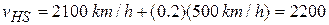 km/h. (Answer)
km/h. (Answer)
Sample Problem 9-7
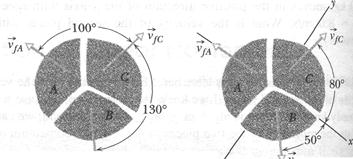
A firecracker placed inside a coconut of mass  , initially at rest on a frictionless floor, blows the coconut into three pieces that slide across the floor. An overhead view is shown in Fig. 9-10a. Piece C, with mass 0.30
, initially at rest on a frictionless floor, blows the coconut into three pieces that slide across the floor. An overhead view is shown in Fig. 9-10a. Piece C, with mass 0.30  , has final speed
, has final speed  = 5.0 m/s.
= 5.0 m/s.
(a) What is the speed of piece B, with mass 0.20  ?
?
|
SOLUTION: A Key Idea here is to see whether linear momentum is conserved. We note that (1) the coconut and its pieces form a closed system, (2) the explosion forces are internal to that system, and (3) no net external force acts on the system. Therefore, the linear momentum of the system is conserved.
To get started, we superimpose an xy coordinate system as shown in Fig. 9-l0b, with the negative direction of the x axis coinciding with the direction of  . The x axis is at 80░ with the
. The x axis is at 80░ with the 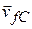 and 50░ with the direction of
and 50░ with the direction of 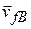 .
.
A second Key Idea is that linear momentum is conserved separately along -x and ˇ axes. Let's use the ˇ axis and write
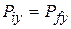
where subscript i refers to the initial value (before the explosion), and subscript ˇ refers to the ˇ component of 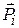 or
or 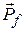 .
.
The component 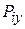 of the initial linear momentum is zero, because the coconut is initially at rest. To get an expression for
of the initial linear momentum is zero, because the coconut is initially at rest. To get an expression for  , we find the ˇ component of the final linear momentum of each
, we find the ˇ component of the final linear momentum of each
The Center of Mass
Physicists love to look at something complicated and find in it something simple and familiar. Here is an example. If you flip a baseball bat into the air, its motion as it turns is clearly more complicated than that of, say, a nonspinning tossed ball (Fig. 9-la), which moves like a particle.

|
Every part of the bat moves in a different way from every other part, so you cannot represent the bat as a tossed particle; instead, it is a system of particles.
However, if you look closely, you will find that one special point of the bat moves in a simple parabolic path, just as a particle would if tossed into the air (Fig. 9-lb). In fact, that special point moves as though (1) the bat's total mass were concentrated there and (2) the gravitational force on the bat acted only there. That special point is said to be the center of mass of the bat. In general:
► The center of mass of a body or a system of bodies is the point that moves as though all of the mass were concentrated there and all external forces were applied there.
The center of mass of a baseball bat lies along the bat's central axis. You can locate it by balancing the bat horizontally on an outstretched finger: The center of mass is on the bat's axis just above your finger.
9-2 The Center of Mass
We shall now spend some time determining how to find the center of mass in various systems. We start with a system of a few particles, and then we consider a system of a great many particles (as in a baseball bat).
Systems of Particles
Figure 9-2a shows two particles of masses 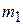 and
and 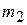 separated by a distance
separated by a distance  . We have arbitrarily chosen the origin of the x axis to coincide with the particle of mass
. We have arbitrarily chosen the origin of the x axis to coincide with the particle of mass 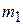 . We define the position of the center of mass (com) of this two-particle system to be
. We define the position of the center of mass (com) of this two-particle system to be
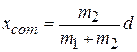 (9-1)
(9-1)
Suppose, as an example, that  . Then there is only one particle, of mass
. Then there is only one particle, of mass 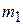 , and the center of mass must lie at the position of that particle; Eq. 9-1 dutifully reduces to
, and the center of mass must lie at the position of that particle; Eq. 9-1 dutifully reduces to 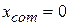 . If
. If  , there is again only one particle (of mass
, there is again only one particle (of mass 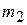 ), and we have, as we expect,
), and we have, as we expect, 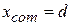 . If
. If 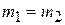 , the masses of the particles are equal and the center of mass should be halfway between them; Eq. 9-1 reduces to
, the masses of the particles are equal and the center of mass should be halfway between them; Eq. 9-1 reduces to 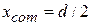 , again as we expect. Finally, Eq. 9-1 tells us that if neither
, again as we expect. Finally, Eq. 9-1 tells us that if neither 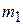 nor
nor 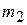 is zero,
is zero,  can have only values that lie between zero and
can have only values that lie between zero and  ; that is, the center of mass must lie somewhere between the two particles.
; that is, the center of mass must lie somewhere between the two particles.

Fig. 9-2 (a) Two particles of masses 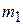 and
and 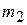 are separated by a distance
are separated by a distance  . The dot labeled com shows the position of the center of mass, calculated from Eq. 9-1. (b) The same as (a) except that the origin is located farther from the particles. The position of the center of mass is calculated from Eq. 9-2. The location of the center of mass (with respect to the particles) is the same in both cases.
. The dot labeled com shows the position of the center of mass, calculated from Eq. 9-1. (b) The same as (a) except that the origin is located farther from the particles. The position of the center of mass is calculated from Eq. 9-2. The location of the center of mass (with respect to the particles) is the same in both cases.
Figure 9-2b shows a more generalized situation, in which the coordinate system has been shifted leftward. The position of the center of mass is now defined as
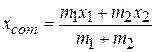 (9-2)
(9-2)
Note that if we put  , then
, then  becomes
becomes  and Eq. 9-2 reduces to Eq. 9-1, as it must. Note also that in spite of the shift of the coordinate system, the center of mass is still the same distance from each particle. We can rewrite Eq. 9-2 as
and Eq. 9-2 reduces to Eq. 9-1, as it must. Note also that in spite of the shift of the coordinate system, the center of mass is still the same distance from each particle. We can rewrite Eq. 9-2 as
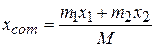 (9-3)
(9-3)
in which M is the total mass of the system. (Here,  .) We can extend this equation to a more general situation in which
.) We can extend this equation to a more general situation in which 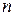 particles are strung out along the x axis. Then the total mass is
particles are strung out along the x axis. Then the total mass is 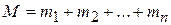 , and the location of the center of mass is
, and the location of the center of mass is
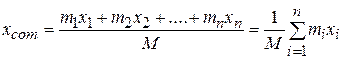 (9-4)
(9-4)
Here the subscript 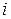 is a running number, or index, that takes on all integer values from 1 to n. It identifies the various particles, their masses, and their x coordinates. If the particles are distributed in three dimensions, the center of mass must be identified by three coordinates. By extension of Eq. 9-4, they are
is a running number, or index, that takes on all integer values from 1 to n. It identifies the various particles, their masses, and their x coordinates. If the particles are distributed in three dimensions, the center of mass must be identified by three coordinates. By extension of Eq. 9-4, they are
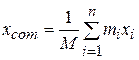 ,
, 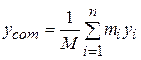
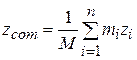 (9-j)
(9-j)
We can also define the center of mass with the language of vectors. First recall that the position of a particle at coordinates 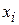 ,
, 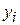 and
and  , is given by a position vector:
, is given by a position vector:
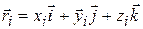 . (9-6)
. (9-6)
Here the index identifies the particle, and 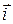 ,
, 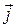 , and
, and  are unit vectors pointing, respectively, in the positive direction of the x, y, and z axes. Similarly, the position of the center of mass of a system of particles is given by a position vector:
are unit vectors pointing, respectively, in the positive direction of the x, y, and z axes. Similarly, the position of the center of mass of a system of particles is given by a position vector:
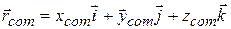 . (9-7)
. (9-7)
The three scalar equations of Eq. 9-5 can now be replaced by a single vector equation,
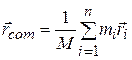 . (9-8)
. (9-8)
where again M is the total mass of the system. You can check that this equation is correct by substituting Eqs. 9-6 and 9-7 into it, and then separating out the x, y, and z components. The scalar relations of Eq. 9-5 result.
Solid Bodies
An ordinary object, such as a baseball bat, contains so many particles (atoms) that we can best treat it as a continuous distribution of matter. The "particles" then become differential mass elements dm, the sums of Eq. 9-5 become integrals, and the coordinates of the center of mass are defined as
 ,
,  ,
,  (9-9)
(9-9)
where  is now the mass of the object.
is now the mass of the object.
Evaluating these integrals for most common objects (like a television set or a moose) would be difficult, so here we shall consider only uniform objects. Such an object has uniform density, or mass per unit volume; that is, the density p (Greek letter rho) is the same for any given element of the object as for the whole object: 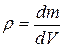 (9-10)
(9-10)
where dV is the volume occupied by a mass element 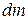 , and V is the total volume of the object. If we substitute
, and V is the total volume of the object. If we substitute 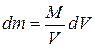 from Eq. 9-10 into Eq. 9-9, we find that
from Eq. 9-10 into Eq. 9-9, we find that
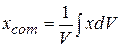 ,
, 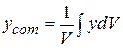 ,
, 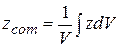
You can bypass one or more of these integrals if an object has a point, a line, or a plane of symmetry. The center of mass of such an object then lies at that point, on that line, or in that plane. For example, the center of mass of a uniform sphere (which has a point of symmetry) is at the center of the sphere (which is the point of symmetry). The center of mass of a uniform cone (whose axis is a line of symmetry) lies on the axis of the cone. The center of mass of a banana (which has a plane of symmetry that splits it into two equal parts) lies somewhere in that plane.
The center of mass of an object need not lie within the object. There is no dough at the center of mass of a doughnut, and no iron at the center of mass of a horseshoe.
|
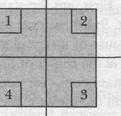
Checkpoint i: The figure shows a uniform square
plate from which four identical squares at the corners will be removed, (a) Where is the center of mass of the plate originally? Where is it after the removal of (b) square 1; (c) squares 1 and 2; (d) squares 1 and 3; (e) squares 1, 2, and 3; (f) all four squares? Answer in terms of quadrants, axes, or points (without calculation, of course).
Sample Problem 9-1
Three particles of masses 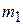 = 1.2 kg,
= 1.2 kg, 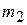 = 2.5 kg, and
= 2.5 kg, and 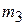 = 3.4 kg form an equilateral triangle of edge length a = 140 cm. Where is the center of mass of this three-particle system?
= 3.4 kg form an equilateral triangle of edge length a = 140 cm. Where is the center of mass of this three-particle system?

|
SOLUTION: A Key Idea to get us started is that we are dealing with particles instead of an extended solid body, so we can use Eq. 9-5 to locate their center of mass. The particles are in the plane of the equilateral triangle, so We need only the first two equations. A second Key Idea is that we can simplify the calculations by choosing the .rand ˇ axes so that one of the particles is located at the origin
and the x axis coincides with one of the triangle's sides (Fig. 9-3). The three particles then have the following coordinates:
| Particle | Mass (kg) | x (cm) | Ë (cm) |
| 1.2 | |||
| 2.5 | |||
| 3.4 |
The total mass M of the system is 7.1 kg.
From Eq. 9-5, the coordinates of the center of mass are

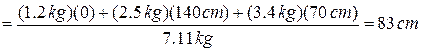 ;
;

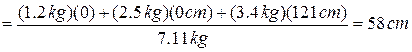
Sample Problem 9-2
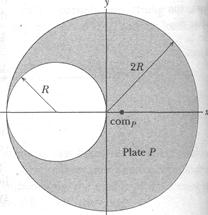
Figure 9-4a shows a uniform metal plate P of radius 2R from which a disk of radius R has been stamped out (removed) in an assembly line. Using the xy coordinate system shown, locate the center of mass comP of the plate.
SOLUTION: First, let us roughly locate the center of plate P by using the Key Idea of symmetry. We note that the plate is symmetric about the  axis (we get the portion below that axis by rotating the upper portion about the axis). Thus, comP must be on the
axis (we get the portion below that axis by rotating the upper portion about the axis). Thus, comP must be on the  axis. The plate (with the disk removed) is not symmetric about the
axis. The plate (with the disk removed) is not symmetric about the 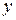 axis. However, because there is somewhat more mass on the right of the
axis. However, because there is somewhat more mass on the right of the 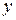 axis, comP must be somewhat to the right of that axis. Thus, the location of comP should be roughly as indicated in Fig. 9-4a.
axis, comP must be somewhat to the right of that axis. Thus, the location of comP should be roughly as indicated in Fig. 9-4a.
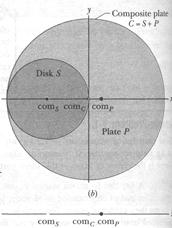
Another Key Idea here is that plate P is an extended solid body, so we can use Eqs. 9-11 to find the actual coordinates of comP. However, that procedure is difficult. A much easier way is to use this Key Idea: In working with centers of mass, we can assume that the mass of a uniform object is concentrated in a particle at the object's center of mass. Here is how we do so:
First, put the stamped-out disk (call it disk S) back into place (Fig. 9-4b) to form the original composite plate (call it plate C). Because of its circular symmetry, the center of mass comS for disk S is at the center of S, at 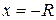 (as shown). Similarly, the center of mass comc for composite plate Đ is at the center of C, at the origin (as shown). We then have the following:
(as shown). Similarly, the center of mass comc for composite plate Đ is at the center of C, at the origin (as shown). We then have the following:
| Center | Location | |||
| Plate | of Mass | of com | Mass | |
| P | comf | xP = ? | mP | |
| S | coms | xs= -R | ms | |
| Đ | comc | xc = 0 | mc | ms + mP |
|
Now we use the Key Idea of concentrated mass: Assume that mass ms of disk S is concentrated in a particle at 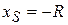 , and mass mP is concentrated in a particle at xP (Fig. 9-4c). Next treat these two particles as a two-particle system, using Eq. 9-2 to find their center of mass xs+P. We get
, and mass mP is concentrated in a particle at xP (Fig. 9-4c). Next treat these two particles as a two-particle system, using Eq. 9-2 to find their center of mass xs+P. We get
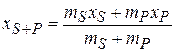 (9-12)
(9-12)
Next note that the combination of disk S and plate P is composite plate Đ Thus, the position xs+P of comS+P must coincide with the position xc of comc, which is at the origin; so xs+P = xc = 0. Substituting this into Eq. 9-12 and solving for xP, we get
|
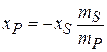 (9-13)
(9-13)
Now we seem to have a problem, because we do not know the masses in Eq. 9-13. However, we can relate the masses to the face areas of S and P by noting that
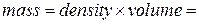
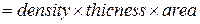
Then
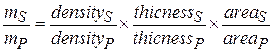
Because the plate is uniform, the densities and thicknesses are equal; we are left with
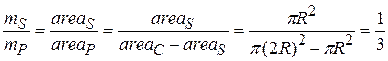
Substituting this and 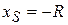 into Eq. 9-13, we have
into Eq. 9-13, we have
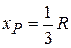
PROBLEM-SOLVING TACTICS
Date: 2015-01-12; view: 3800
| <== previous page | | | next page ==> |
| GRAVITATIONAL FIELD | | | Center-of-Mass Problems |