MASS AND WEIGHT

In the introductory discussion of force in Section 4—1 we mentioned that the weight of a body on earth, a familiar kind of force, is the result of the gravitational interaction of the body with the earth. We will study gravitational interactions in detail in Chapter 6, but some preliminary analysis is appropriate at this point. The terms mass and weight are often misused and interchanged in everyday conversation, and it is absolutely essential for us to keep clearly in mind the distinctions between these two physical quantities.

Mass, on the one hand, characterizes the inertial properties of a body. The greater the mass, the greater the force needed to produce a given acceleration; this meaning is reflected in Newton's second law, . Weight, on the other hand, is a force, exerted on a body by the earth or some other large body. Of course, everyday experience shows us that bodies having large mass also have large weight; a cart loaded with bricks is hard to get rolling because of its large mass, and it is also hard to lift off the ground because of its large weight. Thus we are led to ask what the relationship is between mass and weight. The answer to this question, according to legend, came to Newton as he sat under an apple tree watching the apples fall. A falling body has an acceleration, and according to Newton's second law this requires a force. If a 1-kg body falls with an acceleration of 9.80 m/s², the force required to cause this acceleration is

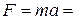(1 kg)(9.8 m/s²) = 9.8 kg m/s²= 9.8 N.

But the force that makes the body accelerate downward is its weight. Hence any body having a mass of 1 kg must have a weight of 9.8 N. We can generalize this result. ^/Denoting the weight of the body by 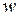, we say that a body having a mass 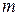must have a weight 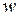given by

.

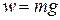The value of varies somewhat from point to point on the earth's surface. Part of this variation results from the fact that the earth's density is not uniform because of local deposits of ore, oil, or other materials of anomalous density. In addition, the earth is not perfectly spherical but is flattened at the poles and is slightly egg shaped. There are also complications associated with the rotation of the earth.

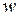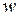As mentioned above, the weight of a standard kilogram at a point where = 9.80 m/s² is = 9.80 N. At a second point where = 9.78 m/s², the weight is = 9.78 N. Thus, unlike the mass of a body, which is constant, the weight of a body varies from one location to another. If we take a standard kilogram to the moon, where the acceleration of free fall is 1.67 m/s², its weight is 1.67 N but its mass is still 1 kg.

Because acceleration and force are both vector quantities, Eq. (4—9) may be written as a vector equation:

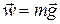
It is important to understand that the weight of a body, as given by Eq. (4-10), acts on the body all the time, whether it is actually in free fall or not. When a 1-kg body hangs suspended from a string, it is in equilibrium, and its acceleration is zero. But its weight is still acting on it and is given by Eq. (4—10). In this case there is also an upward force on the body provided by the string; the vector sum of the forces is zero, and the body is in equilibrium.

The mass of a body can be measured in several different ways. One way is to use the relationship 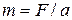. We apply a known force to the body, measure its acceleration, and compute the mass as the ratio of force to acceleration. This method, or some variation of it, is often used to measure the masses of atomic and subatomic particles.

Another method is to use a comparison technique, finding by trial some other body whose mass is equal to that of the given body but is already known. Often it is easier to compare weights than masses. The weight of a body equals the product of its mass and the acceleration of gravity, so if the weights of two bodies are equal at a given location, their masses are also equal. Balances can be used to determine with great precision (up to 1 part in 10⁶) when the weights of two bodies are equal, and hence when their masses are equal.

Thus mass plays two rather different roles in mechanics. On the one hand, the gravitational force acting on a body is proportional to its mass, so mass is the property of matter that causes bodies to exert attractive gravitational forces on each other. We may call this property gravitational mass. On the other hand, Newton’s second law tells us that the force (which need not be gravitational) required to cause an acceleration of a body is proportional to its mass. This inertial property of the body may be called its inertial mass.

It is not obvious that the gravitational mass of a particle has to be the same as its inertial mass, but very precise experiments have established (within about 1 part in 10 ) that in fact the two are the same. That is, if we have to push twice as hard on body A as on body В to cause a given acceleration, then the weight of A at a given location is precisely twice that of body В at the same location. Thus inertial and gravitational masses really are identical, and do not have to distinguish between them. This equivalence is also the fundamental reason why the acceleration of free fall is independent of mass.

Finally, we remark that the SI units for mass and weight are frequently misused in everyday speech. Expressions such as "This box weighs 6 kg" are nearly universal. What is meant, of course, is that the mass of the box (probably determined indirectly by weighing) is 6 kg. This usage is so common that there is probably no hope of straightening things out, but it is essential to recognize that the term weight is often used when mass is meant.

EXAMPLE 4—5 A flowerpot having a mass of 10 kg is suspended by a chain from the ceiling. What is its weight? What force (magnitude and direction) does the chain exert on it? What is the tension in the chain? Assume the weight of the chain itself is negligible.

Solution. Free-body diagrams for the flowerpot and the chain are shown in Fig. 4-12. The weight of the pot is given by Eq. (4-9):

= (10kg)(9.8m/s²) = 98 N.

The pot is in equilibrium, so the vector sum of forces acting on it must be zero. Thus the chain must pull up with a force of magnitude 98 N. By Newton's third law, the pot pulls down on the chain with a force of 98 N. Because the chain is also in equilibrium, there must be an upward force of 98 N exerted on the chain at its top end to make the vector sum of forces on the chain equal zero.

Example Weighing a Fish in an Elevator

A person weighs a fish of mass 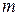on a spring scale attached to the ceiling of an elevator, as illustrated in Figure 5.14. Show that if the elevator accelerates either upward or downward, the spring scale gives a reading that is different from the weight of the fish.

Solution The external forces acting on the fish are the downward force of gravity and the force exerted by the scale. By Newton's third law, the tension is also the reading of the scale. If the elevator is either at rest or moving at constant velocity, the fish is not accelerating, and so 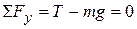or 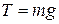(remember that the scalar 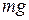is the weight of the fish).

If the elevator moves upward with an acceleration 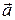relative to an observer standing outside the elevator in an inertial frame (see Fig. 5.14a), Newton's second law applied to the fish gives the net force on the fish:

(1) ,

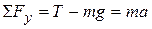where we have chosen upward as the positive direction. Thus, we conclude from (1) that the scale reading is greater than the weight 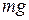if a is upward, so that 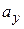is positive, and that the reading is less than 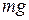if a is downward, so that 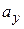is negative.

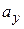For example, if the weight of the fish is 40.0 N and is upward, so that = +2.00 m/s², the scale reading from (1) is

(2) N.

If a is downward so that 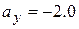m/s², then (2) gives us

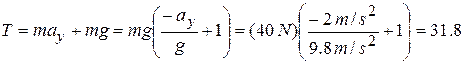N.

(a)

Figure 5.14 Apparent weight versus true weight, (a) When the elevator accelerates upward, the spring scale reads a value greater than the weight of the fish, (b) When the elevator accelerates downward, the spring scale reads a value less than the weight of the fish.

Hence, if you buy a fish by weight in an elevator, make sure the fish is weighed while the elevator is either at rest or accelerating downward! Furthermore, note that from the information given here one cannot determine the direction of motion of the elevator.

Special Cases. If the elevator cable breaks, the elevator falls freely and 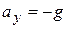. We see from (2) that the scale reading is zero in this case; that is, the fish appears to be weightless. If the elevator accelerates downward with an acceleration greater than g, the fish (along with the person in the elevator) eventually hits the ceiling because the acceleration of fish and person is still that of a freely falling object relative to an outside observer.

Date: 2015-01-12; view: 1690