Velocity and Coordinate by Integration

When varies with time, we can use the relation 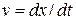to find the velocity as a function of time if the position is a given function of time. Similarly, we can use 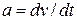to find the acceleration 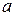as a function of time if the velocity 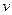is a given function of time.

We can also reverse this process. Suppose is known as a function of time; how can we find as a function of time? To answer this question, we first

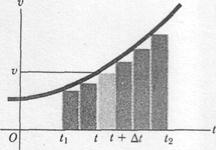Fig.3 The area under a velocity-time graph equals the displacement

consider a graphical approach. Figure 3 shows a velocity-versus-time curve for a situation where the acceleration (the slope of the curve) is not constant but increases with time. Considering the motion during the interval between times 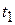and 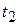, we divide this total interval into many smaller intervals, calling a typical one 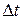. Let the velocity during that interval be . Of course, the velocity changes during 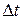, but if the interval is very small, the change will also be very small. This displacement during that interval, neglecting the variation of , is given by

.

This corresponds graphically to the area of the shaded strip with height and width 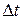, that is, the area under the curve corresponding to the interval 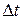. Since the total displacement in any interval (say, 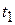to 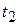) is the sum of the displacements in the small subintervals, the total displacement is given graphically by the total area under the curve between the vertical lines 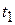and 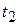. 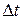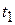In the limit, when all the become very small and their number very large, this is simply the integral of (which is in general a function of ) from and 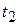. Thus is the position at time 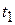and the position at time :

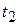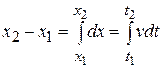(2-14)

A similar analysis with the acceleration-versus-time curve, where 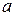is in general a function of , shows that if is the velocity at time 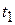and 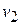the velocity at time 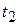, the change in velocity during a small time interval 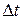is approximately equal to 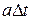, and the total change in velocity ( 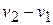) during the interval is given by

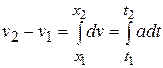
Or, finally, .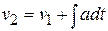

Exercises

1. Velocity of a body, moving in viscous medium, is given by the equation , where 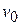- initial velocity, 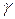- constant. What are the distance and acceleration as function of time?

2. A particle moves along a straight line with velocity 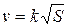, where 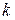is constant. If at time 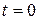the distance, traveled the particle was 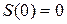, determine: (a) dependence of speed and acceleration on time ( and )

3. (a) If particle’s acceleration is given by 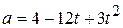, (where 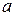is in meter/second² and in seconds), what its velocity at 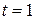? (b) What is its coordinate at 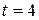s?

Date: 2015-01-12; view: 1394