Multiplexer Trees

A 2ⁿ-input multiplexer can be implemented by a two-level network of 2^n/2-input multiplexer modules as shown in Figure 1.41. The first level has 2^n/2 multiplex­ers, and n/2 of the select inputs are used to select a group of 2^n/2 from the 2ⁿ data inputs (one per multiplexer module). The second level uses the other n/2 select inputs to select one data input from the group already selected in the first level.

A high-level description of the network is as follows. The select input s is decomposed into two parts s_L and s_R so that

s = s_L · 2^n/2 + s_R

The vector s_R is applied to the first level and the vector s_L to the second. Consequently, the outputs of the first level are

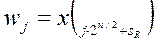j = 0, 1, … , 2^n/2 - 1

and the output of the whole multiplexer is

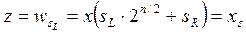
Fig. 1.41 - Multiplexer tree.

The enable input E is applied to the multiplexer in the second level. A functional description of a two-level multiplexer tree is

where x is divided into n/2 subvectors of n/2 bits each, so that

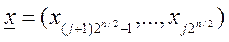
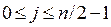
(Remember that the three arguments of the MUX function are the data vector, the select vector, and the enable input.)

The network shown in Figure 1.42 implements a 16-input multiplexer because

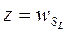and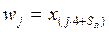

where

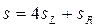
The multiplexer-tree scheme can be generalized to the case in which there are r levels. If n=rk, the network uses (2ⁿ-1)/(2^k-1) modules. This result is derived in a fashion similar to that for decoder trees.

Demultiplexer Networks

Since a demultiplexer is a decoder with a data input, a large demultiplexer can be implemented in the same ways as large decoders.

Encoder Networks

A 2ⁿ-input encoder can be implemented by a network of 2^k-input encoders and some other modules. We assume in the following discussion that n = 2k.

Fig. 1.42 - 16-input multiplexor implementation.

Date: 2015-01-12; view: 1877