High-Luminance Color Appearance Model

High dynamic range imaging systems (HDR) have become more widely used. Evaluation of HDR-systems colorimetry is a complex task as the existing color appearance models are based on relatively low-luminance experimental data. For instance, the LUTCHI color appearance data were obtained for luminances up to 690 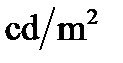(except the small amount of data obtained at 1000 and 1280 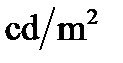). CIECAM02 color appearance model specifically was developed based on this data and it is not intended to operate in high-luminance domain. In addition, the majority of tone-mapping operators (the transforms necessary for perceptually correct reproduction of HDR-content on low-dynamic range displays) compress luminance range only, without dealing with the colorimetric parameters of images, thus resulting the colorimetric distortions. Thus there’s necessity to create universal color appearance model that can be applied to high-luminance stimuli. The [4.11] is devoted to one of the such kind of models. As the model is still under development, and its formulation in [4.11] has some ambiguities, we give its description with introductory aim. The testing of this model [4.11] has shown that the accuracy of its predictions at low and average luminance levels is close to CIECAM02 (it’s not surprising as this model was created based on CIECAM02 and partially on LUTCHI data); and at high luminance levels (up to 16680 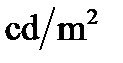) its performance exceeds CIECAM02.

The model consists of three main components: chromatic adaptation, cone responses, and cortex responses for each perceptual color attributes. It aims to accurately predict lightness, colorfulness and hue, including the Hunt effect, the Stevens effect, and simultaneous contrast. Additional correlates of brightness, chroma, and saturation will be derived as well.

As the focus of experiments [4.11] was not on chromatic adaptation, CIECAT02 chromatic adaptation transform [4.2] that has been shown to work well was adopted.

To evaluate cone responses Tristimulus values are first transformed into LMS cone space using the Hunt-Pointer-Estévez (HPE) transform [4.2, 4.4]. The cones’ absolute responses are modeled as following:

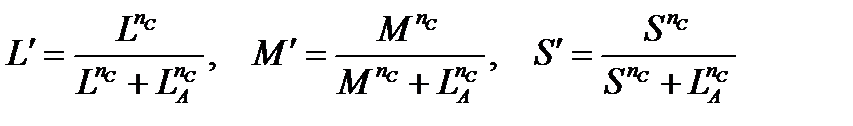(4.83)

where 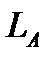is adaptation level value in 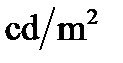. The adaptation level should ideally be the average luminance of the 10° viewing field. The parameter 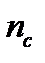is derived experimentally, .

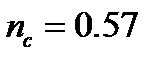The cone response then is converted into an achromatic signal A by averaging the contribution of each type of cone:

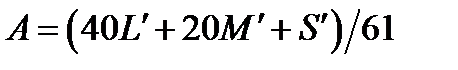(4.84)

The lightness is derived by:

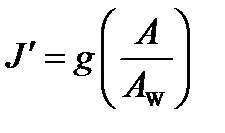(4.85)

with

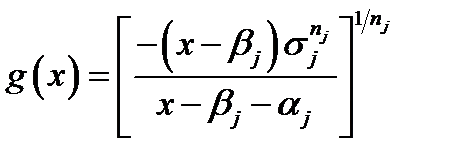(4.86)

The values of the parameters are derived from experimental data, yielding 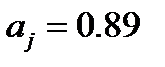, , 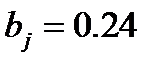, 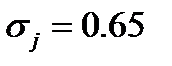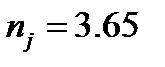. It is interesting to note that 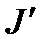may yield values below zero, in which case it should be clamped. This corresponds to the case where the observer cannot distinguish dark colors from even darker colors anymore.

As the perceived lightness values vary significantly with different media, the media-dependent lightness value is expressed as:

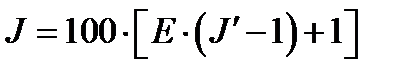(4.87)

where the parameter E is different for each medium. A value of 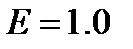corresponds to a high-luminance LCD display, transparent advertising media yield 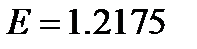, CRT displays are 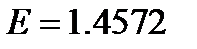, and reflective paper is 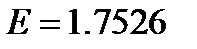. These parameters were derived from the LUTCHI data set.

The brightness is defined as:

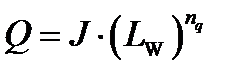(4.88)

The parameter 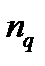is derived from experimental data,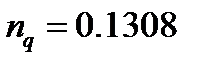

Preliminary red-green and yellow-blue opponent dimensions are calculated using:

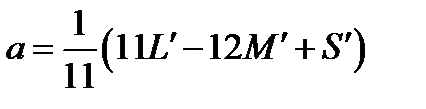(4.89)

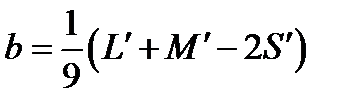(4.91)

Chroma is calculated as:

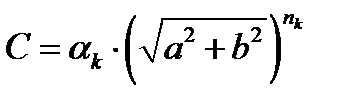(4.90)

where , ,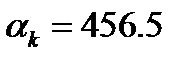

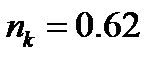Colorfulness is defined as:

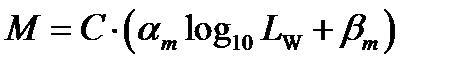(4.91)

where 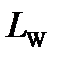is reference white luminance, ,

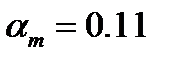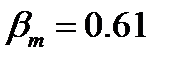
The other remaining quantity is saturation, which by definition is the colorfulness relative to its own brightness:

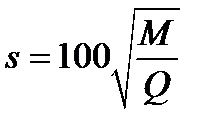(4.92)

The hue angle is computed by:

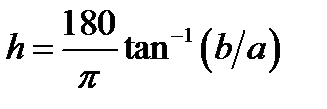(4.93)

Inverse model computation:

1. Compute achromatic white point 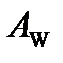of the target device using equations 4.82 and 4.83.

2. Compute brightness Q from lightness J:

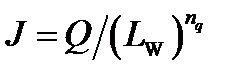(4.94)

3. Compute achromatic signal A from lightness J

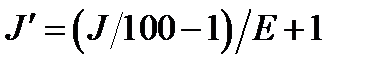(4.95)

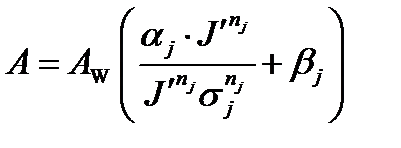(4.96)

4. Compute chroma C from colorfulness M

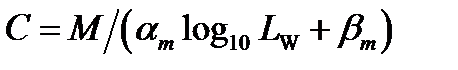(4.97)

5. Compute color opponents a & b from chroma C and hue h

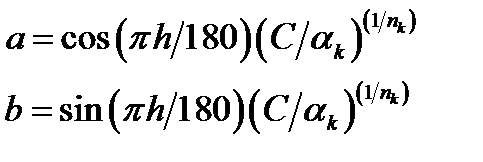(4.98)

6. Compute cone signals LMS from the achromatic signal A and opponents a & b

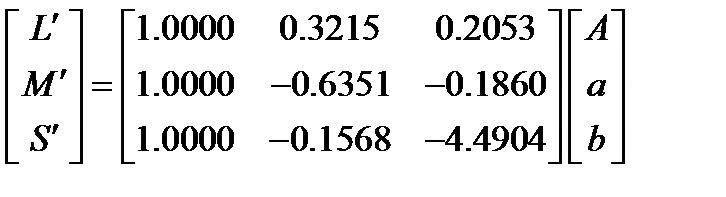(4.99)

7. Compute cone signals LMS from nonlinear cone signals

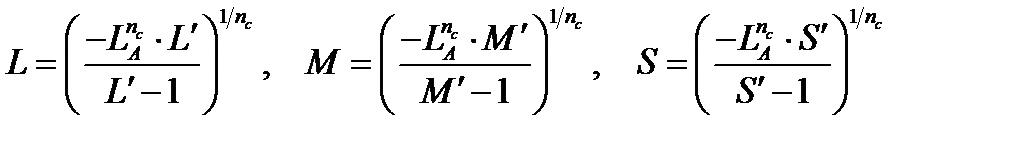(4.100)

8. Compute tristimulus 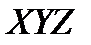from cone signals LMS using the HPE transform.

Apply inverse CIECAT02 transform (using target white).

Date: 2014-12-22; view: 1540