
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
ROTATION OF THE CELESTIAL SPHERE AT VARIOUS GEOGRAPHIC LATITUDES
I. As the Earth¢s surface is of the spherical form then the appearance of the star sky will depend on geographic latitude of observer¢s location. Depending on geographic latitude of location the diurnal circles of stars appear at different angles relative to the horizon.
To the observer on the North Pole of the Earth only a northern half of the celestial sphere is visible while on the South Pole only the southern half of the celestial sphere is visible. At the Earth¢s poles the celestial axis is directly overhead. The diurnal circles of stars are horizontal, i.e. all stars don't set and don't rise (stars are circumpolar) (fig. 129).
The appearance of the star sky changes as the observer moves from the North Pole towards the equator. The angular distance of the celestial North Pole gradually increases from a zenith. Therefore the diurnal circles of stars are tilted with respect to the horizon. At the same time the angle between the planes of the celestial equator and the celestial horizon increases and the stars located near the celestial equator will rise and set. When the observer is on the equator of the Earth the celestial pole will appear on the horizon line (directly in North and South points) and the celestial equator will pass through a zenith. The picture of movement of stars will have an appearance shown in fig. 130. The observer on the equator can see almost all stars of both hemispheres of the star sky.
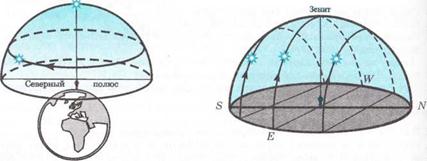
Fig. 129 Fig.130
II. The culminations of a star are the highest and lowest positions of the star with respect to the horizon reached when it crosses a celestial meridian. These positions are called the upper and lower culminations respectively.
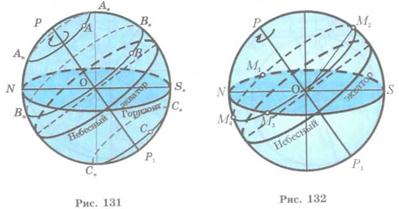
In fig. 131 the trajectories of diurnal motion of the stars visible at middle latitude are shown. Apparently, the star A is circumpolar and both of its culminations the upper (Au) and lower (Al) are above the horizon; and for the setting star B only the upper culmination is above the horizon (Bu). The star C at this location doesn't rise. Its upper and lower culminations are under the horizon.
III. Change of horizontal coordinates in a diurnal motion of stars. For the observer at middle latitudes the rise of a star occurs at certain time in the East of the horizon at point M1 (fig. 132). At this moment its horizontal coordinates are: h = 0o, A =ÐSOM1. The celestial object while rising above the horizon crosses the celestial meridian at point M2 and reaches its the upper culmination where the azimuth of the celestial object is A = 0° and the altitude h = ÐSOM2. Then the altitude of the object decreases and at other time it sets in the western part of the horizon at point M3 where h = 0o, A = ÐSOM3. The celestial object at point M4 again crosses the celestial meridian and reaches its lower culmination where h = ÐNOM4, A=180°. The object then moves from the point of the lower culmination to the rising point and finishes the diurnal cycle.
Thus we established that horizontal coordinates of a star within a day continuously change.
IV. Determination of geographical coordinates (latitude) on the Earth surface. Determination of geographic latitude on the surface of Earth is based on that fact that altitude of the celestial Pole above the horizon is equal to the observer¢s geographic latitude. However the location of the celestial Pole in the sky is not marked.
As the Polaris is located near the North Pole it is possible to determine approximately the latitude of the location. For this reason it is enough to measure the altitude of the Polaris using the goniometric tools (a sextant or a theodolit) and take it as the approximate value of the observer¢s latitude.
Equality of the observer¢s geographic latitude j to the altitude h of the celestial Pole can be established visually by means of the scheme (fig. 133) on which the point O designates position of the observer and ÐAO1O= j is the geographic latitude of the location. The equator (AA1) is perpendicular to the Earth¢s axes and the line of the horizon (SN) is perpendicular to the vertical direction. The observer sees the celestial Pole in the OP direction, this direction is parallel to the Earth¢s axis and ÐPON = hp is the altitude of the celestial Pole. As the angles with mutually perpendicular sides are equal then ÐPON =ÐAO1O. Therefore ÐAO1O = hp or hp =j.
Thus, the altitude of the celestial Pole above the horizon is equal to the observer¢s geographic latitude.
The geographic latitude of the location can be determined not only by using the Polaris. It can be determined by measuring the altitude of a star at its upper culmination.
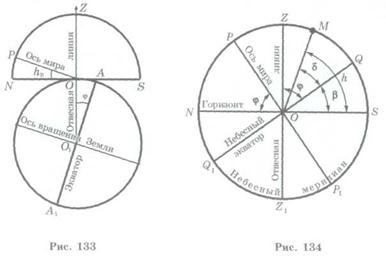
It is clear that the star at its culmination is located on the meridian. There is an elementary relationship between its declination (d), altitude (h) and geographic latitude of the observer (j) which can be established using fig. 134 where the star crosses its culmination point to the South from a zenith. We know that Ð PON = j is the altitude of the celestial Pole above the horizon. Figure 134 shows that Ð ZOQ =ÐPON (as angles with mutually perpendicular sides). The declination of a star (M) d = ÐMOQ, altitude h = d+b. Then, considering that 90° = b+ j, we get
h - d = 90o - j.
Hence, j = d + (90o - h). Here 90o – h = z is the zenith distance of the star. Therefore
j = d + z.
If the star¢s culmination point is to the North from a zenith, then
j = d - (90o - h) = d - z.
Hence, having measured the altitude of this or that star (h) at its upper culmination and knowing its declination (d), it is easy to determine the latitude of the observer¢s location.
Self-testing questions
1. Is it possible by the appearance of a rotating star sky to determine that the observer is on the Earth¢s North Pole?
2. How is the celestial equator located relative the horizon if the observer is on the terrestrial equator?
3. How much time in a day stars cross the celestial meridian?
4. Do a) Pole star; b) celestial poles; c) point of vernal equinox have their culmination point?
5. How is it possible to determine approximately the geographic latitude of the location by observing the Polaris (the Pole star)?
Exercise 32
1. Using the definition of the celestial object¢s culmination explain what are the rising, setting and circumpolar stars.
2. What is the altitude of Sirius at its upper culmination in Almaty (j = 43°15')?
3. The altitude of Altair at its upper culmination is 15°. Calculate the observer¢s geographic latitude if the declination of this star is +8o52'.
4. For the observer in Astana the star¢s altitude at its upper culmination is 40o18'. What is the declination of this star if the geographic latitude of Astana is 51o12'?
The experimental assignment
1. Find on the celestial map and sketch in a writing-book an appearance of the following constellations: the Great Bear, the Little Bear , the Cassiopeia, the Swan (Cygnus), the Lion (Leo), the Pegasus, the Boötes (the Herdsman) and the Orion.
2. Set on the MCM the date and time of your current lesson and determine what of the constellations listed in point 1 are above the horizon, what of them rise, set and what of them are at their culmination at present time.
3. Set on the MCM the time specified in the table of the day of observation and determine what of the constellations listed in the table, are located to the East, to the West, to the South and to the North from the Polaris (the Pole star). The obtained data write down in table 10. Determine the reason of the change of a visible appearance of the star sky.
Table 10
| Constellation | Position of the constellation at a certain time, t | |||
| Great Bear Cassiopeia Orion Swan (Cygnus) |
4. Using the MCM determine the time of rising, of the upper and lower culminations and of setting of the following stars: the Altair, the Sirius, the Pollux, the Rigel and the Antares on March 21 (on June 22, on September 23 and on December 22). Fill in the table 11.
Table 11
| Date | Star | Time, h,min | |||
| rise | upper culmination | set | lower culmination | ||
| 21.03 | Altair Sirius Pollux Rigel Antares |
Date: 2015-01-12; view: 4677
| <== previous page | | | next page ==> |
| MOBILE CELESTIAL MAP | | | LOCAL, ZONE AND universal TIME |