Examples of problem solving

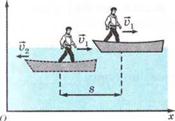
Example 1 The boat is in a state of rest on a pond. The boy with mass 40 kg standing in the boat walks from its bows to its stern. If the resistance of the water equals zero then what distance does the boat move relative to the water. The mass of the boat is 80 kg; its length is 3 m.

Information given

m₁ = 40 kg

m₂ = 80 kg

l = 3 m

--------------------

s -?

Solution Fig.72

The system “boy-boat” is not isolated as bodies of this system are acted on by external forces: the boy is acted on by the force of gravity and the boat is acted on by the force of gravity and buoyancy force. However these forces are vertically directed. There are no horizontal external forces acting on the bodies. Therefore the sum of x-components of momenta of the boy and the boat (fig. 72) remains constant and equals to zero as the boy and the boat were initially in a state of rest.

We attach the coordinate system to water. Let 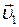to be the velocity of the boy relative to water; to be the velocity of the boat relative to water. Then the law of conservation of momentum gives:

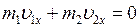(1)

Hence we have .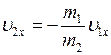

Since 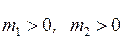then from the latter equation it follows that the velocity of the boat is opposite in direction to the velocity 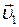of the boy. Taking this into account we get: 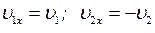. Then equation (1) is written as:

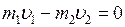. (2)

Let's denote the velocity of the boy relative to the boat by 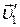, and the time needed for the boy to walk from boat’s bows to its stern by t. Then

(3)

where s is the distance covered by the boat during time interval t. Using vector addition we get:

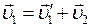
The x-component of this equation is 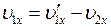or 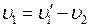and taking into account the expression (3) we rewrite the x-component as

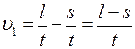
Substituting the expressions for 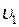and 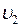into the equation (2) we obtain:

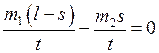
Hence 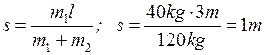. So, the boat covers the distance 1 m relative to water.

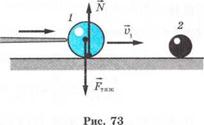
Example 2 A ball with mass 2 kg being hit with a billiard cue moves with a speed of 3 m/s and strikes the second ball with mass 1 kg that is in a state of rest. Determine the speed of balls after collision.

Information given

m₁ = 2 kg

m₂ = 1 kg

u = 3 m/s

--------------------

-? -?

Solution

The system of two balls is considered to be isolated as the force of gravity balances the support reaction force (fig.73). We ignore the friction force. In accordance with the law of conservation of momentum

(1)

where 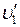and are speeds of the first and the second balls respectively after collision. The part of the kinetic energy of the first ball during collision is converted to the kinetic energy of the second ball hence we write the law of energy conservation:

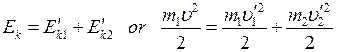(2)

We rewrite the equation (2) as

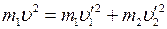(3)

Rearranging the expressions (1) and (2) we get the system of equations:

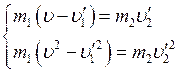
Now we divide the first equation of the system by the second equation to obtain

(4)

Substituting the expression (4) into the equation (1) we get

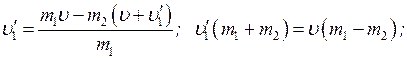
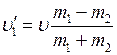(5)

Substituting the numerical values into equations (5) and (4) we find

.

Hence after elastic collision the balls move with speeds 1 m/s and 4 m/s respectively.

Example 3 The body with mass 250 g is thrown vertically up with a speed of 15 m/s. Find: 1) kinetic energy of the body at the starting instant; 2) potential energy of the body at the highest point of its path; 3) the maximum height of its path.

Information given

m = 250 g =0,25 kg

u = 15 m/s

g = 9,8 m/s²

--------------------

E_k -? E_p -?

h_max -?

Solution

At first we find kinetic energy of the body:

.

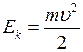The potential energy of the body at the highest point of its path is equal to its kinetic energy at the starting instant E_k = E_p .

;

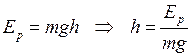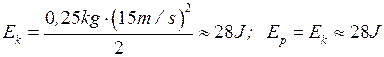
Now we calculate the maximum height of the body’s path:

Example 4 At the height of 50 m in the horizontal direction the body is tossed with an initial speed of 15 m/s. What is the speed of the body just before it hits the ground?

Information given

h = 50 m

u₀ = 15 m/s

g = 9,8 m/s²

--------------------

u -?

Solution

At the instant the body is tossed its total energy equals

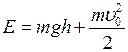
When the body hits the ground E_p = 0, then we get 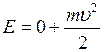. Hence

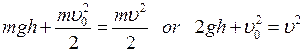
From the latter equation we find the target variable u

.

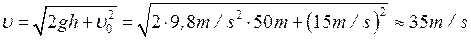Example 5 The spring with force constant 1000 N/m is stretched 6 cm from its unstretched length. What work is required to stretch this spring an additional 8 cm?

Information given

x₁ = 6 cm

Dx = 8 cm

k = 1000 N/m

--------------------

A -?

Solution

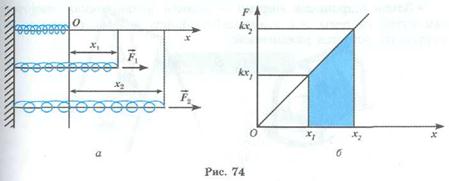
The first way to find work: let's denote by х₁ the initial elongation of the spring and by x₂ the elongation of the spring after stretching an additional distance Dh = 8 cm, i.e.

x₂ = x₁ + Dx =14 cm

We take the positive values of x in the direction of the stretching force and place the origin of the x-axis at the end of the unstretched spring (fig.74,a). Using Hooke’s law we write the expression for the x-component of the stretching force

F_x = kx or F = kx

The graph of force F as a function of x is shown in fig.74,b. The work done by this force to stretch the spring from x₁ to x₂ numerically is equal to the area of the shaded trapezoid:

.

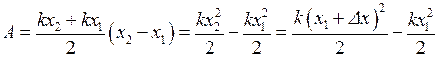The second way to find work: the work done to stretch the spring an additional distance equals the gain of its potential energy: A = E_p2 – E_p1 , where E_p1 and E_p2 are the potential energies of the spring at its elongations x₁ and x₂ = x₁ +Dx respectively. Hence,

.

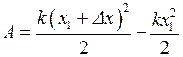Two ways to find the work give the same expression for the work. Substituting the numerical values of the given quantities into this expression we get A = 8 J.

SUMMARY OF THE CHAPTER III

· Momentum of a body is a vector quantity equal to the product of the body’s mass m and velocity : .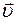

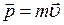· Conservation of momentum: the total momentum of the isolated system of bodies interacting with each other is constant or conserved

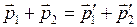
· Kinetic energy is the energy of a body in motion: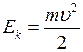

· Potential energy is the energy that depends on the position of interacting bodies relative each other:

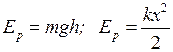
· Conservation of energy: the total mechanical energy of the isolated system of bodies that exert on each other by the force of gravity or elastic force is constant

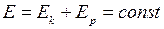
Date: 2015-01-12; view: 1215