The Nature of Algebra

Algebra is a generalization of arithmetic. Each statement of arithmetic has been dealing with particular numbers for years: the statement (20 + 4)² = 20² + 2 • 20 • 4 + 4² = 576 explains how the square of the sum of the two numbers, 20 and 4, may be computed. It can be shown that the same procedure applies if the numbers 20 and 4 are replaced by any two other numbers. In order to state the general rule, we write symbols, ordinary letters, instead of particular numbers. Let the number 20 be replaced by the symbol a, which may denote any number, and the number 4 by the symbol b. Then the statement is true that the square of the sum of any two numbers a and b can be computed by the rule (a + b)² = a² + 2a • b+b².

This is a general rule which remains true no matter what particular numbers may replace the symbols a and b. A rule of this kind is often called a formula.

Algebra is the system of rules concerning the operations with numbers. These rules can be most easily stated as formulas in terms of letters, like the rule given above for squaring the sum of two numbers.

The outstanding characteristic of algebra is the use of letters to represent numbers. Since the letters used represent numbers, all the laws of arithmetic hold for operations with letters.

In the same way, all the signs which have been introduced to denote relations between numbers and the operations with them are likewise used with letters.

For convenience the operation of multiplication is generally denoted by a dot as well as by placing the letters adjacent to each other. For example, a • b is written simply as ab.

The operations of addition, subtraction, multiplication, division, raising to a power and extracting roots are called algebraic expressions.

Algebraic expressions may be given a simpler form by combining similar terms. Two terms are called similar if they differ only in their numerical factor (called a coefficient).

Algebraic expressions consisting of more than one term are called multinomials. In particular, an expression of two terms is a binomial, an expression of three terms is a trinomial. In finding the product of multinomials we make use of the distributive law.

In algebra, the signs plus (+) and minus (-) have their ordinary meaning, indicating addition and subtraction and also serve to distinguish between opposite kinds of numbers, positive (+) and negative (-). In such an operation as + 10 – 10 = 0, the minus sign means that the minus 10 is combined with the plus 10 to give a zero result or that 10 is subtracted from 10 to give a zero remainder.

The so-called "double sign" (±), which is read "plus-or-minus", is sometimes used. It means that the number or symbol which it precedes may be "either plus or minus" or "both plus and minus".

As in arithmetic, the equality sign (=) means "equals" or "is equal to".

The multiplication sign (•) has the same meaning as in arithmetic. In many cases, however, it is omitted.

The division sign ( 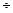) has the same meaning as in arithmetic. It is frequently replaced by the fraction line; thus 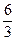means the same as 6 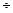3 and in both cases the result or quotient is 2. The two dots above and below the line in the division sign ( 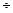) indicate the position of the numerator and the denominator in a fraction, or the dividend and the divisor in division.

Parentheses ( ), brackets [ ], braces { }, and other enclosing signs are used to indicate that everything between the two signs is to be treated as a single quantity.

Another sign which is sometimes useful is the sign which means "greater than" or "less than". The sign (>) means "greater than" and the sign (<) means "less than". Thus, a > b means that "a is greater than b", and 3<5 means "3 is less than 5".

Date: 2015-01-11; view: 2448