Local linear models

NATIONAL AVIATION UNIVERSITY

AEROSPACE CONTROL SYSTEMS INSTITUTE

DEPARTMENT OF AVIATION COMPUTER INTEGRATED COMPLEXES

ARTIFICIAL NEURAL NETWORKS

REPORT ON LAB:

RADIAL BASIS FUNCTION

done by _________________________

Group 307

Teacher: Sineglazov V.M.

Kyiv 2011

1. A radial basis function network is an artificial neural network that uses radial basis functions as activation functions. It is a linear combination of radial basis functions. They are used in function approximation, time series prediction, and control. Radial basis function neural networks are essentially a combination of the ideas found in multi-level perceptrons and those described earlier in this Guide under the main heading ?deterministic surface interpolation?, subsection ?radial basis functions?. In addition to interpolation they can be used for function approximation, as explained further below.

2. Network architecture:

o Normalized

o Local linear models

3. Network architecture: Radial basis function (RBF) networks typically have three layers: an input layer, a hidden layer with a non-linear RBF activation function and a linear output layer. The output, 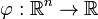, of the network is thus

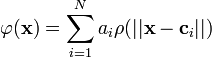
where N is the number of neurons in the hidden layer, is the center vector for neuron i, and a_i are the weights of the linear output neuron.

4.

Normalized architecture

In addition to the above unnormalized architecture, RBF networks can benormalized. Inthiscasethemappingis

where

is known as a "normalized radial basis function".

Local linear models

It is sometimes convenient to expand the architecture to include local linearmodels. Inthatcasethearchitecturesbecome, tofirstorder,

and

in the unnormalized and normalized cases, respectively. Here are weights to be determined. Higher order linear terms are also possible.

This result can be written

where

and

intheunnormalizedcaseand

in the normalized case.

Here δ_ij is a Kronecker delta function defined as

.

Examples

Logistic map

The basic properties of radial basis functions can be illustrated with a simple mathematical map, the logistic map, which maps the unit interval onto itself. It can be used to generate a convenient prototype data stream. The logistic map can be used to explore function approximation, time series prediction, and control theory. The map originated from the field ofpopulation dynamics and became the prototype for chaotic time series. Themap, inthefullychaoticregime, isgivenby

where t is a time index. The value of x at time t+1 is a parabolic function of x at time t. This equation represents the underlying geometry of the chaotic time series generated by the logistic map.

Generation of the time series from this equation is the forward problem. The examples here illustrate the inverse problem; identification of the underlying dynamics, or fundamental equation, of the logistic map from exemplars of the time series. Thegoalistofindanestimate

for f.

Date: 2016-06-12; view: 8