
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Example loop test case
| Parallel instruction tags | Instruction | Load/store instruction | Description |
| T | A | fadd fp3, fp1, fp0 | ; add FPR fp1 and fp0; store into target register fp3 |
| U | B | lfdu fp5, 8(r1) | ; load FPR fp5 from memory address: 8 + contents of GPR r1 |
| V | C | lfdu fp4, 8(r3) | ; load FPR fp4 from memory address: 8 + contents of GPR r3 |
| W | D | fadd fp4, fp5, fp4 | ; add FPR fp5 and fp4; store into target register fp4 |
| X | E | fadd fp1, fp4, fp3 | ; add FPR fp4 and fp3; store into target register fp1 |
| Y | F | stfdu fp1, 8(r2) | ; store FPR fp1 to memory address: 8 + contents of GPR r2 |
| Z | G | bc loop_yop | ; branch back conditionally to top of loop body |
The loop body consists of seven instructions labeled A through G. The final instruction is a conditional branch that causes control to loop back to the top of the loop body. Labels T through Z are used to tag the corresponding instructions for a parallel thread when considering SMT and CMP. The lfdu/stfdu instructions are load/store instructions with update where the base address register (say, r1, r2, or r3) is updated to hold the newly computed address. We assumed that the base machine is a four-wide superscalar processor with two load-store units supporting two floating-point pipes. The data cache has two load ports and a separate store port. The two load-store units (LSU0 and LSU1) are fed by a single issue queue LS0; similarly, the two floating-point units (FPU0 and FPU1) are fed by a single issue queue FPQ. In the context of the loop just shown, we essentially focus on the LSU-FPU subengine of the whole processor.
Assume that the following high-level parameters (latency and bandwidth) characterizing the base superscalar machine:
? Instruction fetch bandwidth fetch_bw of two times W is eight instructions per cycle.
? Dispatch/decode/rename bandwidth equals W, which is four instructions/cycle; dispatch stalls beyond the first branch scanned in the instruction fetch buffer.
? Issue bandwidth from LSQ (reservation station) lsu_bw of W/2 is two instructions/cycle.
? Issue bandwidth from FPQ fpu_bw of W/2 is two instructions/cycle.
? Completion bandwidth compl_bw of W is four instructions/cycle.
? Back-to-back dependent floating-point operation issue delay fp_delay is one cycle.
? The best-case load latency from fetch to write back is five cycles.
? The best-case store latency, from fetch to writing in the pending store queue is four cycles. (A store is eligible to complete the cycle after the address-data pair is valid in the store queue.)
? The best-case floating-point operation latency from fetch to write back is seven cycles (when the FPQ issue queue is bypassed because it's empty).
Load and floating-point operations are eligible for completion (retirement) the cycle after write back to rename buffers. For simplicity of analysis assume that the processor uses in-order issue from issue queues LSQ and FPQ. In our simulation model, superscalar width W is a ganged parameter, defined as follows:
? W= (fetch_bw/2) = disp_bw = compl_bw.
? The number of LSD units, Is_units, FPL units, fp_units, data cache load ports, I_ports, and data cache store ports, the term s_ports, vary as follows as W is changed: Is_units = fp_units = I_ports = max [floor(W/2), 1 ]. s_ports = max [floor(I_ports/2), 1 ].
We assumed a simple analytical energy model in which the power consumed is a function of parameters W, Is_units, fp_units, I_ports, and s_ports. In particular, the power (PW) in pseudowatts is computed as
PW = W 0.5 + Is_units + fp_units + I_ports + s_ports.
Fig. 6.10 shows the performance and performance/power ratio variation with superscalar width. The MIPS values are computed from the CPI values, assuming a 1-GHz clock frequency.
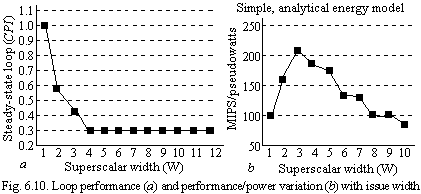 The graph in Fig. 6.10,a shows that a maximum issue width of four could be used to achieve the best (idealized) CPI performance. However as shown in Fig. 6.10,b, from a power-performance efficiency viewpoint (measured as a performance over power ratio in this example), the best-case design is achieved for a width of three. Depending on the sophistication and accuracy of the energy model (that is, how power varies with microarchitectural complexity) and the exact choice of the power-performance efficiency metric, the maximum value point in the curve in Fig. 6.10,b will change. However beyond a certain superscalar width, the power-performance efficiency will diminish continuously. Fundamentally, this is due to the single-thread ILP limit of the loop trace.
The graph in Fig. 6.10,a shows that a maximum issue width of four could be used to achieve the best (idealized) CPI performance. However as shown in Fig. 6.10,b, from a power-performance efficiency viewpoint (measured as a performance over power ratio in this example), the best-case design is achieved for a width of three. Depending on the sophistication and accuracy of the energy model (that is, how power varies with microarchitectural complexity) and the exact choice of the power-performance efficiency metric, the maximum value point in the curve in Fig. 6.10,b will change. However beyond a certain superscalar width, the power-performance efficiency will diminish continuously. Fundamentally, this is due to the single-thread ILP limit of the loop trace.
Note that the resource sizes (number of rename buffers, reorder buffer size, sizes of various other queues, caches, and so on) are assumed to be large enough that they're effectively infinite for the purposes of our running example. Some of the actual sizes assumed for the base case (W = 4) are
? completion (reorder) buffer size cbuf_size of 32,
? load-store queue size lsq_ of 6,
? floating-point queue fpqze of 8, and
? pending store queue size psq_size of 16.
The microarchitectural trends beyond the current superscalar regime are effectively targeted toward the goal of extending the processing efficiency factors. That is, the complexity growth must ideally scale at a slower rate than performance growth. Power consumption is one index of complexity; it also determines packaging and cooling costs. (Verification cost and effort is another important index.) In that sense, striving to ensure that the power-performance efficiency metric of choice is a nondecreasing function of time is a way of achieving complexity-effective designs.
In a multiscalar-type CMP machine, different iterations of a loop program could be initiated as separate tasks or threads on different core processors on the same chip. Thus in a two-way multiscalar CMP, a global task sequencer would issue threads A-B-C-D-E-F-G and T-U-V-W-X-Y-Z derived from the same user program in sequence to two cores.
Register values set in one task are forwarded in sequence to dependent instructions in subsequent tasks. For example, the register value in fp1 set by instruction E in task 1 must be communicated to instruction T in task 2. So instruction T must stall in the second processor until the value communication has occurred from task 1. Execution on each processor proceeds speculatively, assuming the absence of load-store address conflicts between tasks. Dynamic memory address disambiguation hardware is required to detect violations and restart task executions as needed. If the performance can be shown to scale well with the number of tasks, and if each processor is designed as a limited-issue, limited-speculation (low-complexity) core, we can achieve better overall scalability of power-performance efficiency.
Date: 2016-06-12; view: 327
| <== previous page | | | next page ==> |
| Microarchitecture Level Power-Performance Fundamentals | | | The Design Space of Register Renaming Techniques |