
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Problems for Self-Testing on Module I
1. Represent each of the decimal values 26,-37, 497, and -123 as signed 10-bit numbers in the following binary formats: (a) Sign and magnitude; (b) 1?s complement; (c) 2?s complement.
2. (a) Express the decimal values 0.5, -0.123, -0.75, and -0.1 as signed 6-bit numbers in the binary formats. (b) What is the maximum representation error e involved in using only 5 significant bits after the binary point?
(c) Calculate the number of bits needed after the binary point so that (1) e < 1/10, e < 1/100, (3) e < 1/1000, and (4) e < 1/106.
3. The 1's-complement and 2's-complement binary representation methods are special cases of the (b-1)'s-complement and b's-complement representation techniques in base b number systems. For example, consider the decimal system. The sign and magnitude values +527 and -382 have four-digit signed-number representations in each of the complement systems as shown in
| Table Q1.1 Signed numbers in base 10 | ||
| Representation | Two examples | |
| Sign and magnitude | +527 | -382 |
| 9's complement | ||
| 10's complement |
Table Q1.1. The 9's complement is formed by taking the complement of each digit position with respect to 9. The 10's complement is formed by adding 1 to the 9's complement. In each of the latter two representations, the leftmost digit is 0 for a positive number and 9 otherwise.
Now consider the base 3 (ternary) system, where the positive five-digit number t4t3t2t1t0 has the value t4 × 34 + t3 × 33 + t2 × 32 + t1 × 31 + t0 × 30, with 0 ≤ ti ≤ 2. Express the ternary sign and magnitude numbers +2120, -1212, +10, and -201 as five-digit signed ternary numbers in both the 2's-complement and 3's-complement systems.
4. Using the "paper-and-pencil" methods, perform the operations A×B and A÷B on the 5-bit positive numbers A = 10101 and B = 00101.
5. Consider the binary numbers in the following add and subtract problems to be signed 6-bit values in the 2's-complement representation. Perform the operations indicated, specify the cases where overflow occurs and where no overflow occurs, and check your answers by converting operands and results to decimal sign and magnitude representation.
| + 001001 | + 100101 | + 000111 | + 010000 | + 111001 | + 101011 |
| - 011111 | - 100101 | - 011101 | - 000111 | - 111000 | - 100010 |
6. Show how the multiplication and division operations in Question 5 would be performed by the hardware in Fig. 2.8.a (p. 62) and 2.22 (p. 72), respectively, by constructing the equivalent of Fig. 2.8.b (p. 62) and 2.24 (p. 74) for the above A and B operands.
7. Multiply the signed 6-bit numbers A = 010111 (multiplicand) and B = 110110 (multiplier) using the Booth algorithm.
8. Repeat Question 7 using bit pairing of the multiplier.
9. Construct the equivalent of Fig. 2.19 (p. 69) for the multiplication operation in Question 7.
10. Derive logic equations that specify the ADD/SUB and SR outputs of the combinational CONTROL network in Fig. 2.26 (p. 80).
11. In Section 2.5, we used a practical size 32-bit format for floating-point numbers. In this Question, we will use a shortened format that retains all the pertinent concepts but is manageable for working through numerical exercises.
 Consider that floating-point numbers are represented in a 12-bit format as follows:The scale factor has an implied base of 4, and a 5-bit, excess-16 exponent. The 6-bit mantissa is normalized.
Consider that floating-point numbers are represented in a 12-bit format as follows:The scale factor has an implied base of 4, and a 5-bit, excess-16 exponent. The 6-bit mantissa is normalized.
(a) What does ?normalized? mean in the context of this format?
(b) Represent the numbers +1.7, -0.012, +19, and 1/8 in this format.
(c) What is the range representable in this format?
(d) How does the range calculated in (c) compare to 12-bit integer or fraction ranges?
(e) Perform Add, Subtract, Multiply, and Divide operations on the operands:

12. Consider the representation of the decimal number 0.1 as a signed 8-bit binary fraction in the representation discussed in Section 2.5. If this number does not convert exactly in this 8-bit format, give the approximations to it that are developed by all three of the truncation methods discussed in Section ?Guard Bits and Rounding? (p. 78-79).
13. It is required to build a modulo 10 adder for adding BCD digits. Modulo 10 addition of two numbers A = A3A2A1A0 and B = B3B2B1B0 can be achieved in two stages: 1. Add A to B (binary addition). 2. If the result is an illegal code that is greater than or equal to 1010, add 610; otherwise, add 0. Ignore overflow from this stage of the adder.
(a) Show that the above algorithm will give correct results for:
(1) A = 0101 B = 0110; (2) A = 0011 B = 0100.
(b) Design a BCD digit adder using logic gates and the 4-bit MSI chip described in Section 2.2. The inputs are A3A2A1A0, B3B2B1B0, and a carry-in. The outputs are the sum digit S3S2S1S0 and the carry-out. A cascade of such blocks can form a ripple-carry BCD adder.
14. If gate fan-in limited to four, how can the hex digit SHIFTER in Fig. 2.26 (p. 80) be implemented combinationally?
15. (a) Sketch a logic-gate network that implements the multiplexer MPX in Fig. 2.26 (p. 80). (b) Relate the structure of the SWAP network in Fig. 2.26 (p. 80) to your solution to part (a).
16. How can the ?leading hex zeros detector? of Fig. 2.26 (p. 80) be implemented combinationally?
17. The Mantissa adder-subtractor in Fig. 2.26 (p. 80) operates on positive, unsigned binary fractions and must produce a sign and magnitude result. In the discussion accompanying Fig. 2.26 (p. 80), we stated that 1?s complement arithmetic is convenient because of the required format for input and output operands. When adding two signed numbers in 1?s-complement notation, the carry-out from the sign position must be added to the result to obtain the correct signed answer. This is called ?end-around carry? correction. Consider the following examples of addition using signed 4-bit encodings of operands and results in the 1?s-complement system:

1?s-complement arithmetic is convenient when a sign and magnitude result is to be generated because a negative number in 1?s-complement notation can be converted to sign and magnitude by complementing the bits to the right of the sign-bit position. Using 2?s-complement arithmetic, addition of +1 is needed for conversion of a negative value into sign and magnitude logic.
With the above discussion as a guideline, give the complete design of the 1?s-complement adder-subtractor in Fig. 2.26 (p. 80).
18. Give the complete design of the 4-bit ALU circuit block shown in Fig. 2.6,b (p. 59). Omit the control inputs and assume that the circuit performs only 4-bit addition. Carry lookahead logic is to be used for all the internal carries c1, c2, and c3 as well as for the block output c4.
Your answer can be in the form of a sketch of the logic-gate network required or a listing of logic equations that describe the network.
19. Four 4-bit adder circuits shown in Fig. 2.6,b (p. 59) can be cascaded to form a 16-bit adder. In this cascade, the output c4 from the low-order circuit is connected as the carry-in to the next circuit. Its carry-out, c8, is connected as the carry-in to the third circuit, etc.
(a) A faster adder can be constructed by using external logic to generate the carry-in variables for the three high-order circuits. Give the logic design for an integrated circuit ?carry lookahead? chip that has outputs c4, c8, and c12. Its inputs are c0, PI0, GI0, PI1, GI1, PI2, and GI2. Estimate the increase in adder speed achievable by using this circuit in conjunction with the four 4-bit adder circuits, as opposed to using a cascade of the adder circuits, in building a 16-bit adder.
(b) Extend your part (a) design by assuming that the carry lookahead chip has PI3 and GI3 as additional inputs and provides additional outputs PII0 and GII0. These higher-level propagate and generate functions are defined by
PII0 = PI3PI2PI1PI0
GII0 = GI3 + PI3GI2 + PI3PI2GI1 + PI3PI2PI1GI0
Note that this extended circuit requires 16 external pin connections, consisting of 14 for input and output variables and 2 for power connections, so that it can be accommodated in a standard 16-pin IC package.
(c) Design a 64-bit adder that uses sixteen 4-bit adder circuits, some carry lookahead circuits defined by the design from part (b), and some additional logic to generate c16, c32, and c48 from c0, and the PIIi and GIIi variables generated by the lookahead circuits. What is the relationship of the additional logic to the logic inside each lookahead circuit?
20. Fig. Q1.1 shows a two-dimensional array of combinational logic cells for 3 × 3 positive-number multiplication. Analyze the typical cells and data flow to verify that it computes products properly.
(a) Compare the total delay in developing the product in this type of array with that of Fig. 2.7 (p. 61) as a function of the input operand length n.
(b) Which of the cells in Fig. Q1.1 and its n × (n + 1) extension perform no useful function? This cellular logic arrangement is a basis for some of the 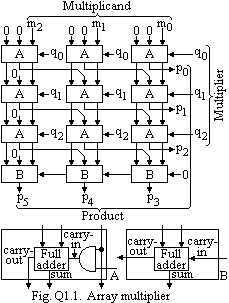 VLSI multiplier chips that are commercially available.
VLSI multiplier chips that are commercially available.
21. The array described in Question 20 is an example of the application of the principle of carry-save addition. This principle can be applied in any situation where a number of summands ne-ed to be added to generate a sum.
The simplest example is in the case of adding three numbers W, X, and Y. The straightforward way to do this is to add W to X and then add the resulting sum to Y to generate the answer. An alterna-tive, using carry-save addition, is to combine the three operands with n full adders to generate two numbers, S (sum bits) and C (carry bits), which are then added in a ripple-carry adder to generate the desired sum. This process is shown in Fig. Q1.2.

(a) Apply this idea to the multiplication of two n-bit positive numbers. Start by considering the problem as one of adding summands, appropriately shifted, as in the paper-and-pencil method. Reduce these n summands to 2/3 n numbers by performing carry-save additions on them in parallel in groups of three. Then reduce the results, etc., until only two numbers remain. They are finally added to generate the desired product. This principle is used in many high-performance computers.
(b) Compare the speed and cost of this type of multiplier with that of Question 20 or Fig. 2.7 (p. 61).
(c) Can bit grouping of the multiplier be combined with carry-save addition to configure a faster and/or cheaper multiplier?
22. (a) Multiply the signed 2's-complement 8-bit numbers A = 00011010 (Multiplicand) and B = 11000111 (Multiplier) using the Booth algorithm and generating a 16-bit product.
(b) Compute the sign and magnitude decimal representations of A, B, and the product from part (a).
23. Repeat problem 22 using bit pairing of the multiplier.
24. Consider a 16-bit floating-point number in a format similar to that of Question 11 with a 6-bit exponent and a 9-bit normalized fractional mantissa. The base of the scale factor is 8 and the exponent is represented in excess-32 format.
(a) Add the numbers A = 0 100001 111111110 and B = 0 011111 101010101 which are expressed in the above format, giving the answer in normalized form. Use rounding as the truncation method when producing the final normalized 9-bit mantissa.
(b) Using decimal numbers w, x, y, and z, express the magnitude of the largest and smallest (nonzero) values representable in the above normalized floating-point format, in the form: Largest = w × 8x, Smallest = y × 8-z.
25. Show how to modify the circuit diagram of Fig. 2.8 (p. 62) to implement multiplication of signed, 2's-complement, n-bit numbers using the Booth algorithm.
26. Suppose an ?Enable? input is added to an integrated circuit that performs the decoding function. When Enable = 0, all the outputs are held at 0; when Enable = 1, the circuit performs the decode function. This can be implemented internally by adding Enable as an input to each of the AND gates that generates the decoder outputs.
Show how to use two-input decoders that have Enable inputs to implement a single four-input decoder.
27. Give a block diagram, similar to Fig. 1.26 (p. 34), for a 256K × 16 memory using 64K × 1 memory chips.
Date: 2016-06-12; view: 336
| <== previous page | | | next page ==> |
| Floating-Point Numbers and Operations | | | CISC and RISC Microprocessors |