
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Computer Arithmetic
All operations in a digital computer are executed as sequences of elementary microoperations: receipt, transmission and delivery of operands; right or left shift of operands on the set number of digits (cyclic, arithmetic, logical, modified); addition to the operand of constant; comparison of operands; bits logical flipping (disjunction, conjunction, equivalentness, addition on the module 2); arithmetic addition of two operands proper to the numbers in the same number system; code conversion of operands (including an inversion, addition, coding, decoding). Under computer arithmetic we will understand the aggregate of principles and numerical information presentation forms, methods and algorithms of implementation of arithmetic operations and calculation of the elementary functions examined at the level of structural internals of hardwares of digital computer [45].
 Addition of Positive Numbers.We will be concerned only with positive numbers; hence, we will drop the sign-bit position from most of our discussions. Such numbers are called unsigned numbers. Consider adding two 1-bit numbers. The results are shown in Fig. 2.1. The sum of 1 and 1 requires the 2-bit vector 10 to represent the value 2. We say that the sum is 0 and the carry-out is 1. These examples extend to the addition of multibit vectors in an obvious way. The operation is analogous to the usual hand computation with decimal numbers. We add bit pairs starting from the low-order (right) end of the bit vectors, propagating carries toward the high-order (left) end. The truth table for the sum and carry-out functions for adding two equally weighted bits xi and yi in vectors X and Y is shown in Fig. 2.2. The figure also gives two-level AND-OR logic expressions for these functions, along with an example of addition. Note that each stage of the addition algorithm must be able to accommodate a carry-in bit. We shall use ci to represent the carry-in to the ith stage and the carry-out from the (i - 1)st stage.
Addition of Positive Numbers.We will be concerned only with positive numbers; hence, we will drop the sign-bit position from most of our discussions. Such numbers are called unsigned numbers. Consider adding two 1-bit numbers. The results are shown in Fig. 2.1. The sum of 1 and 1 requires the 2-bit vector 10 to represent the value 2. We say that the sum is 0 and the carry-out is 1. These examples extend to the addition of multibit vectors in an obvious way. The operation is analogous to the usual hand computation with decimal numbers. We add bit pairs starting from the low-order (right) end of the bit vectors, propagating carries toward the high-order (left) end. The truth table for the sum and carry-out functions for adding two equally weighted bits xi and yi in vectors X and Y is shown in Fig. 2.2. The figure also gives two-level AND-OR logic expressions for these functions, along with an example of addition. Note that each stage of the addition algorithm must be able to accommodate a carry-in bit. We shall use ci to represent the carry-in to the ith stage and the carry-out from the (i - 1)st stage.

 A combination logic implementation of the truth table for addition is shown in Fig. 2.3,a along with a convenient symbol to be used in the subsequent discussion. Other logic circuits can be used to realize these functions; for example, either NAND or NOR gates can be used. A cascaded connection of n ADDER blocks, as shown in Fig. 2.3,b, can be used to add two n-bit numbers. Since the carries propagate, or ripple, through this cascade, the configuration is called an n-bit ripple-carry adder. When the carry-out cn from the most significant bit (MSB) position is equal to 1, there is an overflow from the operation. This means that the result cannot be represented in an n-bit number. The carry-in c0 into the least significant bit (LSB) position is 0 for the addition of two positive numbers but may be 0 or 1 in more general situations. For instance, forming the 2's complement of a number involves add-ing 1 to the bit complement of the number. The input c0 can be conveniently used to perform the +1 part of the operation. This allows complementa-tion to be combined with addition. The convenience of that combination will become clearer in a later section on addition and subtraction of signed numbers in the 2's-complement representation [2], [4], [13], [16], [44], [47], [53].
A combination logic implementation of the truth table for addition is shown in Fig. 2.3,a along with a convenient symbol to be used in the subsequent discussion. Other logic circuits can be used to realize these functions; for example, either NAND or NOR gates can be used. A cascaded connection of n ADDER blocks, as shown in Fig. 2.3,b, can be used to add two n-bit numbers. Since the carries propagate, or ripple, through this cascade, the configuration is called an n-bit ripple-carry adder. When the carry-out cn from the most significant bit (MSB) position is equal to 1, there is an overflow from the operation. This means that the result cannot be represented in an n-bit number. The carry-in c0 into the least significant bit (LSB) position is 0 for the addition of two positive numbers but may be 0 or 1 in more general situations. For instance, forming the 2's complement of a number involves add-ing 1 to the bit complement of the number. The input c0 can be conveniently used to perform the +1 part of the operation. This allows complementa-tion to be combined with addition. The convenience of that combination will become clearer in a later section on addition and subtraction of signed numbers in the 2's-complement representation [2], [4], [13], [16], [44], [47], [53].
Fig. 2.3,c shows k n-bit adders cascaded to form an adder capable of handling input vectors of length kn bits. This schematic is representative of a number of different addition situations. In some instances, k logic hardware adders are involved. However, the figure is also representative of the use of one n-bit hardware adder that is serially reused by software means to perform k n-bit additions. The simplest case is that of full hardware addition of two kn-bit words in the ALU of a CPU. If n = k = 4, the picture could represent a 16-bit adder implemented by a cascade of four 4-bit MSI adder chips. For n = 32, the picture could represent a multiple-precision addition operation in a 32-bit word-length computer using a 32-bit hardware adder. The parameter k, then determines the precision. If k = 1, it is normal to say that a single-precision operation is being performed; if k = 2, double precision is being implemented. In this particular case, a single n-bit adder is used in a time sequence of k n-bit additions performed by software. The carry-out signal from each n-bit addition is stored in a flip-flop to be used as the carry-in signal to the next n-bit addition. This storage of the carry-out signal will also occur when implementing multiplication as a series of additions. We will present the details later.
This rather extended discussion of Fig. 2.3,c is intended to indicate that an n-bit adder with both carry-in (c0) and carry-out (cn) signals is an important building block in all arithmetic operations.
Logic Design for Fast Adders.The n-bit ripple-carry adder shown in Fig. 2.3,b may have too much delay in developing its outputs cn, sn-1, ?, s1, and s0. Whether the delay associated with any particular implementation technology is acceptable can be decided only in the context of the speed of other CPU components and the main memory cycle time. Delay through a network of logic gates is clearly dependent on the electronic technology used in fabricating the basic gates and the number of gates in the paths from inputs to outputs. After a particular technology (often called a logic family) is specified, the delay associated with any combinational logic network constructed from gates in that technology can be determined by adding up the number of logic-gate delays along the longest path through the network. In the case of the ripple-carry adder, the longest signal propagation is clearly from the inputs x0, y0, c0 at the LSB-position stage along the cascade toward the left to the outputs cn and sn-1 at the MSB-position stage [13], [39], [43], [57], [62].
In the introductory remarks of this section, it was suggested that addition could be performed within the execution time of a microinstruction. This time might typically be 50 to 100 ns in a 16-bit word-length computer. Now consider the delay of the n-bit ripple-carry adder of Fig. 2.3,b. Suppose that the delay from ci to ci+1 of any ADDER block is 10 ns. An n-bit addition can be performed in the time it takes the carry signal to reach the cn-1 position, followed by the delay in developing sn-1. Assuming this last delay is 15 ns, a 16-bit addition takes 15 × 10 + 15 = 165 ns.
There are two approaches that can be taken to reduce this 165-ns delay to the desired 50- to 100-ns range. The first approach, which is suggested by our earlier discussion, is to use faster electronic circuit technology in implementing the same ripple-carry design of Fig. 2.3,b. The second approach to reducing the n-bit adder delay is to use a logic network structure different from that shown in Fig. 2.3,b.
Logic structures for fast adder design must address the problem of speeding up the formation of the carry signals. Obviously, it is important to reduce the time required to form the ci inputs toward the MSB end of the adder. The usual two-level logic expression for si (sum) and ci+1 (carry-out) from Fig. 2.2 are
si =  and ci+1 = yici + xici + xiyi
and ci+1 = yici + xici + xiyi
Factoring the second of these into ci+1 = xiyi + (xi + yi)ci and defining a generative function Gi = xiyi and a propagate function Pi = xi + yi we can write ci+1 = Gi + Pi ci. Note that all the Gi and Pi functions for 0 ≤ i ≤ n - 1 can be formed independently and in parallel in one logic-gate delay after the X and Y vectors are available as parallel inputs to the n-bit adder. Expanding ci in terms of i - 1 subscripted variables and substituting into the ci+1 equation, we obtain
ci+1 = Gi + Pi Gi-1 + Pi Pi-1ci-1.
Continuing with this type of expansion, the final expression for any carry variable is
ci+1 = Gi + Pi Gi-1 + Pi Pi-1Gi-2 +?+ Pi Pi-1?P1G0 + Pi Pi-1?P0c0
Thus all carries can be obtained three logic-gate delays after the input operands X, Y, and c0 are available, because one delay is needed to develop all Pi and Gi signals, followed by two gate delays in the AND-OR circuit for ci+1. After another three gate-delays (one delay to invert the ci's and two delays to form si as shown earlier), all sum bits are available. Therefore, independent of n, the
n-bit addition process requires only six levels of logic.
A practical problem with this approach is that of gate fan-in constraints. The expression for ci+1 requires i + 2 inputs to the largest AND term and i + 2 inputs to the OR term. Due to electronic circuit considerations, logic gate fan-in is usually restricted to eight or less. Let us then consider the design of a 4-bit adder as a basic unit. The function
c4 = G3 + P3 G2 + P3P2G1 + P3P2P1G0 + P3P2P1P0c0
requires a fan-in of five for the basic gates, and needs two gate delays after the Gi and Pi functions are available. Using four of these connected as in Fig. 2.3c (with n = 4), a 16-bit adder is obtained that requires an amount of time equal to 12 gate delays. This total is composed of one delay for Gi and Pi formation, plus two each for c4, c8, c12, and c15 and a final three for s15. All other sum bits and c16 are available at or before the time for s15. In our earlier discussion that involved absolute time values, an implied gate delay of 5 ns was used because we let a two-level logic function (ci+1 for an ADDER function) have a delay of 10 ns. In those terms, this latest 16-bit adder requires 60 ns to develop all outputs as compared to the 165 ns required by the original Fig. 2.3b design. This is well within the previously stated 50- to 100-ns objective for the addition operation. Fast adders that form carry functions as in this example are called carry lookahead adders. Note that in the above 16-bit adder example, we have assumed that lookahead circuits form the carries inside of each block. However, they still ripple between blocks.
For longer word length and in higher-performance computers, it is necessary to speed up the addition operation even further. Applying the lookahead technique to the carry signals between blocks may do this. Thus a second level of lookahead is employed. We will illustrate this procedure by redesigning the above 16-bit adder. Suppose that each of the 4-bit adder blocks provides two new output functions defined as  and
and  , where k = 0 for the first 4-bit block, k = 1 for the second 4-bit block, etc. In the first block,
, where k = 0 for the first 4-bit block, k = 1 for the second 4-bit block, etc. In the first block,
 = P3P2P1P0 and
= P3P2P1P0 and  = G3 + P3G2 + P3P2G1 + P3P2P1G0
= G3 + P3G2 + P3P2G1 + P3P2P1G0
In words, if we say that Gi and Pi determine whether or not bit stage i generates or propagates a carry, then  and
and  determine whether or not block k generates or propagates a carry. With these new functions available, it is not necessary to wait for carries to ripple through blocks. For example, c16 can be formed as
determine whether or not block k generates or propagates a carry. With these new functions available, it is not necessary to wait for carries to ripple through blocks. For example, c16 can be formed as
c16 = 
using gates with a fan-in of five. The delay in developing c16 is two gate delays more than the time needed to develop the  and
and  functions. The latter require two and one gate delays, respectively, after the generation of Gi and Pi.Therefore c16 is available five gate delays after X, Y, and c0 are applied as inputs. Earlier, using only Gi and Pi functions, c16 required nine gate delays. Now consider that longer adders are constructed by cascading 16-bit basic blocks built using
functions. The latter require two and one gate delays, respectively, after the generation of Gi and Pi.Therefore c16 is available five gate delays after X, Y, and c0 are applied as inputs. Earlier, using only Gi and Pi functions, c16 required nine gate delays. Now consider that longer adders are constructed by cascading 16-bit basic blocks built using  and
and  functions as well as Gi and Pi functions. Then the total adder delay will be about half what it would have been if the longer adders had been built by cascading 4-bit basic blocks, using only Gi and Pi functions.
functions as well as Gi and Pi functions. Then the total adder delay will be about half what it would have been if the longer adders had been built by cascading 4-bit basic blocks, using only Gi and Pi functions.
Addition and Subtraction of Positive and Negative Numbers.Let us discuss why the 2?s-complement representation is a good choice. First, consider addition modulo N (mod N). A helpful graphical device for the description of addition mod N of positive integers is a circle with N values 0 through N ? 1 marked along its perimeter, as shown in Fig. 2.4,a. To treat some specific examples, we will choose N = 16. The operation (7 + 4) mod 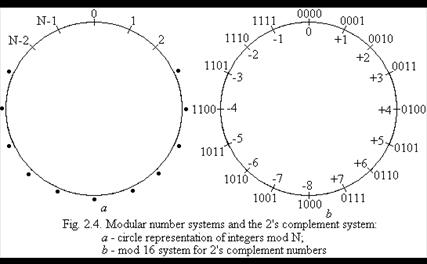 16 yields the value 11. To perform this operation graphically, locate 7 mod 16 = 7 on the circle and then step off 4 units in the clockwise direction to arrive at the answer 11. As a second example, consider (9 + 14) mod
16 yields the value 11. To perform this operation graphically, locate 7 mod 16 = 7 on the circle and then step off 4 units in the clockwise direction to arrive at the answer 11. As a second example, consider (9 + 14) mod
16 = 7, which is modeled on the circle by locating 9 mod 16 = 9 and stepping off 14 units in the clockwise direction to arrive at answer 7. This graphical technique works for the computation of (a + b) mod 16 for any positive numbers a and b; that is, locate a mod 16 and step off b units in the clockwise direction to arrive at (a + b) mod 16.
The n-bit positive-value adders of the previous two sections compute
S = (X + Y) mod 2n, where X and Y are in the range 0, 1, 2, ? , 2n?1. The overflow value cn, is 1 if X + Y ≥ 2n. Now consider a different interpretation of the mod 16 circle. Let the values 0 through 15 be represented by the 4-bit binary vectors 0000, 0001, ? , 1111, according to the binary number system, and then reinterpret these binary vectors to represent signed numbers in the range -8 through +7 in the 2?s-complement method, as shown in Fig. 2.4,b.
Let us apply the mod 16 addition technique discussed above to the simple example of adding +7 to -3. The 2's complement representation for these numbers is 0111 and 1101, respectively. To add these numbers, locate 0111 on the circle of Fig. 2.4b. Then step off 1101 (13) steps in the clockwise direction to arrive at 0100, which corresponds to +4. Alternatively, if we use one of the adder circuits for positive numbers, discussed earlier, we obtain
0 1 1 1
+ 1 1 0 1
Carry-out → 1 0 1 0 0
Note that if we ignore the carry-out from the fourth bit position in this addition, we obtain the correct answer. In fact, this is always the case.
We now state the rules governing addition and subtraction of n-bit signed numbers using the 2's-complement representation system.
1. To perform addition of two numbers, add their representations in an n-bit adder, ignoring the carry-out signal from the MSB position. The sum will be the algebraically correct value in the 2's-complement representations as long as the answer is in the range -2n-1 through +2n-1 -1.
2. To perform subtraction of two numbers X and Y, that is to perform X - Y, form the 2's complement of Y and then add it to X as in rule 1. Again, if the answer is in the range -2n-1 through +2n-1 - 1, the result will be the algebraically correct value in the 2's-complement representation system.
Fig. 2.5 shows some examples of addition and subtraction. In all these 4-bit examples the answers fall into the representable range of -8 through +7. When answers do not fall within the representable range, we say that an arithmetic overflow has occurred. The four addition operations (a) through (d) follow rule 1 above, and the six subtraction operations (e) through (j) follow rule 2. Note that the subtraction operation requires the subtrahend (bottom) value to be 2's complemented before the addition is performed. In the logic circuit implementation of subtraction, this complementation can be combined with the addition operation as shown in Fig. 2.6,a. The ADD/SUB control wire is set to 0 for addition. This allows the Y vector to be applied unchanged to one of the adder inputs along with a carry-in signal c0 of 0. When the ADD/SUB control wire is set to 1, signifying subtraction, the Y vector is 1's complemented (that is, bit complemented) by the XOR gates, and c0 is set to 1 to complete the 2's complementation of Y. Note that 2's complementing a negative value, as in Fig. 2.5,e, is done in exactly the same manner as 2's complementing a positive value.
| a | 0 0 1 0 + 0 0 1 1 0 1 0 1 | (+2) (+3) (+5) | b | 0 1 0 0 + 1 0 1 0 1 1 1 0 | (+4) (-6) (-2) |
| c | 1 0 1 1 + 1 1 1 0 1 0 0 1 | (-5) (-2) (-7) | d | 0 1 1 1 + 1 1 0 1 0 1 0 0 | (+7) (-3) (+4) |
| e | 1 1 0 1 - 1 0 0 1 | (-3) (-7) | => | 1 1 0 1 + 0 1 1 1 0 1 0 0 | ___ (+4) |
| f | 0 0 1 0 - 0 1 0 0 | (+2) (+4) | => | 0 0 1 0 + 1 1 0 0 1 1 1 0 | ___ (-2) |
| g | 0 1 1 0 - 0 0 1 1 | (+6) (+3) | => | 0 1 1 0 + 1 1 0 1 0 0 1 1 | ___ (+3) |
| h | 1 0 0 1 - 1 0 1 1 | (-7) (-5) | => | 1 0 0 1 + 0 1 0 1 1 1 1 0 | ___ (-2) |
| i | 1 0 0 1 - 0 0 0 1 | (-7) (+1) | => | 1 0 0 1 + 1 1 1 1 1 0 0 0 | ___ (-8) |
| j | 0 0 1 0 - 1 1 0 1 | (+2) (-3) | => | 0 0 1 0 + 0 0 1 1 0 1 0 0 | ___ (+5) |
| Fig. 2.5. 2's-complement ADD and SUBTRACT operations |
The logical simplicity and speed of performing either addition or subtraction of signed numbers in 2's-complement representation is the reason why this number representation is used in the ALU subsystems of most modern computers. It might seem that the 1's-complement representation would be just as good as the 2's-complement system for use in a combined addition-subtraction logic network. However, although complementation is easy, the result obtained after the add operation is not always correct. In fact, the carry-out cn cannot be ignored. If cn = 1, then 1 must be added to the result to make it correct; otherwise, if cn = 0, the result as obtained is correct. The requirement for this "correction cycle," which is conditional upon the carry-out from the add operation, means that addition and subtraction cannot be implemented as conveniently in the 1's complement system as in the 2's-complement system.
A 4-Bit ALU Circuit.The input and output variables for a typical 4-bit circuit are shown in Fig. 2.6,b. The three internal carries c1, c2, and c3, as well as the carry-out c4, are generated by lookahead logic. A number of these circuits can be cascaded as shown in Fig. 2.3,c to form adders of any desired length. If the carries c8, c12, etc., in such a cascade are not generated fast enough for some application, then the use of a second level of lookahead is facilitated by the provision of block propagate and generate variables PI and GI. External logic, using these variables, can directly generate the carries c8, c12, etc., faster than if they simply ripple between the blocks as in the cascade connection. The control inputs determine which function is performed on the input vectors X and Y to generate the output vector S. The versatility of these circuits as ALU building blocks is enhanced by inclusion of the operations AND, OR, XOR, etc., as well as addition and subtraction.

Overflow in Integer Arithmetic.When adding unsigned numbers, the carry-out cn serves as the overflow indicator. However, the case of signed numbers is slightly more involved. If we try to add the numbers +7 and +4 in the mod 16 adder of the previous section, the output vector S will be 1011, which is the code for -5, an obviously wrong result. The carry-out from the MSB position will be 0. Similarly, if we try to add -4 and -6, we get S = +6, another obvious error, and in this case the carry-out signal is 1. The addition of numbers with different signs clearly cannot cause overflow errors. The above discussion leads to the following conclusion:
1. The carry-out signal from the sign-bit position is not sufficient indicator of overflow in the case of signed-number addition.
2. The only possibility for overflow is when both operands have the same sign.
It is readily seen that an overflow has occurred whenever the sign of S does not agree with the sign of X and Y when the signs of X and Y are the same. In an n-bit adder, we can define an overflow signal Overflow by the logical expression
Overflow = 
For the case of combined addition-subtraction unit, such as that of Fig. 2.6a, the variable yn-1 in the Overflow expression should be taken from the output of the leftmost XOR gate. This will lead to the correct indication of overflow from either addition or subtraction.
Occurrence of an overflow is an important condition to detect in any computation. It is customary to dedicate a condition code flag as its indicator. It is possible to have this flag cause an interrupt when an add or subtract instruction results in an overflow. It is then the programmer's responsibility to decide on subsequent action.
Date: 2016-06-12; view: 367
| <== previous page | | | next page ==> |
| Element Base Development Influence on Data Processing | | | Operands Multiplication Operation |