
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
CHAPTER 9. Contracts 131 1 page
13579 10 8642
For Fernanda

|
[T]he problem of a rational economic order is determined precisely by the fact that the knowledge of the circumstances of which we must make use never exists in concentrated or integrated form, but solely as the dispersed bits of incomplete and frequently contradictory knowledge which all the separate
individuals possess__
The problem is thus in no way solved if we can show that all of the facts, if they were known to a single mind (as we hypothetically assume them to be
given to the observing economist) would uniquely determine the solution; instead, we must show how a solution is produced by the interactions of people, each of whom possesses only partial knowledge.
—Friedrich von Hayek.
"The Use of Knowledge in Society"

|
CONTENTS
Preface
Acknowledgments xv
chapter 1. Overview 3
chapter 2. Learning 25
2.1 Varieties of Learning Behavior 27
2.2 Recurrent Games 30
2.3 Fictitious Play 30
2.4 Potential Games 36
2.5 Nonconvergence of Fictitious Play 38
2.6 Adaptive Play 41
'CHAPTER 3. Dynamic and Stochastic Stability 44
3.1 Asymptotic Stability 44
3.2 Stochastic Stability 46
3.3 Elements of Markov Chain Theory 48
3.4 Perturbed Markov Processes 54
3.5 The Neighborhood Segregation Model 62
CHAPTER 4. Adaptive Learning in Small Games 66
4.1 Risk Dominance 66
4.2 Stochastic Stability and Risk Dominance in 2x2 Games 68
4.3 Who Goes First? 71
4.4 Playing the Field 72
4.5 Computing the Stationary Distribution 73
Chapter 5. Variations on the Learning Process 77
5.1 Heterogeneity in Information 71
5.2 Heterogeneity in Payoffs 80
5.3 Alternative Models of Noise 80
5.4 Unbounded Memory 83
5.5 Other Learning Models 89
contents
Chapter 6. Local Interaction 91
6.1 Games Played on Graphs 92
6.2 Interaction Structure and Speed of Adjustment 98
CHAPTER 7. Equilibrium and Disequilibrium Selection in
General Games 103
7.1Coordination Games 103
7.2Weakly Acyclic Games 106
7.3Curb Sets 109
7.4Elimination of Strictly Dominated Strategies 112
CHAPTER 8. Bargaining 113
8.1 Focal Points 113
8.2 Adaptive Learning in Bargaining 118
8.3 Sketch of the Proof of Theorem 8.1 120
8.4 Variations on the Bargaining Model 124
8.5 Heterogeneous Populations 126
8.6 Bargaining with Incomplete Information 128
8.7 Fifty-Fifty Division 129
CHAPTER 9. Contracts 131
9.1 Choice of Contracts as a Coordination Game 132
9.2 Maximin Contracts 133
9.3 A Contract Selection Theorem 134
9.4 The Marriage Game 136
9.5 Examples Showing Departures from Strict Efficiency and
Exact Maximin 138
9.6 Small Games and Symmetric Coordination Games 140
9.7 The Kalai-Smorodinsky Solution 141
9.8 Correlated Shocks 142
Chapter 10. Conclusion 144
Appendix: Proofs of Selected Theorems 151
Notes 173
Bibliography 177
| X |
Index 185
PREFACE
THIS BOOK is a slightly lengthened version of a series of lectures I gave in June 1995 at the Summer School in Economic Theory at the Institute for Advanced Studies of Hebrew University. The goal of the book is twofold. One is to suggest a reorientation of game theory in which players are not hyper-rational and knowledge is incomplete. In particular, I dispense with the notion that people fully understand the structure of the games they play, that they have a coherent model of others' behavior, that they can make rational calculations of infinite complexity, and that all of this is common knowledge. Instead, I postulate a world in wnich people base their decisions on limited data, use simple predictive models, and sometimes do unexplained or even foolish things. Over time, such simple adaptive learning processes can converge to quite complex equilibrium patterns of behavior. Indeed a surprising number rof classical solution concepts in game theory can be recovered via this route.
The second goal of the book is to suggest how this framework can be applied to the study of social and economic institutions. Here, I use "institution" in its everyday sense: "an established law, custom, usage, practice, organization" (Shorter Oxford English Dictionary). I take the view that institutions emerge over time from the cumulative experience of many individuals. Once their interactions coalesce into a settled pattern of expectations and behaviors, an "institution" has come into being. The theory makes qualitative predictions about the evolutionary paths that such processes tend tofollowand the diversity of institutional forms that they produce. The theory also tells us something about the welfare properties of these institutions. I illustrate these ideas through a variety of simple examples, including segregated neighborhood patterns, forms of economic contracts, terms of distributive bargaining, norms of cooperation, conventions of social deference, rules of the road, and so forth. These examples are illustrative and meant to suggest directions for future work; I do not pretend to give a definitive account of the history of any one institutional form.
Like all "new" approaches, the one presented here rests on ideas that have been around for a long time. Of particular importance is the work of Thomas Schelling, who to my knowledge was the first economist to show explicitly how micro decisions by many individuals evolve into recognizable patterns of macro behavior. If this book adds anything to his, it is to provide the analytical foundations for studying these kinds of models, and to widen their sphere of application. The second shoulder on which this book rests is the work of biologists Maynard Smith and Price. Like Schelling, they showed how game theory provides the crucial link between the micro behavior of individuals and the aggregate behavior of populations. As biologists, however, they were not motivated by the idea that individuals respond rationally to their environment. Instead, they maintained, poorly adapted individuals (animal or human) are weeded out by natural selection: those who play the game well breed faster than those who do not play as well. This yields an evolutionary selection process known as the replicator dynamic.
To study this selection dynamic, Maynard Smith and Price (1973) introduced a new equilibrium concept known as an evolntionarily stable strategy (ESS). An ESS is a frequency distribution of strategies in the population that cannot successfully be invaded by a small group of mutants. Any such distribution must be a Nash equilibrium of the underlying game, but not every Nash equilibrium is an ESS. The evolutionary perspective thus provides a novel twist to a classical solution concept in game theory, and suggests how it can be strengthened. For a more complete account of this approach, the reader is referred to the pioneering work of Maynard Smith (1982) and the superb surveys by Hofbauerand Sigmund (1988) and Weibull (1995).
This book takes a different approach, one that is closer in spirit to Schelling than to the biologists. First, my interest is in economic and social phenomena, not the behavior of mice and ants. This calls for a different class of adaptive dynamics. Second, the standard solution concept in this literature, ESS, is not sharp enough for my purposes. Indeed, it was dissatisfaction with this idea that led Dean Foster and me to formulate an alternative solution concept known as stochastic stability, which is the foundation of much that follows. Roughly speaking, an equilibrium is "stochastically stable" if it is robust against persistent random shocks, not just isolated shocks, as is assumed for ESS. This leads to a much sharper notion of equilibrium (and disequilibrium) selection, as 1 shall show in subsequent chapters.
The book is necessarily somewhat technical, but I have tried to keep it unencumbered by lengthy proofs, which have been relegated to the Appendix. A rudimentary acquaintance with game theory is presupposed; the required elements of dynamical systems theory and Markov processes are developed from scratch. The material should be easily accessible to graduate students and professional economists, and it is not beyond the reach of advanced undergraduates. The lectures were delivered in five sessions of about an hour and a half each. The book is longer, bu t not by much, so it can easily serve as a module in a traditional game theory course.

|

|
ACKNOWLEDGMENTS
THIS BOOK builds on the ideas of many others. I am particularly indebted to Dean Foster, who was a crucial partner in developing the general approach described here, and to Yuri Kaniovski, who introduced me to stochastic approximation theory and its application to urn schemes. Others whose work I draw on directly or indirectly include Brian Arthur, Robert Axtell, Ken Binmore, Larry Blume, Glenn Ellison, Joshua Epstein, Drew Fudenberg, Michihiro Kandori, Alan Kirman, David Levine, George Mailath, Richard Nelson, Georg Noldeke, Douglass North, Rafael Rob, Larry Samuelson, Andrew Schotter, Reinhard Selten, Robert Sugden, Fernando Vega-Redondo, Jorgen Weibull, and Sydney Winter.
The exposition benefited from comments by students at the Jerusalem Summer School in Economic Theory, the Stockholm School of Economics, the University of Paris, Johns Hopkins University, and the University of Chicago. I particularly want to express my appreciation to Marco Bassetto, Joe Harrington, Josef Hofbauer, Cassey Kim, Sung Kim, Stephen Morris, Adriano Rampini, Philippe Riviere, John Rust, and Sarah Stafford, who read the manuscript with a critical eye and offered many constructive suggestions. Special thanks are due to Todd Allen, who ran the simulations reported here. Peter Dougherty's enthusiasm for the project helped bring it to fruition; Lyn Grossman did a superb job of copyediting the final product.
I am indebted to the John D. and Catherine T. MacArthur Foundation, the Pew Charitable Trusts, and The Brookings Institution for providing generous financial support. The ideas expressed herein do not necessarily reflect the views of any of these institutions.
Finally, I owe a substantial intellectual debt to Kenneth Arrow and
Thomas Schelling, who have provided personal encouragement and
professional inspiration over many years. Debts like this can never be
properly repaid; one can only hope to pass them on to another generation.
Individual Strategy and Social Structure
A*

|
Chapter 1
OVERVIEW
economic and social institutions coordinate people's behaviors in various spheres of interaction. Markets coordinate the exchange of particular kinds of goods at specific times and places. Money coordinates trade. Language facilitates communication. Norms of etiquette coordinate how we interact socially with one another. The common law defines the bounds of acceptable behavior with respect to persons and property, and tells us what to expect when we overstep these bounds. These and many other institutions are the product, at least in part, of evolutionary forces. They are shaped by the cumulative impact of many individuals interacting with one another over long periods of time. Markets often grow up at convenient meeting places, such as a crossroads or a shady place (under the buttonwood tree). Customers come to expect particular kinds of goods to be offered there, and sellers come to meet their expectations. They also come to expect certain days and hours of operation, and particular procedures governing trade, whether posted price, haggling, or auction. These features are determined to a considerable degree by the accumulation of historical precedents, that is, by the decisions of many individuals who were concerned only with making the best trade at the moment, not with the impact of their decisions on the long-run development of that market.
A similar argument applies to economic contracts. When people rent apartments, for example, they are typically presented with a standard lease; usually the only things negotiated are price and the period of occupancy. People prefer standard contracts because they are more clearly enforceable in court than contracts that are fashioned on the spot. The accumulation of precedent makes them better defined, and hence more desirable to both parties to the transaction. But how do standard contracts become standard? The answer, evidently, is through a long period of experimentation with different forms. Eventually one form becomes standard and customary for a given type of transaction (in a given locale), not necessarily because it is optimal, but because it serves the purpose reasonably well and it is what everyone has come to expect. It is now an institution that coordinates behaviors, and to deviate from it would be costly.
A similar argument can be made for a great variety of social and economic institutions—language, codes of dress, forms of money and credit, patterns of courtship and marriage, accounting standards, rules of the road. In most cases, no one willed them into being: they are what they are due to the accumulation of precedent; they emerged from experimentation and historical accident.
Of course not all institutions can be explained in this way. Some were created by edict. In the Middle Ages, market towns were often established by royal charter. Rules of the road are enshrined in statutes. Accounting standards are regulated by official or semiofficial bodies. Languages are taught from standard dictionaries and grammar books. When we look more deeply into the matter, however, we find that these codifications were often just a way of ratifying practices that had already come into being through evolution. Furthermore, codifications and edicts do not stop evolution in its tracks: market towns come and go, accounting standards change, dictionaries and law books are always being rewritten.
The notion that economic institutions and patterns of behavior can be explained as the product or outcome of many individual decisions is scarcely a new idea in economics. It is perhaps most prominently associated with members of the Austrian school, notably Menger, von Hayek, and Schumpeter, though elements of the approach are implicit in the writings of earlier authors, including Adam Smith, David Hume, and Edmund Burke.1
What are the features that distinguish the "evolutionary" from the classical point of view in economics? One is the status accorded to equilibrium; the other is the status accorded to rationality. In neoclassical economics, equilibrium is the reigning paradigm. Individual strategies are assumed to be optimal given expectations, and expectations are assumed to be justified given the evidence. We, too, are interested in equilibrium, but we insist that equilibrium can be understood only within a dynamic framework that explains how it comes about (if in fact it does). Neoclassical economics describes the way the world looks once the dust has settled; we are interested in how the dust goes about settling. This is not an idle issue, since the business of settling may have considerable bearing on how things look afterwards. More important, we need to recognize that the dust never really does settle—it keeps moving about, buffeted by random currents of air. This persistent buffeting by random forces turns out to be an essential ingredient in describing how things look on average over long periods of time.
The second feature that differentiates our approach from standard ones is the degree of rationality attributed to economic agents. In neoclassical economic theory—especially game theory—agents are assumed to be hyper-rational. They know the utility functions of other agents (or the probability that other agents have these utility functions), they are fully aware of the process they are embedded in, they make optimum long-run plans based on the assumption that everyone else is making optimum long-run plans, and so forth. This is a rather extravagant and implausible model of human behavior, especially in the complex, dynamic environments that economic agents typically face. Moreover it represents a peculiar aberration from traditional ways of thinking in economics. One of the central messages of the pure theory of exchange, for example, is the ability of prices and markets to coordinate economic activity without assuming that agents are anything more than naive optimizers acting on limited information.
In this sense, our point of view represents a return to older traditions in economics. Agents adapt—they are not devoid of rationality—but they are not hyper-rational. They look around them, they gather information, and they act fairly sensibly on the basis of their information most of the time. In short, they are recognizably human. Even in such "low-rationality" environments, one can say a good deal about the institutions (equilibria) that emerge over time. In fact, these institutions are often precisely those that are predicted by high-rationality theories—the Nash bargaining solution, subgame perfect equilibrium, Pareto-efficient coordination equilibria, the iterated elimination of strictly dominated strategies, and so forth. In brief, evolutionary forces often substitute for high (and implausible) degrees of individual rationality when the adaptive process has enough time to unfold.
Let us add a little more meat to this rather skeletal outline. Recall that our general objective is to show how economic and social institutions emerge from the interactive decisions of many individuals. To talk about this idea rigorously, we need a model of how individuals interact at the micro level. This is naturally provided by a game, which describes the strategies available to each player and the payoffs that result when they play their strategies. Obviously the form of the game depends on the interactive situation we are trying to model. To illustrate ideas, we shall usually rely on games having a relatively sim- ple structure, such as coordination games and bargaining games, but the theory extends to all finite-strategy games, as we show in Chapter 7.
The framework differs from traditional game theory in several crucial respects, however. First, players are not fixed, but are drawn from a large population of potential players. Second, the probability that individuals interact depends on exogenous factors, such as where they live, and more generally on their proximity in some suitably defined social space. Third, agents are not perfectly rational and fully informed about the world in which they live. They base their decisions on fragmentary information, they have incomplete models of the process they are engaged in, and they may not be especially forward looking. Still, they are not completely irrational: they adjust their behavior based on what they think other agents are going to do, and these expectations are generated endogenously by information about what other agents have done in the past. On the basis of these expectations, the agent takes an action, which in turn becomes a precedent that influences the behavior of future agents. This creates a feedback loop of the following type:
Precedents —► Expectations
\ / Actions
Finally, we assume that the dynamic process is buffeted by random perturbations that arise from a variety of factors, such as exogenous shocks or unpredictability in people's behavior. These shocks play a role similar to that of mutations in biology by constantly testing the viability of the current regime. Moreover, they imply that the evolutionary dynamic never settles down completely; it is always in flux. The novel element of the approach from a technical standpoint is to show explicitly how to analyze the long-run behavior of such processes.
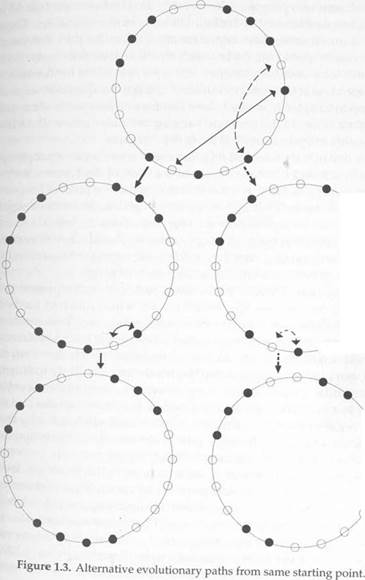
To illustrate these ideas concretely, consider the following variant of Schelling's model of neighborhood segregation patterns (Schelling, 1971, 1978). There are two types of people—As and Bs—who choose where they want to live. Their utility for a given location depends on the composition of the neighborhood, that is, on the mixture of As and Bs around them. The situation is depicted in Figure 1.1, where each circle represents a location. Let us suppose that an individual is discontent if his two immediate neighbors are unlike himself; otherwise, he is content. An equilibrium configuration is one in which no two individuals want to trade places. In other words, there is no pair such
 Figure 1.1. A random distribution of two types of agents on the circle.
Figure 1.1. A random distribution of two types of agents on the circle.
|
that one (or both) is currently discontent and both would be content after they trade locations. (If only one person is discontent beforehand, .. we can imagine that she compensates the other to move, so that both are better off after the move than they were before.)
We claim that if there are at least two people of each type, then in equilibrium no one is discontent. To see this, suppose to the contrary that an A is surrounded by two Bs (... BAB ...). Moving clockwise around the circle, let B* be the last B-type in the string of Bs who follow this A, and let A* be the person who follows B*:
... BAB... BB*A*______
Since there are at least two agents of each type, we can be sure that A' differs from the original A. But then the original discontented A could switch with B* (who is content), and both would be content afterwards. Thus we see that the equilibrium configurations consist of those arrangements in which everyone lives next to at least one person of their own type. No one is "isolated."
In general there are many types of equilibrium configurations. Some consist of small enclaves of As and Bs scattered around the landscape; others are completely segregated in the sense that all As live on one side of the circle, and all Bs on the other side (see Figure 1.2).
So much for the equilibrium analysis. What happens when the process begins in an out-of-equilibrium situation—will equilibrium even-
 Figure 1.2. Two equilibrium configurations: one segregated, the other integrated.
Figure 1.2. Two equilibrium configurations: one segregated, the other integrated.
|
tually be reached? Consider the following adjustment dynamic. Time is broken into discrete periods. In each period, two people meet at random and have a conversation about their respective neighborhoods. If they find that they can trade places to advantage, they do so. The reader may check that from any initial state, there always exists some sequence of advantageous trades that leads to an equilibrium. Since the number of states is finite and the probability of following such a path is positive, the process will eventually find its way to some equilibrium with probability one. Figure 1.3 illustrates a series of adjustments of this type. Note that the adjustment process is not fully predictable: where it ends up depends on where it starts and on the order in which people happened to trade. One can therefore speak of the probability of reaching various outcomes from some initial state, without knowing which one will in fact materialize. Such processes are sometimes said to be "path-dependent."2 Of course, any nontrivial stochastic process is path dependent in the sense that different paths will be followed depending on the outcome of chance events. A more telling definition of path dependency is that, with positive probability, the process follows paths that have different long-run characteristics (the process is "noner- godic"). The location model described above is path dependent in this sense, because the paths end up in different equilibrium configurations.
A further complication arises from the fact that people do not always act the way our models say they do. Suppose, for example, that there is a small probability that a pair of individuals who could gain from f
|
trading places will nevertheless fail to do so; similarly, there is a small probability that a pair who cannot gain from trading places will trade anyway. This assumption expresses the simple fact that we do not know all the reasons why people act the way they do. Our behavioral model is incomplete, and actions need to be modeled as random variables. These kinds of uncertainties have important implications for the behavior of the process. In particular, the process is ergodic, that is, its long-run average behavior is essentially independent of the path taken; furthermore it is independent of the initial conditions.3 Using techniques that we shall develop in Chapter 3, we shall show that the process spends almost all of its time in one of the completely segregated states where all As live on one side of the circle and all Bs on the other side.
Note that nobody intended this outcome; it arises because people optimize locally and do not worry about the effect of their actions on the long-run properties of the system. Note also that the process keeps on evolving—it never "ends up" somewhere—because the residential pattern of As and Bs is constantly shifting: sometimes As will live in the north, sometimes in the south; segregated neighborhoods will eventually become integrated, later they will become segregated again, and so forth. This represents a fairly accurate picture of reality.
While we cannot predict the dynamic path that such a process will follow, we can estimate the probability with which different kinds of residential patterns will be observed over the long run. In the present example, the answer is all too familiar: when people have a preference for some neighbors who are similar, and everyone is left to their own devices, completely segregated neighborhoods are more likely to emerge than any other pattern. In fact, this remains true even if everyone prefers to live in a mixed neighborhood (where one neighbor is similar and the other is different), than to live in a neighborhood surrounded by their own kind. In this case the segregated states may be far from optimal, but in the long run they are the most likely states.
The analytical techniques that allow us to prove this result are developed in subsequent chapters. There is, however, an important concept at work here that can be stated without the formal apparatus: when an evolutionary process is subjected to small, persistent stochastic shocks, some states occur much more frequently than others over the long run. These states are said to be stochastically stable (Foster and Young, 1990). Later we shall show how to compute the stochastically stable states explicitly. What bears emphasizing here is that stochastic stability is a considerably sharper (and more general) criterion of equilibrium selection than such established notions in the literature as "evolutionary stable strategy" and "risk-dominant equilibrium," though it is related to them in special cases, as we shall see in subsequent chapters.
To illustrate the kinds of questions we can address using this concept, let us briefly consider several further stylized examples. One economic institution that clearly has an evolutionary flavor is the choice of medium of exchange.4 History reveals the great variety of goods that societies have adopted as money: some used gold or silver; some, copper or bronze; others used beads; still others favored cattle. In the early stages of economic development, we can conceive of the choice of currency as growing out of individual decisions that gradually converge on some norm. Once enough people in a society have adopted a particular currency, everyone else wants to adopt it, too.
Date: 2016-04-22; view: 913
| <== previous page | | | next page ==> |
| The English Language | | | CHAPTER 9. Contracts 131 2 page |