General Plane Change Maneuver

In general, plane change maneuver involves the inclination and RAAN change while the size and shape of orbit remain the same. The change of the RAAN in plane change maneuver results that both orbit do not intersect at the original RAAN location. Figure 9-14 shows the example of general plane change maneuver.

Nodes 1 and 2 are the direction of RAAN for both initial and final orbits respectively, where else the is the eccentricity vector (also known as argument of perigee) for the initial orbit.

Figure 9-14.General Plane Change Maneuver. Figure 9-15.Argument of latitude of intersection point.

The delta-v required for the general plane change maneuver is shown in equation 9-17. The α angle is determined using equation 9-14, and A_La is the argument of latitude of intersection point, that is shown in Figure 9-15.

	(9‑14)
	(9‑15)
	(9‑16)
	(9‑17)

Example 9-9

Compute ΔV required to change the right ascension of the ascending node of the following orbit to 100o West: rp1 = 1.1DU, e1 = 0.1, i = 45˚ , Ω = 40˚ West, ω = 10˚

Solution

The orbit of satellite is transfer to Ω = 100˚ West. The ΔV required is given by, 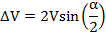where α is,   The speed of satellite at that particular point is, where, a = 1.22DU And r can be obtain through, ALa = 67.8˚ θ = ALa – ω = 57.8˚ Thus, V = 0.96 DU/TU ΔV = 0.679 DU/TU

Combined Maneuver

Frequently, the spacecraft orbit needs to be raised as well as titled. Two orbital transfers may then be applied:

-A coplanar maneuver to raise the orbit (change radius), then

-A plane change to tilt the orbit.

However, performing two separates orbit maneuvers is fuel inefficient because number of burns increased. Also, the time required for spacecraft to arrive at final orbit is much longer. Therefore, as an alternative, these two maneuvers can be combined in one maneuver to perform both tasks in one burn which is more economic (require less fuel) and faster.

There are a few type of combined maneuver available in study. In this section, we will introduce the minimum inclination maneuver.

Figure 9-16 shows the minimum inclination maneuver for a spacecraft. Both initial and final velocity of plane change maneuver contains the Hohmann transfer’s contribution. The change of inclination between initial, transfer and final orbit is chosen in the way such that the required cost is minimum. Here, a scaling term, s is introduced to determine change of inclination required between orbits.

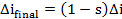
(9‑18)

Figure 9-16.Orbit transfer of a spacecraft using combined maneuver.

The total delta-v that required for the combined maneuver is,

+

(9-19)

Now, the optimum scaling, s is required to determine to produce minimum cost. Then, we take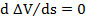

(9-18)

For circular initial and final orbits:

(9-19)

Example 9-10

Calculate the total delta-v required for a spacecraft to transfer from an orbit, r1 = 1.02 DU to r2 = 2.33 DU with the change of inclination ∆i = 10°.

Solution

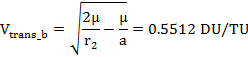
We have the initial and final radius, r1 and r2. Then semimajor axis for the transfer orbit is, The velocities at each location are: Then, we need to determine the scaling, s, that is:   Therefore, the total delta-v is,

Problems

1. A space vehicle in a circular orbit at an altitude of 0.0784 DU above the Earth executes a Hohmann transfer to a 0.1568 DU circular orbit. Calculate the total delta-v requirement.

2. Calculate the total delta-v required for a Hohmann transfer from a circular orbit of radius to a circular orbit of radius .

3. Determine the total time of flight for Hohmann and bi-elliptic transfer with given orbit properties:

i. Initial orbit, h_initial = 200 km,

ii. Apogee altitude of transfer orbit for bi-elliptic transfer, h_apog = 35000 km,

iii. Final orbit, h_final = 30000 km.

4. Determine the total ∆V required for a bi-elliptic transfer with given orbit properties:

i. Initial orbit, r₁ = 1.013 DU,

ii. Apogee altitude of transfer orbit, r₂ = 3.021 DU,

iii. Final orbit, r₃ = 2.601 DU.

i. Determine the total ∆V required and time-of-flight for a bi-elliptic transfer to place a spacecraft from r₁ = 6578.145 km into GEO. Given that, the apogee radius of transfer orbit is, r₂ = 46378.145 km.

ii. Given that the target and interceptor spacecraft are orbiting around the Earth in equatorial orbit. Determine the semimajor axis of the phasing orbit. Both spacecrafts’ positions at that time are:

iii. Given that the target and interceptor spacecraft are in an equatorial orbit with semimajor axis of 15000 km and eccentricity 0.1. Determine the semimajor axis of the phasing orbit if the distances of target and interceptor spacecraft to the Earth center are 13,574.4216 km and 13,615.9737 km respectively at the time. (Assume that the true anomaly of both spacecraft are in first quadrant.)

iv. Determine the ∆V required for a satellite to change its orbit plane from equatorial orbit to an orbit with inclination 10° at altitude 400km.

v. Determine the total ∆V required for a satellite to change its orbit plane at inclination 5° to GEO.

vi. Compute ΔV required to change from following orbit to the right ascension of the ascending node at 35˚ and inclination at 15˚:

r_p1 = 1.08 DU, e₁ = 0.05, i = 20˚ , Ω = 20˚, ω = 5˚

vii. Compute ΔV required to change from following orbit to the right ascension of the ascending node at 30˚ and inclination at 25˚:

Altitude, h = 300 km, e₁ = 0, i = 10˚ , Ω = 25˚

viii. Calculate the total delta-v required for a spacecraft to transfer from an orbit with altitude, h₁ = 400 km to geosynchronous orbit with the change of inclination ∆i = 25°.

ix. Calculate the total delta-v required for a spacecraft to transfer from an orbit, r₁ = 1.157 DU to r₂ = 4.136 DU with the change of inclination ∆i = 20° using:

a. Hohmann transfer followed by simple plane change.

b. Combined Maneuver.

References

Chobotov, V. (2002). Orbital Mechanics. Reston, Virginia, American Institute of Aeronautics and Astronautics, Inc.

Date: 2016-04-22; view: 1032