B)& If the potential energy of a system has not explicit time dependence.

*****

Time-dependent Shredinger equation can be used:

C)& Always.

*****

Partial solutions of time-independent and time-dependent Shredinger equations are connected by the ratio:

A)&

*****

The superposition principle:

A)& If a system can be found in states and then it can be found in the state too, where , are complex constants.

*****

The normality condition for a wave function has the view:

A)&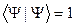

*****

The normality condition for a wave function has the view:

A)&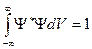

*****

Wave function of a free particle has a view:

E)&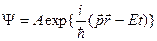

*****

De Broglie ratios between corpuscular properties of a particle and its wave properties are:

D)& ,

*****

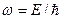
Eigen values of a hermitian operator cannot be by:

C)& complex numbers.

*****

Energy spectrum of a harmonic oscillator is

A)& equidistant.

*****

In Quantum Mechanics every physical quantity is associated with

D)& a linear hermitian operator.

*****

The kinetic energy operator in the coordinate representation has a view ( - Laplace operator):

D)&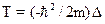

*****

It has no physical mean:

B)& a phase of a wave function.

*****

Eigen values of a hermitian operator are strictly:

B)& real numbers.

*****

Physical quantity F will take the same value after every measurement:

E)& If the state of a system is an eigen state for the operator F.

*****

Commutators of coordinate operators and momentum ones are equal to:

A)&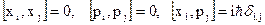

*****

Eigen functions of a hermitian operator:

A)& constitute a complete set of functions.

*****

An operator is

B)& Some action for transformation of one function in another one.

*****

Eigen values spectrum is degenerated if

A)& Some eigen functions correspond to one eigen value.

*****

Result of every measurement of some physical quantity is

A)& an eigen value of the corresponding operator.

*****

The quantum operators

Date: 2016-04-22; view: 945