Calibration Methods and Techniques

The methodology for making measurements is crucial to traceability and the decision making process. It calls for the integrated understanding and application of the following major elements:

1. The physical laws and concepts underlying the total measuring process

2. Reference standards

3. Instrumentation

4. Control and understanding of environmental effects (including operators or technicians) on the measurement process

5. Data reduction and analysis

6. Error estimation and analysis.

Calibration techniques vary depending on the category of equipment being calibrated. All measurements are the comparison of an unknown to a known and calibrations are no exception.

Say whether the following statements are true or false.

1. You need not put more resource into the calibration process to have ensured that things are working properly.

2. The minimum information that must be supplied is illustrated by the content of a typical NIST report.

3. Uncertainties are included in A NIST Report of Calibration.

4. The errors may never be greater than the reported uncertainty of the calibration.

5. Manufacturers and the calibration laboratories can help to minimize transport effects.

6. Artifact-based instruments and standards are absolutely stable with time.

7. All measurements are the comparison of a known to an unknown and calibrations are no exception.

Suggest the title to te text.

Make plan and retell the text according to it.

Unit 4

MEASUREMENT UNCERTAINTY

Practice reading the following words and word combinations.

Uncertainty, associated, specified, concise, significant, arguing, precision, perturbation, assessed, ascertain, non-eliminable, consequently, intrinsically, diverging, bias, robust, unfavourable, improvement, extending, compliance.

Uncertainty is a term used subtly in different ways in number of fields including philosophy, physics, statistics, economics, finance, engineering, information technologies. Comment on each point.

Look at the chart that shows the various categories of factors that contribute to measurement uncertainty. Discuss with a partner each category.

4. Read text A and answer the following questions:

1. What is measurement uncertainty?

2. Which way can measurement uncertainty be marked?

3. What does it depend on?

4. What’s the contribution of Gauss into measurement science? Was his theory complete?

5. What is the role of GUM?

6. What is the difference between random and systematic errors?

TEXT A

In metrology, measurement uncertainty describes a region about an observed value of a physical quantity which is likely to enclose the true value of that quantity. Assessing and reporting measurement uncertainty is fundamental in engineering, and experimental sciences such as physics.

It is a parameter, associated with the result of a measurement (eg a calibration or test) that defines the range of the values that could reasonably be attributed to the measured quantity. When uncertainty is evaluated and reported in a specified way it indicates the level of confidence that the value actually lies within the range defined by the uncertainty interval.

Measurement uncertainty may be denoted by error bars on a graph, or by the following notations:

· measured value ± uncertainty

· measured value(uncertainty)

The latter "concise notation" is used for example by International Union of Pure and Applied Chemistry (IUPAC) in stating the atomic mass of elements and by Committee on Data for Science and Technology (CODATA) in providing values for physical constants. There, the uncertainty applies only to the least significant figures of the measured value. For instance, 1.00794(7) stands for 1.007 94 ± 0.000 07, and 6.67428(67)×10⁻¹¹ stands for (6.674 28 ± 0.000 67) × 10⁻¹¹.

Measurement uncertainty is related with both the systematic and random error of a measurement, and depends on both the accuracy and precision of the measurement instrument. The lower the accuracy and precision of a measurement instrument are, the larger the measurement uncertainty is. Notice that both precision and measurement uncertainty are often determined as the standard deviation of the repeated measures of a given value. However, this is correct only when the instrument is accurate. When it is inaccurate, the uncertainty is larger than the standard deviation of the repeated measures.

At least since the late 1970s, the classical Gaussian error calculus has been considered incomplete. As is well established, Gauss exclusively considered random errors. Though Gauss also discussed a second type of error, which today is called unknown systematic error, he eventually dismissed suchlike perturbations, arguing that it would be up to experimenters to get rid of them.

To recall, by its very nature, an unknown systematic error is a time-invariant perturbation, unknown with respect to magnitude and sign. Any such measurement error can only be assessed by an interval the limits of which have to be ascertained on the part of the experimenter. As may be shown, it proves possible to keep the limits of such an interval symmetric to zero, e.g. .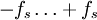

Unfortunately, contrary to Gauss's assumption, it turned out that unknown systematic errors proved to be non-eliminable. Consequently, the Gaussian error calculus had to be revised.

Measurement uncertainties have to be estimated by means of declared procedures. These procedures, however, are intrinsically tied to the error model referred to. Currently, error models and consequently the procedures to assess measurement uncertainties are considered highly controversial. As a matter of fact, today the metrological community is deeply divided over the question as to how to proceed. For the time being, all that can be done is to put the diverging positions side by side.

Within the scope of Legal Metrology and Calibration Services, measurement uncertainties are specified according to the ISO Guide to the Expression of Uncertainty in Measurement (abbreviated GUM). GUM's idea is to transfer time-constant unknown systematic errors formally into random errors. In fact, the GUM "randomizes" systematic errors by means of a postulated rectangular distribution density.

In contrast to the proceeding of the GUM, a diverging approach has been proposed. It reformulates the Gaussian error calculus on a different basis, namely by admitting biases expressing the influence of the time-constant unknown systematic errors. Biases call into question nearly all classical procedures of data evaluation such as Analysis of Variance, but in particular those in use to assess measurement uncertainties.

The alternative concept maps unknown systematic errors as stipulated by physics, namely as quantities constant in time. Unknown systematic errors are not treated by means of postulated probability densities.

Right from the outset, the flow of random and systematic errors get strictly separated. While the influence of random errors is brought to bear by a slight, but, in fact, rather useful modification of the classical Gaussian error calculus, the influence of systematic errors is carried forward by uniquely designed, path-independent, worst-case estimations.

Uncertainties of this type are reliable and robust and withstand computer simulations, even under unfavourable conditions.

With regard to the setting of weights in least squares adjustments, the alternative approach safeguards the localization of the true values of the measurands for any choice of weights.

Date: 2016-04-22; view: 969