Free Space Propagation

The benchmark by which we measure the loss in a transmission link is the loss that would be expected in free space - in other words, the loss that would occur in a region which is free of all objects that might absorb or reflect radio energy. This represents the ideal case which we hope to approach in our real world radio link (in fact, it is possible to have path loss which is less than the "free space" case, as we shall see later, but it is far more common to fall short of this goal).

Calculating free space transmission loss is quite simple. Consider a transmitter with power P_t coupled to an antenna which radiates equally in all directions (everyone's favorite mythical antenna, the isotropic antenna). At a distance d from the transmitter, the radiated power is distributed uniformly over an area of 4 d² (i.e. the surface area of a sphere of radius d), so that the power flux density is:

(1)

The transmission loss then depends on how much of this power is captured by the receiving antenna. If the capture area, or effective aperture of this antenna is A_r, then the power which can be delivered to the receiver (assuming no mismatch or feedline losses) is simply

(2)

For the hypothetical isotropic receiving antenna, we have

(3)

Combining equations (1) and (3) into (2), we have

(4)

The free space path loss between isotropic antennas is P_t / P_r. Since we usually are dealing with frequency rather than wavelength, we can make the substitution = c/f (where c, of course, is the speed of light) to get

(5)

This shows the classic square-law dependence of signal level versus distance. What troubles some people when they see this equation is that the path loss also increases as the square of the frequency. Does this mean that the transmission medium is inherently more lossy at higher frequencies? While it is true that absorption of RF by various materials (buildings, trees, water vapor, etc.) tends to increase with frequency, remember we are talking about "free space" here. The frequency dependence in this case is solely due to the decreasing effective aperture of the receiving antenna as the frequency increases. This is intuitively reasonable, since the physical size of a given antenna type is inversely proportional to frequency. If we double the frequency, the linear dimensions of the antenna decrease by a factor of one-half, and the capture area by a factor of one-quarter. The antenna therefore captures only one-quarter of the power flux density at the higher frequency versus the lower one, and delivers 6 dB less signal to the receiver. However, in most cases we can easily get this 6 dB back by increasing the effective aperture, and hence the gain, of the receiving antenna. For example, suppose we are using a parabolic dish antenna at the lower frequency. When we double the frequency, instead of allowing the dish to be scaled down in size so as to produce the same gain as before, we can maintain the same reflector size. This gives us the same effective aperture as before (assuming that the feed is properly redesigned for the new frequency, etc.), and 6 dB more gain (remembering that the gain is with respect to an isotropic or dipole reference antenna at the same frequency). Thus the free space path loss is now the same at both frequencies; moreover, if we maintained the same physical aperture at both ends of the link, we would actually have 6 dB less path loss at the higher frequency. You can picture this in terms of being able to focus the energy more tightly at the frequency with the shorter wavelength. It has the added benefit of providing greater discrimination against multipath - more about this later.

The free space path loss equation is more usefully expressed logarithmically:

(f in MHz, d in km) (6a)

or

(f in MHz, d in miles) (6b)

This shows more clearly the relationship between path loss and distance: path loss increases by 20 dB/decade or 6 dB/octave, so each time you double the distance, you lose another 6 dB of signal under free space conditions.

Of course, in looking at a real system, we must consider the actual antenna gains and cable losses in calculating the signal power P_r which is available at the receiver input:

(7)

where

P_t = transmitter power output (dBm or dBW, same units as P_r)

L_p = free space path loss between isotropic antennas (dB)

G_t = transmit antenna gain (dBi)

G_r = receive antenna gain (dBi)

L_t = transmission line loss between transmitter and transmit antenna (dB)

L_r = transmission line loss between receive antenna and receiver input (dB)

A table of transmission line losses for various bands and popular cable types can be found in the Appendix.

Example 1.Suppose you have a pair of 915 MHz WaveLAN cards, and want to use them on a 10 km link on which you believe free space path loss conditions will apply. The transmitter power is 0.25 W, or +24 dBm. You also have a pair of yagi antennas with 10 dBi gain, and at each end of the link, you need about 50 ft (15 m) of transmission line to the antenna. Let's say you're using LMR-400 coaxial cable, which will give you about 2 dB loss at 915 MHz for each run. Finally, the path loss from equation (6a) is calculated, and this gives 111.6 dB, which we'll round off to 112 dB. The expected signal power at the receiver is then, from (7):

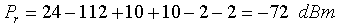
According to the WaveLAN specifications, the receivers require -78 dBm signal level in order to deliver a low bit error rate (BER). So, we should be in good shape, as we have 6 dB of margin over the minimum requirement. However, this will only be true if the path really is equivalent to the free space case, and this is a big if! We'll look at means of predicting whether the free space assumption holds in the next section.

Date: 2016-03-03; view: 746