Subjective Expected Utility Theory

The previous section discussed preferences among riskless options. However, selecting among risky options in which outcomes occur with some probability is even more difficult. For example, a firm may have to select between a set of new products to develop, each with probabilities of profits and losses. One of the simplest ways of placing a value on a risky proposition is by calculating its EV, which is the sum of each outcome multiplied by its associated probability (i.e., EV = XpjXi). A new product with a 75% chance of making $15 mil­lion in profits and a 25% chance of failing, with a loss of a million in development costs would have an EV = .75* ($15M) + .25*($- lM) = $11.75Minexpectedprofits.This is the amount of money the firm would make on average if they repeatedly marketed new products with these probabil­ity-outcome characteristics. Clearly, such a calculation would be an imperfect guide to decision making in any single case. It can be easily shown that our preferences for risky propositions are not always consistent with an EV model. For example, how much would you pay for a gamble in which you flip a coin until the first head appears (on the nth flip) ^

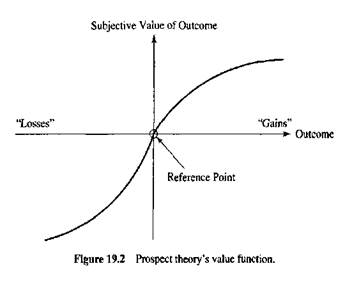
In a second modification of EUT, prospect theory pro­posed a value function that was a significant departure from the previous utility functions (Figure 19.2). Most earlier util­ity functions defined subjective value with respect to overall wealth. The prospect theory value function defines value with respect to a reference point (or the status quo). Second, the value function for the domain of losses (relative to the refer­ence point) is steeper than is that for gains. This leads to a result called loss aversion in which losses are more painful than equal magnitude gains are pleasurable. Finally, the value function is concave (risk averse) above the reference point and convex (risk seeking) below it. Because identical options can often be described in terms of different reference points, this raises the possibility that different ways of describing the same problem may shift choices from risk seeking to risk averse. This general framing problem is discussed in the fol­lowing section.

Framing

To illustrate framing, consider the following options de­scribed by Hogarth (1987). He presented MBA subjects with a riskless option and a risky option, as follows:

Imagine that you have just learned that the sole supplier of a crucial component is going to raise prices. The price in­crease is expected to cost the company $6 million. Two alterna­tive plans have been formulated to counter the effect of the price increase. The anticipated consequences of these plans are as follows:

One group was given Set I and asked to select between Plans AandB:

Plan A the company will save $2 million Plan B 1/3 probability that $6 million will be saved 2/3 probability that nothing will be saved

Another group of people were asked to select between Plan C and D in Set II:

Plan C the company will lose $4 million

Plan D 1/3 probability that there will be no loss

2/3 probability that the company will lose

$6 million

Notice that the information in the two formulations is identical and that Plan A = Plan C and Plan B = Plan D. How­ever, information is framed differently in the two choice sets' it is framed positively (i.e., money saved) in Plans A and B and negatively (i.e., money lost) in Plans C and D. Framing of the information is similar to the "glass half-empty/half-full" description of optimistic/pessimistic perspectives.

The majority of subjects select the riskless option (Plan A) over the risky option (Plan B) in Set I but select the risky op­tion over the riskless option (Plan D over C) in Set II, result­ing in a reversal of preferences. According to prospect theory, risk attitudes are not simply a characteristic of the individual decision maker but depend on the context in which options are evaluated. Because of the differing shapes of the value functions for the domains of gains and losses, people are risk averse when options are framed positively and risk seeking when options are framed negatively.

Another type of framing, attribute framing, has been shown for riskless options. For example, Levin and Gaeth (1988) showed that subjects evaluated ground beef more fa­vorably when it was described as 75% lean than as 25% fat (although this advantage drastically diminished after con­sumers tasted the beef). The credit card lobby insists on using the label "cash discount" rather than "credit card surcharge" for gas stations that charge higher prices when customers use their credit cards instead of cash (Thaler, 1980).

Date: 2016-03-03; view: 2373