Product Example of Parameter Design (Norrell)

Returning to the NerFM Missilestorm™ application, the design variables, noise variables, and performance metric have all been chosen. In addition, an experimental matrix has been configured. The experiment must now be conducted for each combination of design variables and noise variables. The trails in the experimental matrix, Table 19.4, are randomized to avoid experimental bias. Blocking of the effects is also considered; however, the experiments will not require a change in environmental conditions or multiple days.

Table 19.5 shows the results of the experiments, where the "run #" corresponds to the randomized order for the trails during testing. As a first step in analyzing the data, ANOVA is applied to the results, averaging across the noise variable. Table 19.6 lists the ANOVA results. Based on the ANOVA analysis, a modest confidence level gives the following phenomenological model:

Assuming that this model reflects maximum distance, we want to maximize y, and chose 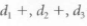- (curved fins with graphite and full cavity), which gives an output of 10.0 meters. These results are a bit counterintuitive in that a spinning missile's drag (due to a curved fin arrangement) would lead one to think it would decrease maximum distance (part of the energy is used in rotation instead of linear translation). However, interactions between the three design variables have a greater benefit than the loss seen due to spinning-missile drag.

How does this result compare with the stock missile maximum distance? From tests with the missiles as purchased, the mean stock maximum distance is 8.78 meters. At 10.0 meters, we have produced approximately a 15% improvement in maximum distance. But is this design robust? Let's consider an analysis of the results as an inner-outer array. Equation 19.9 may then be applied to calculate the signal-to-noise ratios across the design variables. Table 19.7 lists the results of this extended analysis.

As shown in the table, largest signal-to-noise ratio is seen with d₁ +, d₂ +, d₃ -. However, all of the S/N ratios are relatively high. When this case occurs, we have several options. The first option is to add other constraints to the problem and determine if these constraints aid us in choosing the final design variable values. For instance, one variable set may offer much cheaper manufacturing with only a slight loss in signal to noise ratio. Another option is to select the variable set which maximizes our model if it doesn't cause a drop in the S/N ratio. In this instance, d₁ +, d₂ +, d₃ - gives both the highest S/N ratio and maximizes the output of maximum distance. If we consider variance in the data, reflected by the error column in the ANOYA, we see that this factor combination also has one of the lower magnitudes of experimental errors. Thus, the variable set of d₁ +, d₂ +, d₃ -. - not only maximizes flight distance, but it also gives the highest signal-to-noise ratio and the smallest variance. It is chosen as the preferred design configuration for a robust product.

IV. CHAPTER SUMMARY AND "GOLDEN NUGGETS"

Date: 2016-03-03; view: 1039