Noise Variable Matrix

Consider a noise variable that behaves according to a normal distribution. To characterize this variable, two statistical parameters are needed: an average and a standard deviation. The question arises: how do we choose experimental values, assuming a normal distribution for the noise variables?

For two-level experimentation, one thought is to experiment at the points 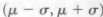On the other hand, why not 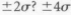? Or perhaps the 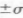is a good idea, to stay close to the average. To consider this decision, the philosophy of robustness must be applied.

A design team wants the product to be robust-to work in all circumstances. Given this desire, the next observation is that the product will be subject to the extreme tails of the noise distribution at some point in the product life cycle. These conditions are usually difficult to satisfy; however, if the product does work at these points, then it works very well at more typical operating points.

These observations and philosophy then answer the question of this section. For a product to be robust, then one should always experiment at the limits of the distribution. One should attack the limits-experiment at points 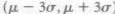, since if the products works at these points, it will work virtually always. It will be a robust product. If there are m noise variables, the limits define M=2^m possible values for experimentation. This approach assumes the measured response will behave linearly for the range defined by the limits. This approach is also excessive from a resource viewpoint. M experiments will be quite large, even for a small number of variables, m.

Thus, the number of experimental cases must be pared down to something that is physically possible, given finite resources. To carry out this pruning operation, we apply orthogonality conditions on the experiments, and use the experimental matrices of Appendix B. This amended approach reduces to a small reasonable number for M. The allocation results in a noise matrix, shown in Table 19.1, which is an allocation of noise variable values to noise experimental arrangements.

It should be noted that the experimental matrices provided in Appendix B must be used thoughtfully. A number of assumptions are made regarding the variables in the matrix. First, only a finite set of noise variables will impact the product performance. Second, the higher order effects of the noise variables are negligible, except where explicitly chosen for a given experimental matrix. Third, the product performance may be represented between the chosen noise variable limits, but not necessarily extrapolated outside these limits.

Date: 2016-03-03; view: 704