
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
II. Produit scalaire de deux vecteurs
CHAPITRE I
Eléments de la théorie des déterminants
I. Déterminants du deuxième ordre
1. Calculer les déterminants:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
2. Résoudre les équations:
1)  ; 2)
; 2) 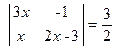 ; 3)
; 3)  ; 4)
; 4)  ;
;
5) 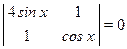 ; 6)
; 6)  .
.
3. Résoudre les inégalités:
1)  ; 2)
; 2) 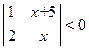 ; 3)
; 3) 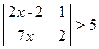 ; 4)
; 4)  .
.
II. Déterminants du troisième ordre
1. Calculer les déterminants:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 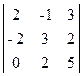 ; 5)
; 5) 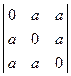 .
.
2. Résoudre les équations:
1)  ; 2)
; 2)  .
.
3. Résoudre les inégalités:
1)  ; 2)
; 2)  .
.
4. Calculer les déterminants en utilisant les propriétés:
1) 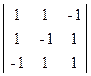 ; 2)
; 2) 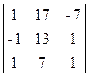 ; 3)
; 3) 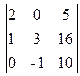 ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  .
.
5. On demande de démontrer les égalités sans développer les déterminants:
1)  ; 2)
; 2) 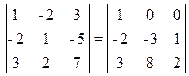 .
.
III. Résolution et étude d’un système de deux équations du premier degré à deux inconnues et d’un système de trois équations du premier degré à trois inconnues
Trouver toutes les solutions des systèmes d’équations ci-dessous:
1) {  2) {
2) { 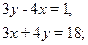 3) {
3) {  4) {
4) { 
5) {  6) {
6) { 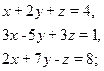 7) {
7) {  8) {
8) { 
IV. Systèmes de deux équations homogènes du premier degré à trois inconnues
Trouver toutes les solutions des systèmes d’équations ci-dessous:
1) {  2) {
2) {  3) {
3) { 
4) {  5) {
5) { 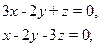 6) {
6) { 
V. Déterminants du quatrième ordre
Calculer les déterminants du quatrième ordre:
1)  ; 2)
; 2)  ; 3)
; 3) 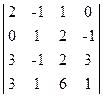 ; 4)
; 4)  .
.
Réponses
I. 1. 1) 18; 2) 10; 3) 0; 4) 0; 5) 1.
2. 1) (1; -4); 2) ( 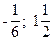 ); 3) (
); 3) (  ); 4) (
); 4) (  );
);
5) 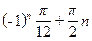 , où n est un nombre entier quelconque;
, où n est un nombre entier quelconque;
6)  , où n est un nombre entier quelconque.
, où n est un nombre entier quelconque.
3. 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
II. 1. 1) -12; 2) 29; 3) 87; 4) 0; 5) -29; 6)  .
.
2. 1) -3; 2) (-10; 2).
3. 1) (3,5; +¥); 2) (-6; -4).
4. 1) -4; 2) 180; 3) 87; 4) 0; 5)  ; 6)
; 6)  ;
;
7) 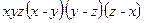 ; 8)
; 8)  .
.
III. 1. (16; 7);
2. (2; 3);
3. Le système admet une infinité de solutions différentes, chacune d’entre elles peut se calculer à l’aide de la formule  où les valeurs numériques de x sont choisies arbitrairement.
où les valeurs numériques de x sont choisies arbitrairement.
4. Le système n’a pas de solutions.
5. (24,5; 21,5; 10).
6. (1; 1; 1).
7. (2; 3; 4).
8. (1; 3; 5).
IV. 1. (-2t; 7t; 4t), où t est un réel arbitraire.
2. (2t; 3t; 0), où t est un réel arbitraire.
3. (0; t; 3t), où t est un réel arbitraire.
4. (0; t; 2t), où t est un réel arbitraire.
5. (2t; 5t; 4t), où t est un réel arbitraire.
6. (4t; 2t; 3t), où t est un réel arbitraire.
V. 1. 30; 2. -20; 3. 0; 4. 48.
CHAPITRE II
I. Algèbre vectorielle
1. Notion de vecteur. Projection d’un vecteur sur un axe
Formules
1. 
|
2. 
|
3.Si  sont les angles formés par le vecteur sont les angles formés par le vecteur  avec les axes de coordonnées, avec les axes de coordonnées,  s’appellent cosinus directeurs du vecteur s’appellent cosinus directeurs du vecteur 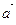 et ils sont égaux à: et ils sont égaux à:

|
Problèmes
1. Calculer le module du vecteur  .
.
2. On donne deux premières coordonnées d’un vecteur:  . Calculer sa troisième coordonnée z de manière que
. Calculer sa troisième coordonnée z de manière que  .
.
3. On donne les points A(3, -1, 2) et B(-1, 2, 1). Calculer les coordonnées des vecteurs  et
et  .
.
4. Calculer les coordonnées du point N qui coïncide avec l’extrémité du vecteur 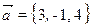 si le point M (1, 2, -3) coïncide avec son origine.
si le point M (1, 2, -3) coïncide avec son origine.
5. Calculer les coordonnées de l’origine du vecteur  si son extrémité coïncide avec le point (1, -1, 2).
si son extrémité coïncide avec le point (1, -1, 2).
6. On donne le module 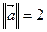 d’un vecteur et les angles
d’un vecteur et les angles 

 . Calculer les projections du vecteur donnée sur les axes de coordonnées.
. Calculer les projections du vecteur donnée sur les axes de coordonnées.
7. Calculer les cosinus directeurs du vecteurs  .
.
8. Calculer les cosinus directeurs du vecteurs  {
{ 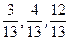 }.
}.
9. Est-ce qu’un vecteur peut former avec les axes de coordonnées les angles suivants:
1)  α = 45°, b = 60°, g = 120°;
α = 45°, b = 60°, g = 120°;
2) α = 45°, b = 135°, g = 60°;
3) α = 90°, b = 150°, g = 60° ?
10. Est-ce qu’un vecteur peut former avec deux axes de coordonnées les angles suivants:
1)  α = 30°, b = 45°;
α = 30°, b = 45°;
2)  α = 60°, b = 60°;
α = 60°, b = 60°;
3)  α = 150°, b = 30° ?
α = 150°, b = 30° ?
Réponses
1.  . 2.
. 2.  . 3.
. 3.  . 4. N (4, 1, 1). 5. (-1, 2, 3). 6.
. 4. N (4, 1, 1). 5. (-1, 2, 3). 6.  . 7.
. 7.  . 8.
. 8.  .
.
9. 1) Oui. 2) Non. 3) Non. 10. 1) Non. 2) Oui. 3) Non.
2. Opérations linéaires effectuées avec les vecteurs
Formules
1. 
|
2. 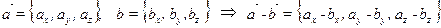 
|
3.  
|
4.Si 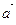 et et  sont collinéaires, alors sont collinéaires, alors 
|
5.Si 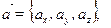 alors alors 
|
Problèmes
- Etant donnés deux vecteurs
 et
et  , construire les vecteurs suivants:
, construire les vecteurs suivants:  +
+  ;
;  -
-  ;
;  -
-  ; -
; -  -
-  .
. - Etant donnés deux vecteurs
 et
et  , construire les vecteurs suivants: 3
, construire les vecteurs suivants: 3  ,
,  ,
,
2  -
- 
 ,
, 

 - 3
- 3  .
.
- Construire le vecteur
 , si
, si
1) 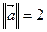 ,
, 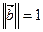 et (
et (  ^
^  ) =
) =  ;
;
2) 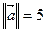 ,
, 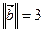 et (
et (  ^
^  ) =
) =  .
.
- Construire le vecteur
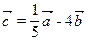 , si
, si
1)  ,
,  et (
et (  ^
^  ) =
) =  ;
;
2)  ,
,  et (
et (  ^
^  ) =
) =  .
.
- Construire le vecteur
 , si
, si  ,
,  et (
et (  ^
^  ) =
) =  .
. - Construire le vecteur
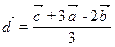 si
si  ,
,  ,
, 
- Construire le vecteur
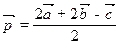 si
si  ,
,  ,
, 
- Construire le vecteur
 si
si  ,
, 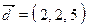 ,
, 
- A quelles conditions doivent satisfaire les vecteurs
 et
et  pour que l’on dise les relations suivantes:
pour que l’on dise les relations suivantes:
1)  ; 2)
; 2) 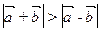 ; 3)
; 3) 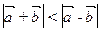 ?
?
- A quelles conditions doivent satisfaire les vecteurs
 et
et  pour que le vecteur
pour que le vecteur  +
+  divise l’angle formé par les deux premiers vecteurs en deux angles égaux ?
divise l’angle formé par les deux premiers vecteurs en deux angles égaux ? - Soient donnés les vecteurs:
 et
et  . Calculer les projections sur les axes de coordonnées des vecteurs suivants:
. Calculer les projections sur les axes de coordonnées des vecteurs suivants:
1)  +
+  ; 2)
; 2)  -
-  ; 3) 2
; 3) 2  ; 4)
; 4) 
 ; 5) 2
; 5) 2  + 3
+ 3  ; 6)
; 6) 
 -
-  .
.
- Vérifier que les vecteurs
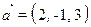 et
et  sont collinéaires. Etablir celui qui est plus long que l’autre et de combien de fois et s’ils sont de même sens ou de sens opposé.
sont collinéaires. Etablir celui qui est plus long que l’autre et de combien de fois et s’ils sont de même sens ou de sens opposé. - Calculer pour quelles valeurs de α et b les vecteurs
 et
et  sont collinéaire?
sont collinéaire? - Vérifier que les quatre points A (3, -1, 2), B (1, 2, -1), C (-1, 1, -3) et D (3, -5, 3) sont les sommets d’un trapèze.
- On donne les points A (-1, 5, -10), B (5, -7, 8), C (2, 2, -7) et D (5, -4, 2). Vérifier que les vecteurs
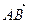 et
et  dire celui qui est le plus long, de combien de fois et s’ils sont de même sens ou de sens opposé.
dire celui qui est le plus long, de combien de fois et s’ils sont de même sens ou de sens opposé. - Trouver le vecteur unitaire du vecteur
 .
. - Trouver le vecteur unitaire du vecteur
 .
. - Calculer les modules de la somme et de la différence des vecteurs
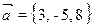 et
et  .
. - Calculer les modules de la somme et de la différence des vecteurs
 et
et  .
.
Réponses
9. 1) Les vecteurs  et
et  doivent être perpendiculaires.
doivent être perpendiculaires.
2) L’angle formé par les vecteurs  et
et  doit être aigu.
doit être aigu.
3) L’angle formé par les vecteurs  et
et  doit être obtus.
doit être obtus.
10. 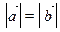 .
.
11. 1) { 1, -1, 6 }; 2) { 5, -3, 6 }; 3) { 6, -4, 12 }; 4) { 1, -  , 0 }; 5) { 0, -1, 12 }; 6) { 3, -
, 0 }; 5) { 0, -1, 12 }; 6) { 3, - 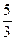 , 2 }.
, 2 }.
12. Le vecteur  est trois fois plus long que le vecteur
est trois fois plus long que le vecteur  ; ils sont orientés en sens contraires.
; ils sont orientés en sens contraires.
13. 4; -1.
14. Le vecteur  est deux fois plus que le vecteur
est deux fois plus que le vecteur  ; ils sont de même sens.
; ils sont de même sens.
16.  {
{  }. 17. {
}. 17. {  }. 18. 6; 14. 19.
}. 18. 6; 14. 19. 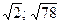 .
.
II. Produit scalaire de deux vecteurs
Formules
1. 
|
2. 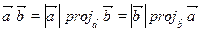
|
3. 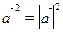
|
4. 
|
5. 
|
6.   ; ; 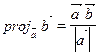
|
7.  est une conditionnécessaire et suffisante pour que deux vecteurs soient perpendiculaires. est une conditionnécessaire et suffisante pour que deux vecteurs soient perpendiculaires.
|
Problèmes
- Les vecteurs
 et
et  forment un angle
forment un angle  . Si l’on sait que
. Si l’on sait que  ,
,  , calculer
, calculer
1)  ; 2)
; 2) 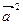 ; 3)
; 3)  ; 4)
; 4)  ; 5) (3
; 5) (3  - 2
- 2  )(
)(  +2
+2  ); 6) (
); 6) (  -
-  )2; 7) (3
)2; 7) (3  +2
+2  )2.
)2.
- Les vecteurs
 et
et  sont perpendiculaires. Le vecteur
sont perpendiculaires. Le vecteur  forme avec eux les angles égaux à
forme avec eux les angles égaux à  . Si l’on sait que
. Si l’on sait que 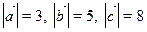 , calculer:
, calculer:
1) (3  - 2
- 2  )(
)(  +3
+3  ); 2) (
); 2) (  +
+  +
+  )2; 3) (
)2; 3) (  +2
+2  - 3
- 3  )2.
)2.
- On donne
 . Déterminer la valeur de
. Déterminer la valeur de  pour laquelle les vecteurs
pour laquelle les vecteurs  et
et  sont perpendiculaires.
sont perpendiculaires. - On donne les vecteurs
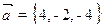 et
et  . Calculer:
. Calculer:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) (2
; 4) (2  - 3
- 3  )(
)(  +2
+2  ); 5) (
); 5) (  +
+  )2;
)2;
6) (  -
-  )2.
)2.
- Calculer le travail accompli par la force
 lorsque son point d’application se déplace de l’origine à l’extrémité du vecteur
lorsque son point d’application se déplace de l’origine à l’extrémité du vecteur  .
. - On donne les points
 . Calculer:
. Calculer:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ;
;
5)  .
.
- Calculer le travail accompli par la force
 lorsque son point d’application en se déplaçant suivant une trajectoire rectiligne, en passant du point
lorsque son point d’application en se déplaçant suivant une trajectoire rectiligne, en passant du point  au point
au point  .
. - On donne trois forces:
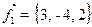 ,
,  et
et  appliquées en un même point. Calculer le travail effectué par la résultante de ces trois forces si le point concidéré se déplace suivant une trajectoire rectiligne, en passant du point
appliquées en un même point. Calculer le travail effectué par la résultante de ces trois forces si le point concidéré se déplace suivant une trajectoire rectiligne, en passant du point  au point
au point  .
. - On donne les sommets
 d’un quadrilatère. Démontrer que ses diagonales AC et BD sont perpendiculaires.
d’un quadrilatère. Démontrer que ses diagonales AC et BD sont perpendiculaires. - Déterminer la valeur de α pour laquelle les vecteurs
 et
et  sont perpendiculaires.
sont perpendiculaires. - Calculer le cosinus formé par les vecteurs
 et
et  .
. - On donne un triangle de sommets
 . Déterminer l’angle interieur au sommet B.
. Déterminer l’angle interieur au sommet B. - On donne un triangle de sommets
 . Déterminer l’angle interieur au sommet A.
. Déterminer l’angle interieur au sommet A. - Calculer la projection du vecteur
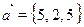 sur le support du vecteur
sur le support du vecteur  .
.
15. On donne trois vecteurs:  . Calculer
. Calculer  .
.
- On donne trois vecteurs:
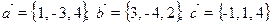 . Calculer
. Calculer  .
. 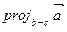 .
. - On donne trois vecteurs:
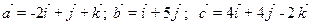 . Calculer
. Calculer 
 .
. - On donne les points:
 . Calculer
. Calculer  .
.
Réponses
1. 1) -6; 2) 9; 3) 16; 4) 13; 5) -61; 6) 37; 7) 73.
2. 1) -62; 2) 162; 3) 373.
3.  .
.
4. 1) 22; 2) 6; 3) 7; 4) -200; 5) 129; 6) 41.
5. 17.
6. 1) -524; 2) 13; 3) 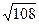 ; 4) {-70, 70, -350} et {-78, 104, -312}.
; 4) {-70, 70, -350} et {-78, 104, -312}.
7. 31.
8. 13.
10.  .
.
11.  .
.
12. 45°.
13. 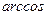 (
(  )
)
14. 6.
15. -4.
16. 5.
17. -11.
18. 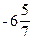 .
.
Date: 2016-03-03; view: 1072
| <== previous page | | | next page ==> |
| MY ATTITUDE TO LEARNING ENGLISH | | | Respuesta fisiológica del estrés |