
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
For the functions ; compute
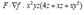
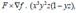


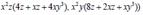
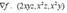
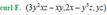

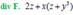
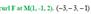
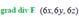
Formula of Integration by parts is: 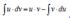
Formula that makes connection between definite and indefinite integrals is (Fundamental theorem): 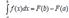
Gauss’s Formula: 

Green’s formula: 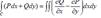
If¶A is a set of all boundary points ofn A Í R , then a closure of A is 
If3 f : [0,2p ]® R : t ® (cos t, sin t, t) and F(x, y, z) = (x, y, z), evaluate 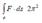
If3 ] 2 , 0 [ : R ® p f : t ® (cos t, sin t, t) and f(x, y, z) = x + y + z. Evaluate integral line 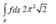
If a curve C is given by the parametrical equations x=x(t), y=y(t), z=z(t), a< t <b, and f is real valued
function, then 
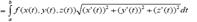
If the curve is given by explicit equation, then its arc length = 
If the curve is given by parametric equations, then its arc length = 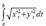
If the curve is given by polar equations, then its arc length = 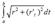
If x = r cos t cos u, y = r sin t cos u, z = r sin u, then Jacobean of this transformation = 
If x = r cos t, y = r sin t, then Jacobean of this transformation =r
If x = r cos t, y = r sin t, z = z, then Jacobean of this transformation = r
Let F(x, y) = (3xy,-y2), and C denote the path of y = 2x2 from (1, 2) to (0, 0). Evaluate 
Let F(x, y, z) = (2x – y + z, x + y - z2, 3x - 2y + 4z),and C denote the circle on the xy - plane with centre at the origin and radius 3, followed in the anticlockwise direction on the xy - plane. 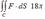
Let for 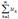 (un ≥ 0) the limit exist:
(un ≥ 0) the limit exist: 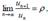 then a) the series converges ifr <1; b) the series diverges ifr > 1; c) the test fails ifr = 1. The test is known as: Ratio test
then a) the series converges ifr <1; b) the series diverges ifr > 1; c) the test fails ifr = 1. The test is known as: Ratio test
Let for 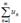 u (un ≥ 0) the limit exist:
u (un ≥ 0) the limit exist: 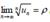 then a) the series converges ifr <1; b) the series diverges ifr > 1 ; c) the test fails ifr = 1. The test is known as: Root test
then a) the series converges ifr <1; b) the series diverges ifr > 1 ; c) the test fails ifr = 1. The test is known as: Root test
Let given two series: 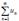 and
and 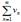 If for any n: un ≤ vn , then a) from convergence of
If for any n: un ≤ vn , then a) from convergence of 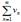 follows the convergence of
follows the convergence of 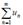 The test is known as: Comparison test
The test is known as: Comparison test
Let un= f (n) (f (n)ÎC and positive). Then the series  and the integral
and the integral  both are
both are
convergent or divergent. The test is known as: Integral test
Material point moves along the circle x = 2 cos t, y = 2 sin t in clockwise direction with the force F = (x + y)i – xj. Calculate work8p
Material point moves along the parabola y = - 3 x2 from the origin to the point (1, -3) with the force F = (x - y)i +2yj. Calculate work 10.5
Material point moves along the parabola y = x2 from the origin to the point (1, 1) with the force F = yi +(x+y)j. Calculate work 17/12
Open disc or open ball in Rn is 

Reduce the double integral to iterated integral : 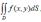 D -region is depicted
D -region is depicted
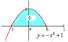

Reduce the double integral to iterated integral : 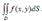 D -region is depicted
D -region is depicted 
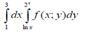
Reduce the double integral to iterated integral : 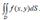 D -region is depicted
D -region is depicted

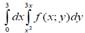
Reduce the double integral to iterated integral : 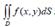 D -region is depicted
D -region is depicted

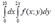
Reduce the double integral to iterated integral : 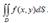 D -region is depicted
D -region is depicted


Solve equation:
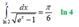
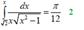
Sum of series: 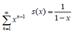
Suppose that  Evaluate
Evaluate 
Suppose thatm f : 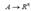 wheren A Í R . We say that
wheren A Í R . We say that 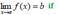
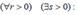
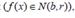
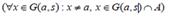
Take the indefinite integral:
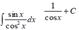

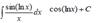
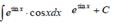

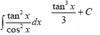

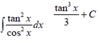
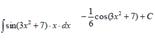
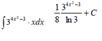
Test the function of two variables on extreme points:
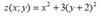

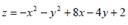
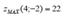
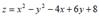

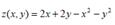

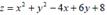
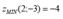
The length of the curve y = 𝐱𝟐 from x = 0 to x = 1 is (hint: length = 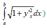
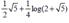
The length of the curve y = 𝐱𝟑/𝟐 from x = 0 to x = 4 is (hint: length = 
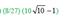
The length of the curve y = ln x from x = 3 to x = 8 is (hint: length = 

The length of the curve y = ln(1- x2) from x = 0 to x =1/2 is (hint: length = 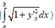 ln 3 - 1/2
ln 3 - 1/2
Date: 2016-03-03; view: 1736
| <== previous page | | | next page ==> |
| Find limit function of | | | CLOSE READING QUESTIONS |