Execution of the laboratory work

1. Study the rules of DL addition and subtraction.

2. Create subroutines of modulus calculation, addition, subtraction, and a generalized subroutine.

3. Input the subroutines into your computer.

4. Get results based on numerical data.

5. Compile your experimentation paper.

Contents of the Experimentation Paper

1. Principles of performing operations of addition and subtraction in the binary system and DL representation.

2. Algorithms of modulus calculation, addition, and subtraction.

3. Examples of calculations using a generalized program.

Questions for the Self-Testing

1. What are the basic differences between the addition algorithm in DL coding and that in the binary systems?

2. What are the causes of the subtraction error?

3. Compare the subtraction algorithm in complement code to the subtraction algorithm that uses borrowings.

MODULE 4

Laboratory work 4.1

REALIZATION OF DL MULTIPLICATION OPERATIONS

Aim of the work: The aim of the work is to study DL multiplication operations.

Basic Principles

The operation of multiplication is performed according to the bit-by-bit multiplication rule: N_i * N_k = N_i + N_k, where N_i and N_k are non-zero digits of the operands.

When two numbers A and B are being multiplied:

• each element of the number A is added to all elements of the number B;

• collecting terms is performed on a set of the obtained numbers of non-zero digits of the product;

• the product elements are sorted.

Example. Given: A→{0,2,2.1} and B→{0,2,3.1}. Their product is to be found. The partial sums are: {3.2} and {5.4}, i.e., {0,4,5.4.3.2}.

An error of multiplication may result from the limitations on the maximal value of resultant array elements and limitations on the size of this array. The size limitations are imposed at the last stage of performing the operation.

The flowchart of the MultDL subroutine for DL multiplication is depicted in Fig. 4.1. Here we use the following variables: a is an array of integers representing a DL multiplicand; b is an array of integers representing a DL multiplier; c is an array of integers representing a DL product; i, j, and l are cycles indices.

At first, the sign of the product is determined: c[0] = a[0] 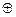b[0]. To multiply two operands a and b each element of the array a, beginning from the second one, must be added to each element of the array b, also beginning from the second one. This job is done in two cycles: one with a counter i, which is changed from 2 to a[1]+1 picking the corresponding elements from the array a, and the second one (enclosed in the first cycle) with a counter j, which is changed from 2 to b[1]+1 picking the corresponding elements from the array b. After the cycles have been completed, the product array c contains l elements that correspond to significant bits. The subroutine SORT sorts them and COL collects terms.

Date: 2016-03-03; view: 505