Isomorphism of graphs

The simple graphs 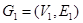and are isomorphic if there is a one-to-one and onto function f from V₁ to V₂ with the property that a and b are adjacent in G₁ iff f(a) and f(b) are adjacent in G₂, for all a and b in V₁. Such a function f is called an isomorphism. In other words, when two simple graphs are isomorphic, there is a one-to-one correspondence between vertices of the two graphs that preserves the adjacency relationship.

Example. Show that the graphs 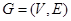and are isomorphic.

Solution: The function f with 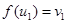, , 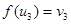and 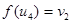is an isomorphism.

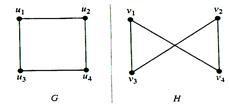
Example. Show that the graph G and H are not isomorphic.

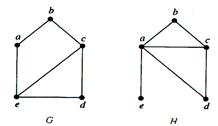
Solution: Both G and H have five vertices and six edges. However, H has a vertex of degree 1, namely e, whereas G has no vertices of degree 1. It follows that G and H are not isomorphic.

The number of vertices, the number of edges, and the degrees of the vertices are all variants under isomorphism. If any of these quantities differ in two simple graphs, these graphs cannot be isomorphic. However, when these invariants are the same, it does not necessarily mean that the two graphs are isomorphic.

Example. Determine whether the graphs G and H are isomorphic.

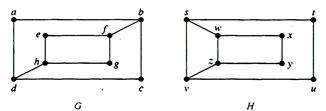
Solution: The graphs G and H have 8 vertices and 10 edges. They also both have 4 vertices of degree 2 and 4 of degree 3. Since these invariants all agree, it is still conceivable that these graphs are isomorphic. However, G and H are not isomorphic. To see this, note that since deg(a) = 2 in G, a must correspond to either t, u, x or y in H, since these are the vertices of degree 2 in H. However, each of these four vertices in H is adjacent to another vertex of degree 2 in H, which is not true for a in G.

To show that a function f from the vertex set of a graph G to the vertex set of a graph H is an isomorphism, we need to show that f preserves edges. One helpful way to do this is to use adjacency matrices. In particular, to show that f is an isomorphism, we can show that the adjacency matrix of G is the same as the adjacency matrix of H, when rows and columns are labeled to correspond to the images under f of the vertices in G that are the labels of these rows and columns in the adjacency matrix of G.

Paths

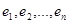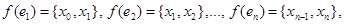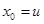A path of length n from u to v, where n is a positive integer, in an undirected graph is a sequence of edges of the graph such that where and 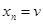. When the graph is simple, we denote this path by its vertex sequence 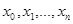(since listing these vertices uniquely determines the path). The path is a circuit if it begins and ends at the same vertex, that is, if u = v. The path or circuit is said to pass through or traverse the vertices 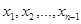. A path or circuit is simple if it does not contain the same edge more than once.

Example.

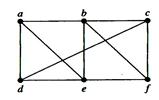
In this simple graph a, d, c, f, e is a simple path of length 4, since {a, d}, {d, c}, {c, f} and {f, e} are all edges. However, d, e, c, a is not a path, since {e, c} is not an edge. Note that b, c, f, e, b is a circuit of length 4 since {b, c}, {c, f}, {f, e} and {e, b} are edges, and this path begins and ends at b. The path a, b, e, d, a, b, which is of length 5, is not simple since it contains the edge {a, b} twice.

A path from a to b in a directed graph G is a sequence of one or more edges 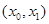, , 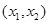, …, 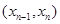in G, where 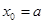and 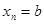, that is, a sequence of edges where the terminal vertex of an edge is the same as the initial vertex in the next edge in the path. This path is denoted by and has length n. A path that begins and ends at the same vertex is called a circuit or cycle.

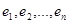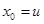A path of length n from u to v in a directed multigraph is a sequence of edges of the graph such that where and 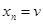. When there are no multiple edges in the graph, this path is denoted by its vertex sequence 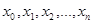. A path or circuit is called simple if it does not contain the same edge more than once.

Date: 2015-01-02; view: 1725