Sequential Quadratic Programming

http://vimeo.com/77448578

Most engineering optimization problems are not linear. To solve nonlinear problems, one approach is to repeatedly numerically approximate the problem as a locally linear one.

To do this, one can start a numerical search at a feasible point in 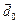in Rⁿ. At this point, one can numerically approximate the non-linear constraints by evaluating them at points around 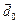, and fitting a linear surface to f, g, and h. Then, one can solve this linear problem as above with a fast simplex method for a new point 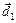.Then one can re-linearize the problem at 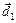, and so on, until it converges to a solution. This approach is called sequential linearization. In particular, sequential quadratic programming is a method whereby the constraints are linearized and the objective function is reduced to the nearest quadratic approximation.

Sequential quadratic programming is implemented as a tool in many software systems, such as spreadsheets and Matlab^TM.

Stopping Criteria

Given some numerical quantity to minimize over a search space, how do we know when we can stop the search? There are three answers to this question:

• When the separation in successive iterations becomes small:

This criterion is valid, but sometimes the function changes quickly, and so the prediction has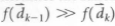

• When the difference in functional evaluations becomes small:

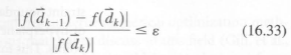
This criterion will define 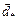as any point that is close enough; but sometimes the function might be very flat near 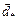, and so we might be placed very far away from 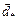as the agorithm slowly converges. Equation (16.33) must be checked to ensure [itself is not approaching zero (becomes less than e). If so, one can simply use the numerator. Generally, one should check both the relative and the absolute difference.

• When the difference in some arbitrary scalar function becomes small:

This criterion has use when we discuss constraints, since we might want to define a stopping criterion as a function of both the function we are minimizing and the constraint functions.

These definitions imply that we need an order of magnitude estimate of f, and we then choose e to be a few orders of magnitude less than this estimate.

Global Optimality

https://www.youtube.com/watch?v=Q_7aSByz90Y

The optimization methods presented in this chapter only determine a minimum over a restricted set. No guarantee is provided to determine a global optimum when there may exist many local optima. In general, global optimality, or numerically finding the best point over a domain, remains a research topic. Methods such as simulated annealing take a probabilistic approach, genetic algorithms apply domain splitting heuristics and searching heuristics.

https://www.youtube.com/watch?v=z1Cvn3_4yGo

Date: 2016-01-14; view: 840