Equality Constraints

The other general type of constraint we will use is an equality constraint. This type of constraint restricts certain design variables to be simultaneously related. We will denote equality constraints by h_j. We will also perform similar transformations on equality constraints h_j so they equal zero:

Note the reliance of all numerical constraints on the existence of a "zero." The algebraic structure of real valued numbers is intrinsically used to convert our previous "E" of Eq. (16.3) to a numerical "≤" statement.

Objective Functions

http://www.youtube.com/watch?v=J27r1QV7YOM

The performance metric feature we need, beyond constraints, is to identify an objective function. This objective will be the function we seek to minimize.

Definition.An objective function is a performance metric f we use to define to determine which configuration is better than all others, by minimizing f over D.

Standard Null Form

When we convert a product's performance metrics into constraints, g_j and h_j in the form as above, and select a single metric to serve as an objective function, we have cast the problem in a negative null form, the "null" signifying the zeros. If the ≤; on g were instead ≥, the problem is in positive null form. In this development, we will always use the negative null form.

This approach leads to the formulation of an optimization problem:

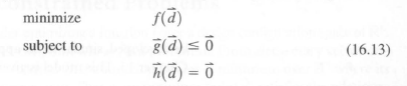
where 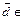D=Rⁿ, and all performance metrics are real valued. Any point 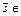D satisfying the constraints in Equation (16.13) is a feasible point, and all such points compose the feasible space S. This formulation of an optimization problem is called the standard null form of a nonlinear programming problem. The term "programming" arises historically. Whenever possible, we shall adopt this formulation. It is the clearest expression of the problem, one that can be readily encoded for evaluation by various algorithms and computer software.

Date: 2016-01-14; view: 767