A Basic Modeling Approach

To transform informal models into formal ones, we can consider a structured approach to modeling:

1. Identify a flow for the informal effect.

2. Identify a balance relationship for the flow.

3. Identify a boundary for the balance relationship.

4. Formulate an equation (or set of simultaneous equations) for the balance relationship in the system.

5. Use the resulting model to explore design configuration options.

STEP 1: Identify a Flow

We first identify a material, energy, or information flow associated with each effect of the product concept. This identification is a direct choice from the functional model of the product and overlaps with the preparation phase of product modeling.

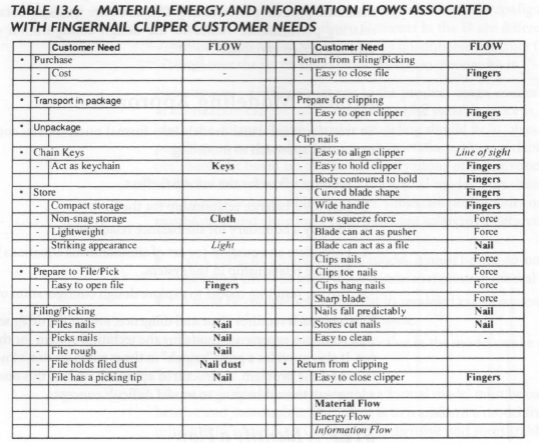
Example:Let's examine our customer-needs-to-flow diagram used to construct the function structure for a fingernail clipper product, as shown in Table 13.6.

Now let's choose a customer need (informal objective) to model, say "Easy to squeeze = Low finger force." The energy flow is "finger force," based on the function chain for the clipper, and the metric is "low finger force" as identified from benchmarking. Tracing finger force through the clipper, we have the representation shown in Figure 13.5. This representation helps us to develop a new fingernail clipper concept, understand its physics, and choose appropriate design parameter values to satisfy the customer needs.

The cutting motion acts like a scissors across the fingernail. A valid force flow is the force from the fingers, through the clipper, through the fingernail.

STEP 2: Identify a Balance Relationship

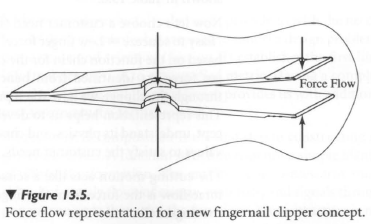
Having identified a material, energy, or information flow, we now must identify a balance relationship for the flow. Example: In the fingernail clipper, the forces above the cutting teeth must equal the forces below. The moments about the fulcrum must also sum to zero (assuming quasi-static analysis). The concept balance relationship is shown in Figure 13.6.

STEP 3: Identify the Boundaries

This step entails the recognition of the boundary conditions of the

product concept. How is it loaded, and how does it interact as a system with its environment (including the human interface)? What are the inputs and outputs across the boundaries, and what are the limits or ranges of these inputs and outputs?

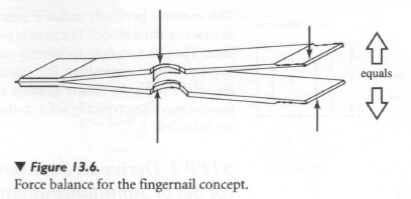
Example: In the fingernail clipper, it is profitable to model the forces by starting with the finger forces acting across the system boundary (Figure 13.7).

For this model, we could include the finger forces that are internal to the system and create a model of the forces through the finger, hand, and thumb. Such an approach is not necessary. We could zoom in on the cutting blades and not model the finger forces. Then we only have forces acting on the blades, which are not directly related to the forces required of the fingers. This approach is insufficient, since it does not capture the chosen product metric of finger force.

This example hopefully makes it clear how to select a proper level of abstraction for a model. The issue is pervasive to all engineering problems. The effect-to-flow-to-balance-to-system method is a reasonable approach-and generalizes. For example, fluid dynamics, heat transfer, solid mechanics (material stress and strain), and manufacturing process modeling typically use a control volume, and flows in and out are balanced.

STEP 4: Derive an Equation (or Set of Simultaneous Equations)

The next step involves converting the balance relationship to a mathematical form. This step is one of assigning geometric variables, material property constants, and others to formulate an equation (or set of simultaneous equations) that can be solved. The engineer's toolbox of applied mathematics and science is required here. In addition, a number of assumptions and simplifications will be required to develop a suitable model.

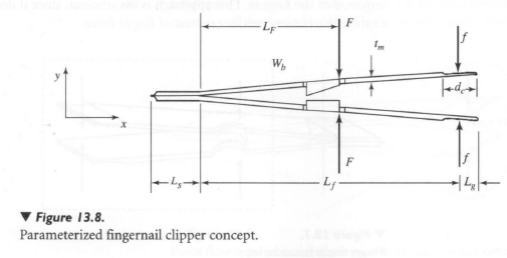
Example: Assigning dimension variables in the first control volume, the labeled fingernail clipper concept is shown in Figure 13.8. Summing moments about the fulcrum, the finger force required to actuate the clipper is:

The distances from the fulcrum to the force applications are design parameters (components of the D). The force F from the nail is unknown, however. We need to repeat the modeling process for the fingernail force, where we have a system of forces within a system of forces. To derive the force F, we model the fingernail being clipped. Figure 13.9 illustrates the fingernail force system.

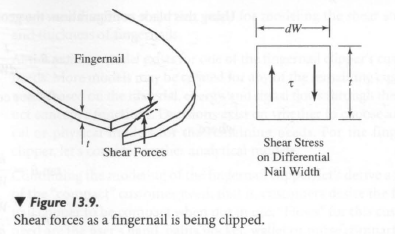
We may model the nail force as the shear stress over the nail cross-sectional area. Therefore:

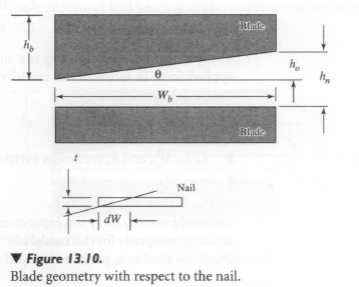
Now, how do we represent dW? Another system and model is needed. We can visualize that dW depends on the angle of the blade, as shown in Figure 13.10.

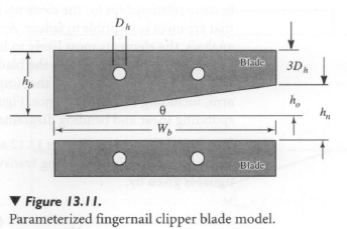
A balance relationship for the orthogonal coordinate system is the summation of individual feature distances along the fingernail clipper that must be added to a value that is less than a target value for the dimension. Considering this metric, a model of the clipper along the length (x) direction is given by Figure 13.8. Figure 13.11 provides additional geometry for modeling the height and width of the fingernail clipper.

VI. CONSTRUCTING PRODUCT MODELS: ADVANCED METHOD

http://www.youtube.com/watch?v=mmcK7oZ51ko

The previous section presents a basic model construction process as containing five fundamental steps. The focus of this process is to transform an informal description of product desires, obtained from earlier analysis, to a formal quantified model. Model preparation begins the process by establishing links of the informal description with product metrics. A functional model of the product concept, as well as the established architectural layout, provides additional links.

Functional models of a product concept relate material, energy, and information flows from the environment to the outputs produced by the product. These relationships, while informal, provide a basic structure for representing the underlying physics of the product's performance. This structure provides a solid foundation for incrementally building a formal analytical model. The chosen product metrics, in fact, are simply measures of the flows exiting functions in the product.

Approach

To build on the functional model foundation, transforming the informal models to formal ones, a systematic development approach is considered. Figure 13.22 shows an advanced modeling approach for product metrics, after Ashby (1992; 1987) and Beaumont (1998) and the previous discussion. It begins by considering the important effects (customer needs and associated engineering specifications), advances the model through physical mechanisms and interrogation, and ends with implementation of the model to explore alternative product configurations. Let's briefly examine the steps involved in this modeling approach.

Method

STEP 1: Identify the Effect (Customer Need/Engineering Specification)

We first contemplate what the model is for. Customer needs mapped to the main function carriers and then mapped to engineering specifications (metrics) is the essence of this step.

STEP 2: Identify a "Flow"

We next identify a material, energy, or signal flow associated with each customer need/metric of the product concept. This identification corresponds to the flows in the product's functional model. It may be used to understand the input-output transformation of the product in the sense of control volume analysis.

STEP 3: Identify the Physical Mechanisms

But how is the identified flow converted to a desired state by the product? How will the environment affect this transformation? We begin to answer these questions in this step. Physical principles must be listed that govern the product functions.

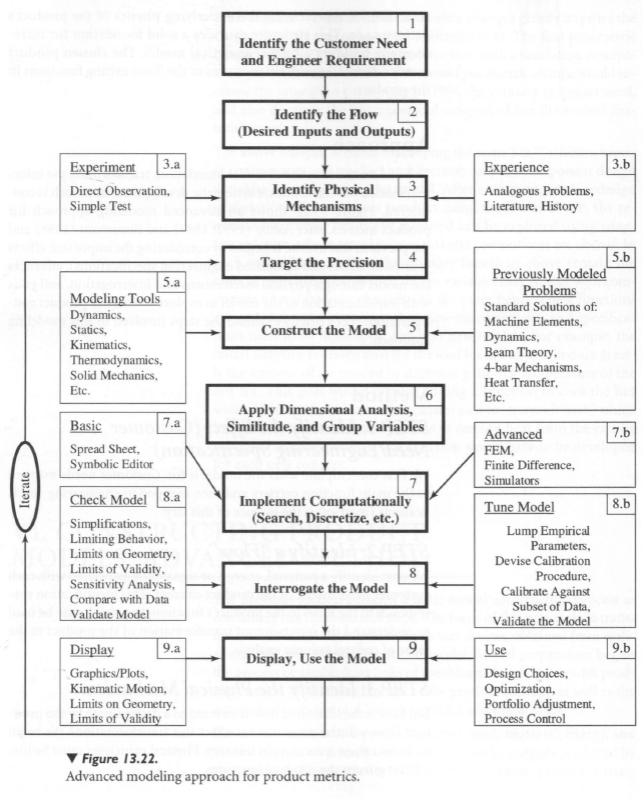
STEP 4: Target the Precision

With the metrics, flows, and physical mechanisms identified, the required precision of the model must be established. The precision must be chosen so that the model will produce effective results to make design decisions. Usually a percentage of the target values for the product metrics is used to set the precision of the product model.

STEP 5: Construct the Boundary and Balance Relationship

This step entails the establishment of system boundaries and the derivation of balance relationships that represent governing physical mechanisms. Basic mechanics from a variety of fields may be called on to create these balance relationships, equations, and boundary representations. It is also expected that the targeted precision is continuously referenced so that simplifications and assumptions may be made and justified (or not). This step concludes with an integration of all balance relationships and boundary conditions as a set of simultaneous equations or equivalent representation.

STEP 6: Apply Similitude/Dimensional Analysis

It is always a good idea to manipulate analytical product models into appropriate groups of dimensionless parameters whenever possible. Dimensionless parameters provide "scale lengths" for understanding the models and obtaining physical insights and trends. They also minimize problems encountered with unit conversions.

STEP 7: Embody the Model Computationally

The model should be converted to a computational form. This form may entail detailed finite element or difference models or other simulations. Alternatively, it may entail the simple coding of formulas in a spreadsheet or symbolic analysis. In either case, a computational form will provide a useful model for interrogation and design application.

STEP 8: Interrogate the Model

Once a model is constructed and integrated, it must be simplified, verified, and tested for its limits. Physical tests and known first-order solutions (such as beam theory) provide a sound basis for model interrogation. A subset of physical data (more than one point) must be collected to calibrate and validate the model. Unknown constants and model order must be adjusted during the calibration to improve the predictive capability of the model.

STEP 9: Display and Use the Model

Following interrogation, calibration, and validation, the model is ready for use. The design parameters must be clearly identified and bounded (if not already done so). The range of possible design configurations is then explored, followed by focused experiments/physical models to verify design choices and to uncover physical phenomena not included in the model.

This nine-step process augments and supplements the basic method of modeling product metrics. It adds keys steps such as interrogation and calibration of a model. The next section develops examples using this methodology.

VII. SUMMARY AND "GOLDEN NUGGETS"

In this chapter, basic and advanced product modeling techniques are developed. These methods are cast in the light of model preparation, formal and informal models, and analytical versus physical models. They are also presented in the context of customer needs and functional modeling. This context ensures a level of consistency for all model construction activities.

After studying this chapter, it is hoped that the reader gains an appreciation for modeling and its power in product development. Modeling is the fodder that transforms concepts to the beginnings of reality, the glue that infuses our insights into the product reality, and the engineer's toolbox that we bring to bear on the challenges of product evolution. Product modeling thus should be our passion. Without modeling, our innovative ideas may be lost in the swamp of implementation and product fabrication. Other novel ideas may never be discovered due to a lack of knowledge and understanding of our product system. We should not model for the mere sake of modeling, but rather abstract a product concept to fulfill its potential.

"Golden nuggets" from this chapter include the following:

• Product models are abstractions of physical reality. As abstractions, they require creativity and perseverance, but they also simplify critical product decisions.

• Model preparation wields the product data generated in earlier phases of the development process. These data reduce modeling cycle times and help ensure valid metrics and physical understanding.

• When considering a model, there always exists a trade-off between analytical and physical models (prototypes). This trade-off, at the most basic level, comes down to model accuracy versus prototype expense, that is, "$$"!

• Informal models are abundant as product descriptions. From customer statements to graphical sketches, informal models describe the essence of what a product should be. It is the design team's challenge to formalize the informal descriptions so that repeatable and defendable product decisions may be made.

• Metrics, boundaries, and balance relationships form the core modeling concepts. These concepts transform a product concept to a parameterized form. Calibration and focused experiments extend this form to a useable framework.

• Product modeling applications add to our experience and modeling toolbox. We must ftle away this experience for future development of product models.

Date: 2016-01-14; view: 546